Surfacing Point Sets with Fast Winding Numbers
/Winding number of different regions inside and outside a mesh with self-intersecting and overlapping components.
In my previous tutorial on creating a 3D bitmap from a triangle mesh, I used the Mesh Winding Number to robustly voxelize meshes, even if they had holes or overlapping self-intersecting components. The Mesh Winding Number tells us “how many times” a point p is “inside” a triangle mesh. It is zero when p is outside the mesh, 1 if it is inside one component, two if it is inside twice, and so on, as illustrated in the image on the right. The Winding Number is an integer if the mesh is fully closed, and if there are holes, it does something reasonable, so that we can still pick an isovalue (say 0.5) and get a closed surface.
This is a very powerful technique but it is also very slow. To compute the Mesh Winding Number (MWN) for a given point p, it is necessary to evaluate a relatively expensive trigonometric function for each triangle of the mesh. So that’s an O(N) evaluation for each voxel of an O(M^3) voxel grid. Slow.
The original Winding Number paper by Jacobson et al had a neat trick to optimize this evaluation, which takes advantage of the fact that if you are outside of the bounding box of an “open” patch of triangles, the summed winding number for those triangles is the same as the sum over a triangle fan that “closes off” the open boundary (because these two numbers need to sum to 0). We can use this to more efficiently evaluate the winding number for all the triangles inside a bounding box when p is outside that box, and this can be applied hierarchically in a bounding-box tree. This optimization is implemented in DMeshAABBTree3.WindingNumber(). However, although this gives a huge speedup, it is not huge enough - it can still take minutes to voxelize a mesh on a moderately-sized grid.
At SIGGRAPH 2018, I had the pleasure to co-author a paper titled Fast Winding Numbers for Soups and Clouds with Gavin Barill, Alec Jacobson, and David Levin, all from the University of Toronto’s DGP Lab, and Neil Dickson of SideFX. As you might have gathered from the title, this paper presents a fast approximation to the Mesh Winding Number, which also can be applied directly to surface point sets. If you are interested in C++ implementations, you can find them on the paper’s Project Page. In this tutorial I will describe (roughly) how the Fast Winding Number (FWN) works and how to use the C# implementation in my geometry3Sharp library, which you can find on Nuget or Github.
[Update 09-26-18] Twitter user @JSDBroughton pointed out that in the above discussion I claim that the Winding Number is an integer on closed meshes. This is true in the analytic-math sense, however when implemented in floating point, round-off error means we never get exactly 0 or 1. And, the approximation we will use below will introduce additional error. So, if you want an integer, use Math.Round(), or if you want an is-this-point-inside test, use Math.Abs(winding_number) > 0.5.
Fast Winding Number Approximation
The key idea behind the Fast Winding Number is that if you are “far away” from a set of triangles, the sum of their individual contributions to the overall mesh winding number can be well-approximated by a single function, ie instead of evaluating N things, you evaluate 1. In the Mesh Winding Number, the contribution of each triangle is it’s solid angle measured relative to evaluation point p. The figure on the right illustrates what the solid angle is - the area of the projection of the 3D triangle onto a sphere around p, which is called a spherical triangle.
When p is relatively close to the triangle, like in the figure, then any changes to the 3D triangle will have a big effect on this projected spherical triangle. However, if p is “far away” from the triangle, then its projection will be small and changes to the triangle vertices would hardly change the projected area at all. So, when the triangle is far away, we might be able to do a reasonable job of numerically approximating its contribution by replacing it with a small disc. In this case, instead of a 3D triangle we would have a point, a normal, and an area.
Of course, replacing an O(N) evaluation of triangles with an O(N) evaluation of discs would not be a big win. But, once we have this simplified form, then through some mathematical trickery, the spherical angle equation can be formulated as a mathematical object called a dipole. And the sum of a bunch of dipoles can be approximated by a single dipole, if you are far enough away. The figure on the right, taken from the paper, shows a 2D example, where the sum of 20 dipoles is approximated by a single stronger dipole. Even at relatively small distances from the cluster of dipoles, the scalar field of the sum is hardly affected by replacing the simplification.
This is how we get an order-of-magnitude speedup in the Winding Number evaluation. First we compute an axis-aligned bounding volume hierarchy for the mesh. Then at each internal node of the tree, we find the coefficients of a single dipole that approximate the winding number contributions for each triangle below that node. When we are evaluating the Winding Number later, if the evaluation point p is far enough away from this node’s bounding box, we can use the single-dipole approximation, otherwise we recursively descend into the node. Ultimately, only the triangles very near to p will actually have their analytic solid angles evaluated. The speedups are on the order of 10-100x, increasing as the mesh gets larger. It is…super awesome.
Also, since the dipole is a function at a point, we can apply this same machinery to a set of points that are not connected into triangles. We will still need a normal and an “area estimate” for each point (more on that below). But the result will the a 3D scalar field that has all the same properties as the Mesh Winding Number.
Mesh Fast Winding Number
There really isn’t much to say about using the Mesh Fast Winding Number. Instead of calling DMeshAABBTree3.WindingNumber(), call FastWindingNumber(). They behave exactly same way, except one is much faster, at the cost of a small amount of approximation error. Note that the internal data structures necessary to do the fast evaluation (ie the hierarchy of dipole approximation coefficents) are only computed on the first call (for both functions). So if you are planning to do multi-threaded evaluation for many points, you need to call it once before you start:
DMeshAABBTree3 bvtree = new DMeshAABBTree3(mesh, true);
bvtree.FastWindingNumber(Vector3d.Zero); // build approximation
gParallel.ForEach(list_of_points, (p) => {
double winding_num = bvtree.FastWindingNumber(p);
});There are a few small knobs you can tweak. Although the paper provides formulas for up to a 3rd order approximation, the current g3Sharp implementation is only second-order (we don’t have a third-order tensor yet). You can configure the order you want using the DMeshAABBTree3.FWNApproxOrder parameter. First order is faster but less accurate. Similarly, the parameter DMeshAABBTree3.FWNBeta controls what “far away” means in the evaluation. This is set at 2.0, as in the paper. If you make this smaller, the evaluation will be faster but the numerical error will be higher (I have never had any need to change this value).
Point Fast Winding Number
geometry3Sharp also has an implementation of the Fast Winding Number for point sets. This involves several interfaces and classes I haven’t covered in a previous tutorial. The main class we will need to use is PointAABBTree3, which works just like the Mesh variant. However, instead of a DMesh3, it takes an implementation of the IPointSet interface. This interface just provides a list of indexed vertices, as well as optional normals and colors. In fact DMesh3 implements IPointSet, and works fine with “only” vertices. So we can use a DMesh3 to store a point set and build a PointAABTree3, or you can provide your own IPointSet implementation.
To test the Point Fast Winding Number implementation, we will use a mesh of a sphere. Here is a bit of sample code that sets things up:
Sphere3Generator_NormalizedCube gen = new Sphere3Generator_NormalizedCube() { EdgeVertices = 20 };
DMesh3 mesh = gen.Generate().MakeDMesh();
MeshNormals.QuickCompute(mesh);
PointAABBTree3 pointBVTree = new PointAABBTree3(mesh, true);Now, I mentioned above that each point needs a normal and an area. We computed the normals above. But the per-point areas have a big effect on the resulting iso-surface, and there is no standard “right way” to compute this. In this case, since we know the point sampling of the sphere is approximately regular, we will assume the “area” of each point should be a disc around it, with radius equal to half the average point-spacing. Here is a way to calculate this:
double mine, maxe, avge;
MeshQueries.EdgeLengthStats(mesh, out mine, out maxe, out avge);
Circle2d circ = new Circle2d(Vector2d.Zero, avge * 0.5);
double vtxArea = circ.Area;The way we tell PointAABBTree3 about the per-vertex area estimates is to provide an implementation of the lambda function FWNAreaEstimateF:
pointBVTree.FWNAreaEstimateF = (vid) => {
return vtxArea;
};Now we can call pointBVTree.FastWindingNumber(), just like the mesh version. Now, say you would like to generate a mesh surface for this winding number field. We can easily do this using the MarchingCubes class. We just need to provide an ImplicitFunction3d implementation. The following will suffice:
class PWNImplicit : BoundedImplicitFunction3d {
public PointAABBTree3 Spatial;
public AxisAlignedBox3d Bounds() { return Spatial.Bounds; }
public double Value(ref Vector3d pt) {
return -(Spatial.FastWindingNumber(pt) - 0.5);
}
}Basically all we are doing here is shifting the value so that when the winding number is 0, ie “outside”, the scalar field value is -0.5, while it is 0.5 on the “inside”, and 0 at our “winding isosurface”, where the winding number is 0.5. We have to then negate these values because all our implicit surface machinery assumes that negative == inside.
Finally, this bit of code will do the surfacing, like in our previous implicit surface tutorials. Note that here we are using a cube resolution of 128, you can reduce this for quicker, lower-resolution results. It is also quite important to use the Bisection root-finding mode. The default is to use linear interpolation, but because of the “shape” of the winding number field, this will not work (as is described in the paper).
MarchingCubes mc = new MarchingCubes();
mc.Implicit = new PWNImplicit() { Spatial = pointSpatial };
mc.IsoValue = 0.0;
mc.CubeSize = pointSpatial.Bounds.MaxDim / 128;
mc.Bounds = pointSpatial.Bounds.Expanded(mc.CubeSize * 3);
mc.RootMode = MarchingCubes.RootfindingModes.Bisection;
mc.Generate();
DMesh3 resultMesh = mc.Mesh;The result of running this code is, as expected, a mesh of a sphere. Not particularly exciting. But the point is, the input data was in fact just a set of points, normals, and areas, and through the magic of the Point Fast Winding Number, we turned that data into a 3D isosurface.
Area Estimates and Scan Surface Reconstruction
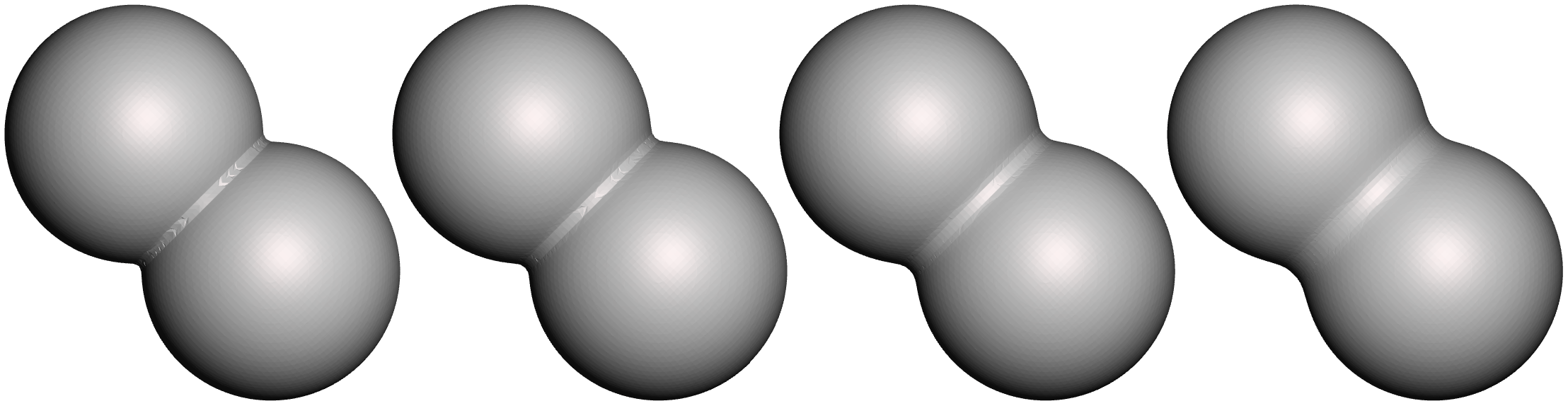
In the example above, we were cheating because we knew the point cloud came from a sphere, and specifically from a quite regular mesh of the sphere. This made it easy to get a sensible per-vertex area estimate. What if our estimate was not so good? An interesting experiment is just to scale our fixed per-vertex area. In the example below, we have the “correct” result on the left, and then the result with the area scaled by 2x, 4x, and 0.5x. The effects are neat, but also…not ideal for surface reconstruction.
Unfortunately there is no “right” way to assign an area to each point in a point cloud (in fact there is no “right” way to assign normals, either!). The Fast Winding Number paper describes a method based on using Delaunay Triangulations in local 2D planar projections around each point. This is a great way to do it, but it also involves several complicated steps, and can take quite a bit of time for a large point set. So, we’ll try something simpler below.
But first, we need a point set. For this test I will use a “real” point set, rather than a nice “synthetic” one that is sampled from a known triangle mesh. I am going to use the Chinese Dragon sample scan from the AIM@SHAPE 3D model repository. Actually I just used the “upper” scan, which contains 1,766,811 points, in XYZ format, which is a simple list of point positions and normals. You can directly open and view XYZ point cloud files Meshlab, a few screenshots are shown to the right. As you can see, the scan points are spaced very irregularly, and there are huge regions with no data at all! So, we cannot expect a perfect reconstruction. But if we could get a watertight mesh, then we can take that mesh downstream to tools where we could, for example, 3D sculpt the mesh to fix the regions where data was missing, take measurements for digital heritage applications, or just 3D print it.
Since the scanner provided (approximate) surface normals, the main thing we need to do is estimate an area for each point. This area clearly needs to vary per-point. We’ll try something just slightly more complicated than we did on the sphere - we’ll find the nearest-neighbour to each point, and use the distance to that point as the radius of a disc. The disc area will then be the point radius. Here’s the code:
DMesh3 pointSet = (load XYZ file here...)
// estimate point area based on nearest-neighbour distance
double[] areas = new double[pointSet.MaxVertexID];
foreach (int vid in pointSet.VertexIndices()) {
bvtree.PointFilterF = (i) => { return i != vid; }; // otherwise vid is nearest to vid!
int near_vid = bvtree.FindNearestPoint(pointSet.GetVertex(vid));
double dist = pointSet.GetVertex(vid).Distance(pointSet.GetVertex(near_vid));
areas[vid] = Circle2d.RadiusArea(dist);
}
bvtree.FWNAreaEstimateF = (vid) => {
return areas[vid];
};Note that this is not the most efficient way to compute nearest-neighbours. It’s just convenient. Now we can run the MarchingCubes surfacing of the Point-Set Winding Number Field defined with these areas. The result is surprisingly good (I was, in fact, literally surprised by how well this worked - the first time, no less!). The images below-far-left and below-far-right show the raw Marching Cubes output mesh, at “256” resolution. There is some surface noise, but a Remeshing pass, as described in a previous tutorial, does a reasonable job of cleaning that up (middle-left and middle-right images). The only immediately-obvious artifact of the dirty hack we used to estimate surface areas seems to be that in a few very sparsely sampled areas (like the rear left toe) the surface was lost.
In areas where there were no surface points, the winding field has produced a reasonable fill surface. I can’t quite say “smooth” because one artifact of the Fast Winding Number approximation is that in the “far field”, ringing artifacts can be visible. This is an artifact of using a hierarchical evaluation of a functional approximation. At each point in space we have to make a decision about whether to use a finer approximation or not, and this decision varies over space. (One potential fix here would be to smoothly transition or“blend” between approximations at different levels, instead of picking one or the other - something for a reader to implement?)
Summary
Traditionally, determining point containment for an arbitrary 3D mesh has been problematic to use in many applications because there wasn’t a great way to compute it. Raycast parity-counting is not efficient and can go horribly wrong if the mesh has imperfections, and voxelizing is memory-intensive and similarly fails on many real-world meshes. The Mesh Winding Number provides a much better solution, and the Fast Winding Number approximation makes it practical to use, even on huge meshes at runtime.
For example I have encountered many situations in building VR user interfaces where I want to be able to check if a point (eg on a spatial controller) is inside a 3D UI element (eg for selection). In most cases I would need to approximate the UI element with simpler geometric bounding-objects that support analytic containment tests. With the Fast Winding Number, we can now do these tests directly on the UI element.