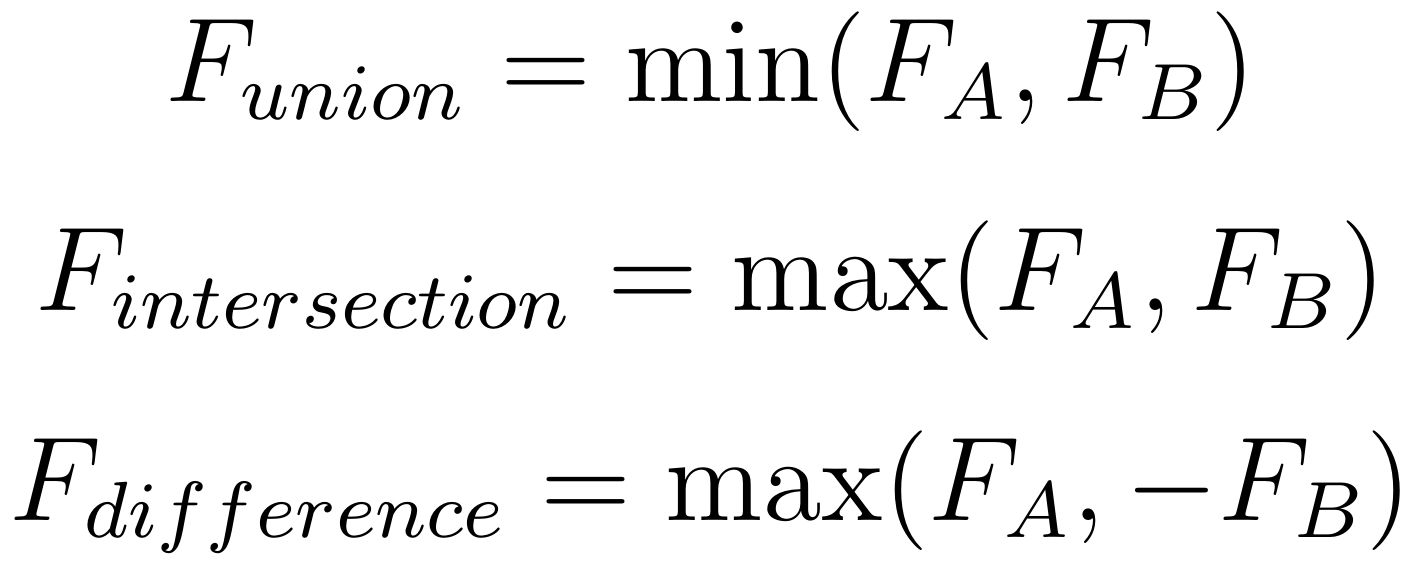The Tragic Tale of FTransform

If you spend any serious time trying to assemble scenes in Unreal Engine, you probably have run run across strange transform behaviors that occur when you have any kind of hierarchy of Components in an Actor. For example say you have a Wall mesh, and a Door mesh, maybe some Windows, and so you create a Blueprint that combines them into a single Actor that you can drop in wherever you need it. And then, perhaps, you think “oh I’d like the wall to just be a little bit taller in this spot” and you try to scale it up in Z. And something odd happens…

Many users, upon first encountering this situation, think “oh what a weird bug” and move on. And then later, after running into this problem for the Nth time, they start to think “this bug is getting annoying”. Maybe they file a bug report. Or maybe they work at Epic, and can repeatedly harass the Geometry Fellow (ie, formerly me) on Slack, with increasingly urgent requests for this “bug” to be “fixed”.

The problem, though, is that this behavior is not a bug. This behavior is by design. It’s baked into the core math code that implements 3D transforms in Unreal Engine, namely FTransform. It can’t just be “fixed” - if the math that results in this behavior was changed, it would quite likely break most UE projects. An enormous volume of C++ and Blueprint code is (inadvertently) dependent on this behavior. And one can even make a case that this weird behavior is an acceptable trade-off, in this game-engine context.

But what’s going wrong? Let’s investigate…

Hierarchical Geometric Transforms

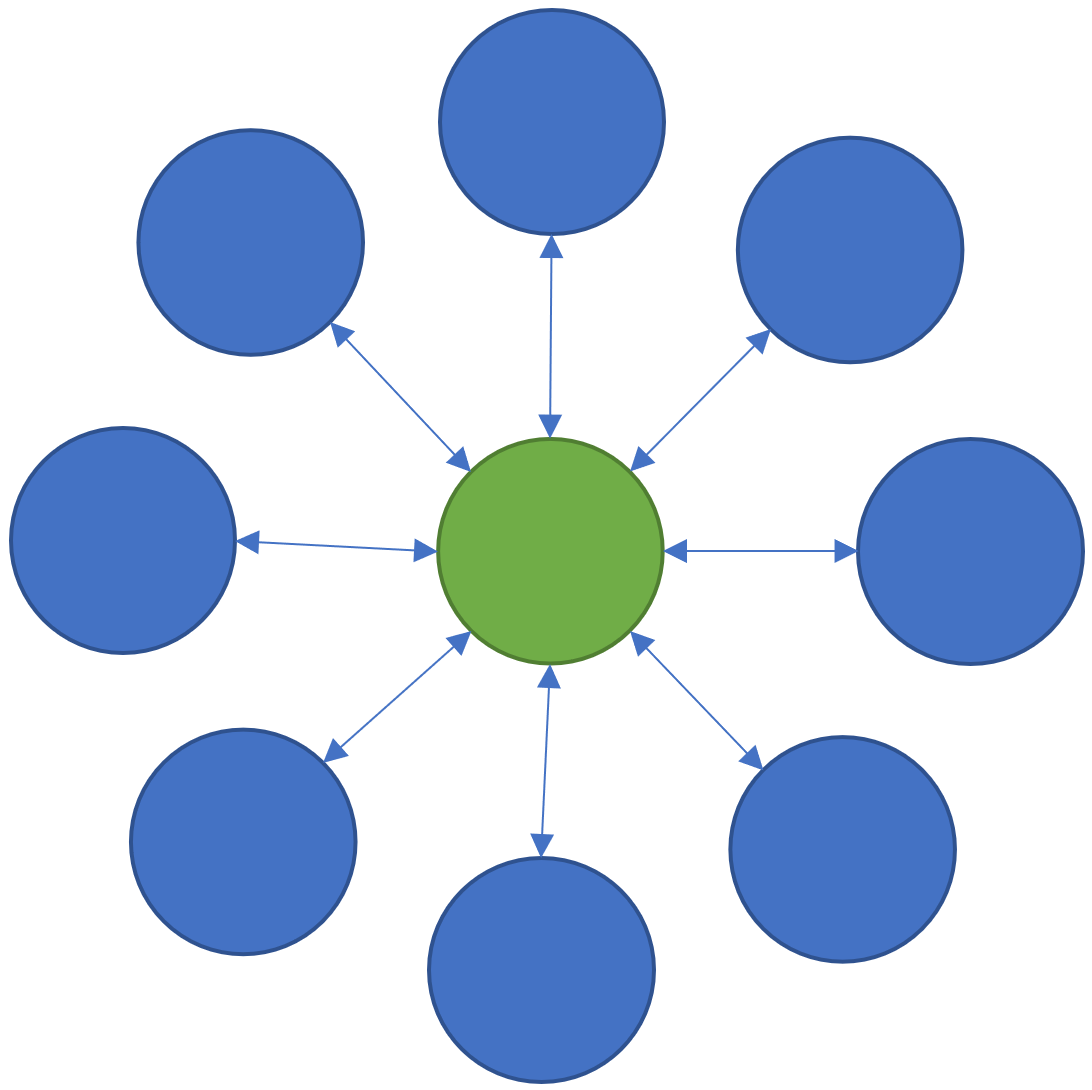
If you have a taken a Computer Graphics class in university, or skimmed a computer graphics textbook, you probably have come across the concept of “Hierarchical Modeling” or “Hierarchical Transformations”. The basic idea here is that you want to define the position of some object B relative to some object A using a geometric Transformation - for example a combination of Translation, Rotation, and Scaling. And then you might attach an object C to B via another Transformation, and so on, building up a tree of geometric relationships between parent and child objects.

Each of these Transforms defines a geometric mapping from the “local” space of an object and it’s parent. So on the right, if we want to know the location of a local-space point on object C in the “World” space, we first apply transformation Tcb, then Tba, then finally Tworld. And we can go from World to any Local Space by applying inverse-transformations.

The advantage of creating models with Transform Hierarchies is that if you want to transform the entire assembly in the World - ie move it to a new location, rotate it, resize it, and so on - you can do all that by manipulating Tworld. And similarly you can animate any branch of the Hierarchical Model by changing the Transform above the base of that branch.

Every 3D tool implements some kind of Transform Hierarchy. Generally the entire scene can be thought of as one huge hierarchical model, and “scene file formats” like GLTF and USD are based on precisely that structure. And most of them ultimately define the Transformations via the exact same math you will find in your Computer Graphics textbook - 4x4 Homogeneous Transformation Matrices. The reason for this is that if you have Tcb and Tba defined as 4x4 matrices, then you can combine them (via matrix multiplication) into a new single transformation Tca that maps directly from C to A, and is perfectly equivalent to doing it in two separate steps. I won’t explain this in any further detail, but here are some online textbooks [1] [2] and videos [3] on the topic.

A level in Unreal Engine also has a Transform Hierarchy - each Actor has a Transform that defines it’s position/rotation/scale in the level, and each Actor can contain multiple Components with some hierarchical parent/child arrangement, and any Component in this hierarchy with a geometric representation in the level (a USceneComponent) has a Transform. And this Transform Hierarchy behaves as you might expect if you came from some other DCC tool like Blender or Maya…that is, as long as you never non-uniformly scale anything.

FTransform

To understand what is going wrong in my wall example above, we need to look into how Unreal implements geometric transforms. Unreal does not use 4x4 Homogeneous Transformation Matrices. Instead FTransform stores 3 parts of a standard transformation separately. There is a Vector3 for Translation, a Quaternion (FQuat) for Rotation/Orientation, and then another Vector3 for Scaling. And if you look at the code for, eg, TTransform<T>::TransformPosition() in the file TransformNonVectorized.h, you will find that these 3 parts are applied as follows:

return Rotation.RotateVector( Scale3D * Point ) + Translation

So given a 3D Point in the “Local” space of the Transformation, that point is first Scaled, then it is Rotated, and finally it is Translated. The first thing you might note, if you are familiar with 3D transformations, is that this formulation does not include Shearing. Most 3D tools do not directly expose Shear transformations in their UI or 3D widgets, shears are only created indirectly. So at first glance, this seems like a minor limitation...(foreshadowing!)

Fundamentally what this formulation means is that the local coordinate space (and so the points inside it) can only be Scaled and Rotated around the local-space Origin (ie the (0,0,0) point). Once the Scaling and Rotation about the Origin is applied, then the Origin (and hence all points) are Translated.

Composing FTransforms

The issue arises when we try to combine two FTransforms A and B. If we apply them sequentially, ie B.TransformPosition( A.TransformPosition( P )), things will work as expected. However what if we want to combine A and B into a single FTransform C? In this case we have a Translation/Rotation/Scale from A, and also from B, and we need to construct a single new Translation Vector3, Rotation FQuat, and Scale Vector3 for the new FTransform C. Below I’ve written out the two transforms A and B in a slightly more mathy form, where the dot means “apply this transformation” (ie some kind of multiplication). The third line is the composed transformation from above, and the fourth is where we need to get, FTransform C.

So clearly what we are going to need to do is somehow turn the pairs of Rotations, Scales, and Translations in the third row, into single Rotations, Scales, and Translations in the fourth row. We can apply a standard rule of matrix math, namely that M•(A+B) = M•A + M•B, to rewrite the middle row as follows

The whole right side above, everything after the first +, ends up being a single Vector3, which is our new Translation component. So we’ve solved 1/3 of the problem. And we’ve grouped together the two Rotations and Scales on the left in a handy way, that makes it clear what we need to do. Two Rotations can be composed into a single Rotation, and two Scales can be multiplied together to define a new single Scale. So we can simply flip the order of Scale-b and Rotation-a, like I’ve done below, we can collect up the two R’s and the two S’s into the single Scale and Rotation for our new Transform C

Seems good, right? Unfortunately I have just committed a Math Crime, when I said “simply flip the order of Scale-b and Rotation-a” above. This “flip” is called commutation and in general, matrix multiplication is not commutative. You can’t just swap the order of a matrix multiplication. These aren’t technically matrices, they are quaternions and component-wise scaling vectors, but those are equivalent to a 3D rotation matrix and a 3D scale matrix. And if the Rotation and Scale matrices cannot commute, then neither can the Quaternion and Scale vector-multiplies.

If the scale is Uniform, then all 3 elements of the Scale Vector3 are the same. In this case, the Scale transformation or matrix is equivalent to a scalar multiplication - ie we can skip the matrix and just multiply the point by that single number. And the product of a scalar value and a matrix is commutative. So in the case of Uniform scaling, the reordering of terms above is valid, and we can construct the new FTransform C without any problems. Similarly if Rotation a or Scale b are the Identity matrix (ie no rotation or unit-scale), the respective terms disappear and we don’t have a problem. But outside these trivial cases, the flip is in question.

There are two special cases when matrices A and B commute. One is if both are diagonal, ie they only have non-zero elements along the matrix diagonal. This is the case for Scale matrices, but not for Rotations. The other is that if A and B are each symmetric, and their product is symmetric, then they commute. Rotation matrices are symmetric, and diagonal matrices are symmetric. However the product of a non-uniform scaling matrix and a Rotation matrix will not be symmetric except in the special case where the non-uniform scale is precisely aligned with the axis of rotation (which is why non-uniform scaling in a transform hierarchy sometimes works in UE - it depends on the Rotation!).

If you look at UE’s Transform/Transform composition code, in TTransform<T>::Multiply(), you’ll see that the combined Translation is defined exactly as I’ve done above. The composed Rotation and Scale are constructed as if the Scale is uniform, ie by simply combining the individual Rotation and Scale terms together into a new Rotation and Scale. Which, of course, doesn’t work mathematically if either Scale is non-uniform (most of the time).

So what happens, then?

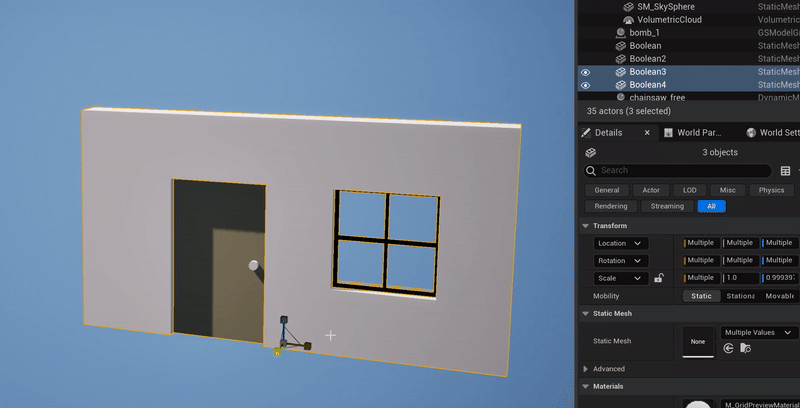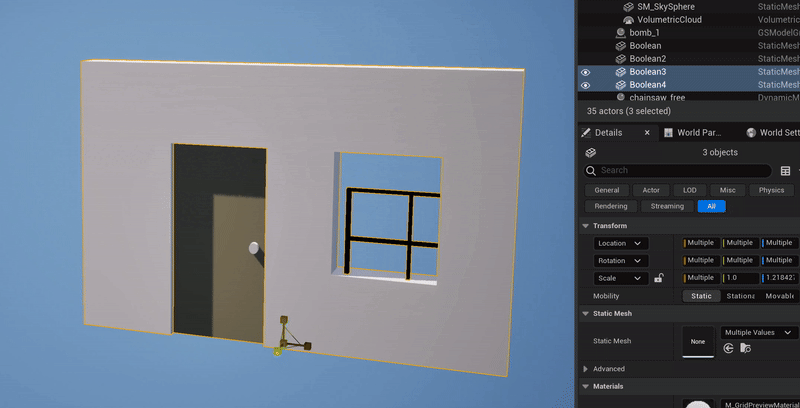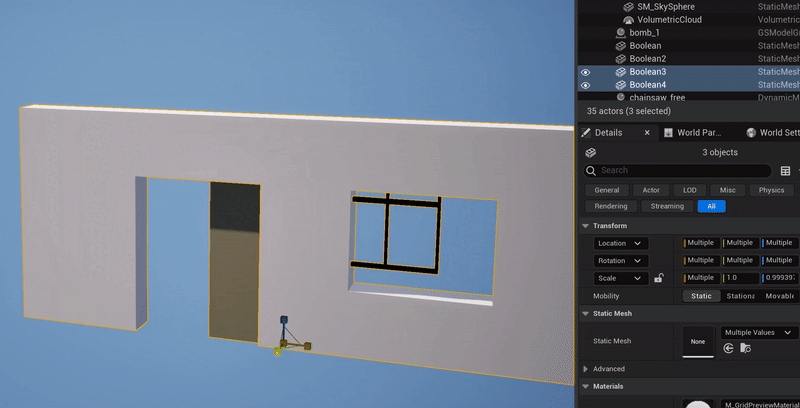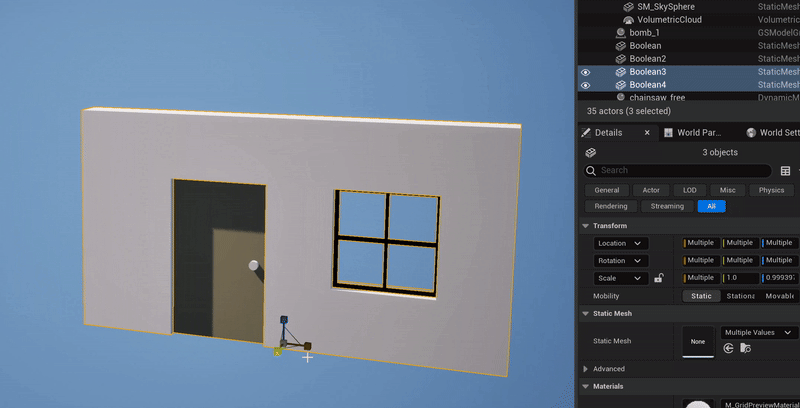
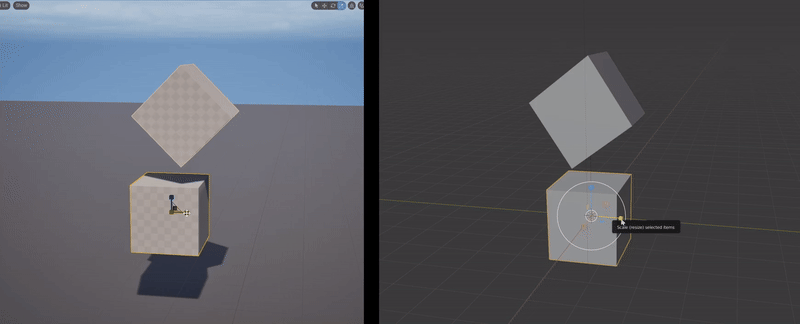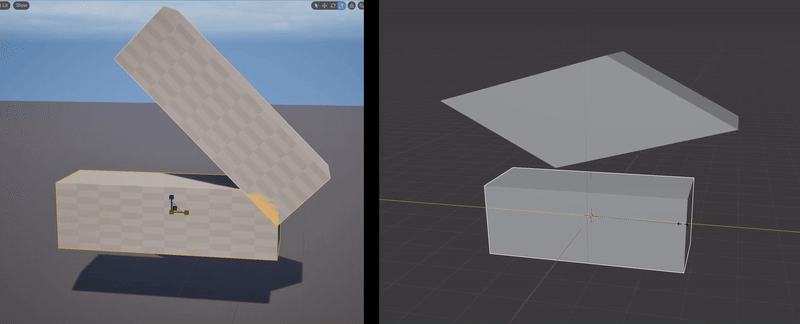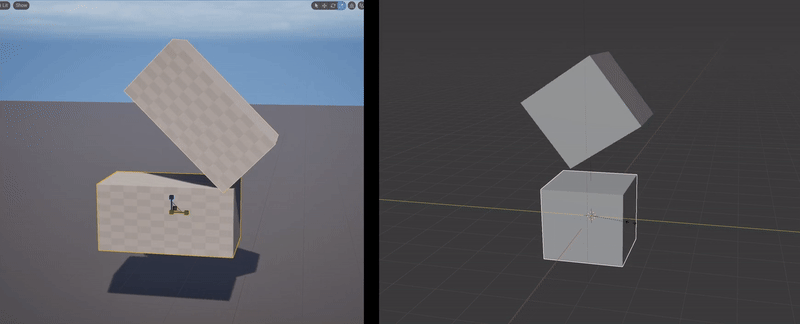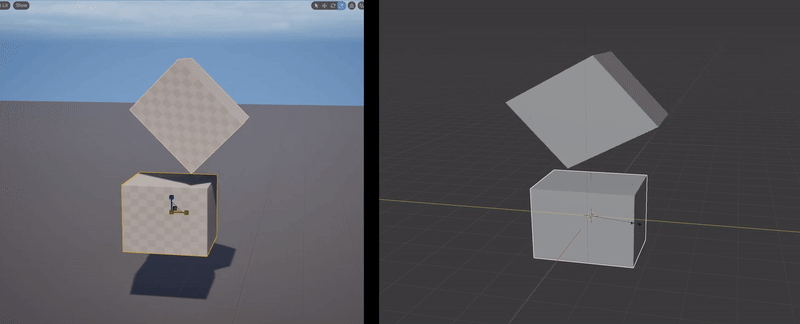
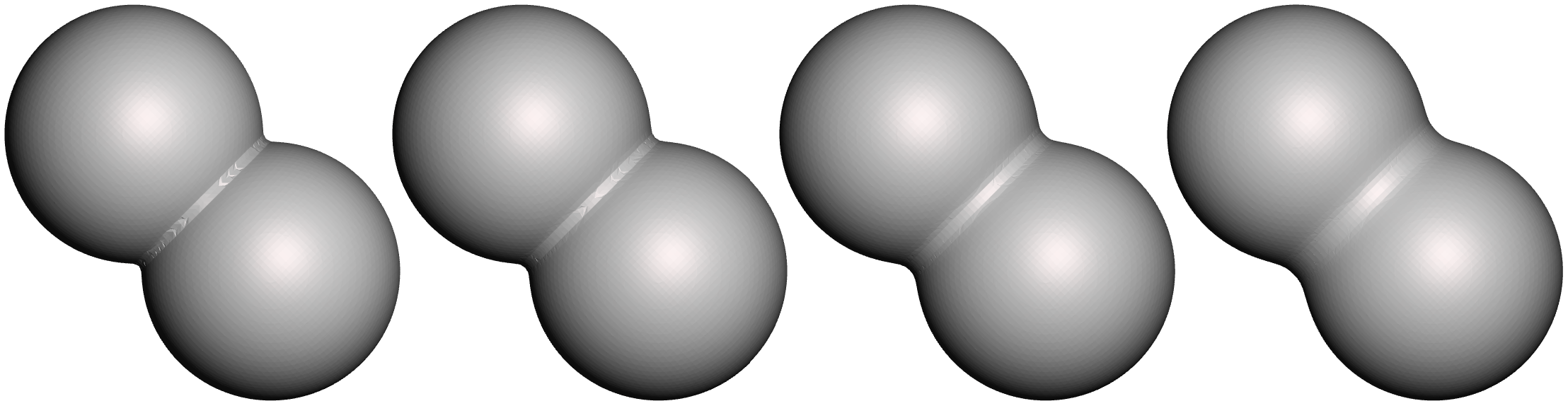
What happens when you illegally reorder and compose the non-uniform scaling & rotation parts of two FTransforms is, you get the wrong geometric transformation. The clip below-left shows a simple case where I have the upper box parented to the lower box, with a translation and 45-degree rotation, and I apply a non-uniform scale to the parent box. What happens is, the non-uniform scaling is “pushed down” into the local space of the child box. Effectively, the child object can only be non-uniformly scaled along the unit axes in it’s local coordinate system. A comparison with the behavior in Blender is shown on the right.

Blender’s behavior is “correct” in that the non-uniform scale along the unit X axis, when applied to a rotated box, should stretch the box in the unit-X direction. This transformation is not a Scale, it is a Shear. And this is the thing that FTransform can’t do - as I noted above, it doesn’t have a component for Shearing. There is no way to use or abuse it’s various terms that would result in a Shear transformation. And so producing this “correct” behavior via FTransform is impossible.

Why do we need to combine FTransforms, anyway?

I mentioned above that if you evaluate the transforms in sequence - ie B.TransformPosition( A.TransformPosition( P )) - then everything will work just fine. In that case, we don’t need to re-order any matrices and no math laws are at risk of being broken. So you might think, a solution to this problem is to just never try to combine FTransforms - in places where you want to do that, make a little list of them instead.

The issue with doing this is that Unreal Engine is a Real Time Game Engine and having to evaluate an arbitrary list of Transformations is wildly more expensive than just evaluating one. Unreal’s FTransform is heavily optimized - I pointed you to TransformNonVectorized.h above, but your IDE might have shown you that in a normal Unreal build the code in this file is not used. The actual code is in TransformVectorized.h, which uses platform-specific vector-math CPU instructions (ie SSE and the like), because the performance of transform evaluation is critical. Replacing a single transform with a small list dramatically increases the cost of evaluating the transform, at minimum because now a loop is needed, and also possibly a heap allocation. All bad stuff that game developers don’t like.

The situation is even worse on the GPU, because to take advantage of “instanced rendering” (an optimization where drawing the same object in multiple places in the level is dramatically cheaper), only a single transform can be specified for each instance. So the transform hierarchies have to be collapsed into single transforms for rendering. Now, at the GPU level, FTransform does not exist and a 4x4 matrix (actually 4x3 in many cases) is used…pointing to one possible solution - we’ll come back to that later…

From a software engineering standpoint, it is also very inconvenient to not be able to create single transforms that represent the local/world mapping for some geometric quantity. Transforms are generally assumed to be simple POD types because they frequently have to be passed around, copied, edited, and so on, and replacing all transform usage with transform-lists would be a major complication. So for all of these reasons, never combining FTransforms is a non-starter.

Do we really need Non-uniform Scaling?

Another potential workaround for this issue is to simply disallow non-uniform scaling. Because of the issues I demonstrated above, many UE users already avoid non-uniform scaling as a sort of tribal-knowledge rule-of-thumb. And many projects even try to enforce it as a sort of content-rule.

However one type of non-uniform scaling is virtually unavoidable in game development, and that is geometric Flips, ie to create a mirrored version of an object. Say you have a left-handed door and you need a right-handed variant. Making a fully separate asset is undesirable because (1) it means your game will need more memory and (2) it means you need to manage two Assets instead of one. If you have a car asset, you are not going to create separate left and right headlights, tires, seats, side-mirrors, and so on. You are just going to flip them. And so non-uniform scaling will find it’s way in there.

I noted above that if the non-uniform scaling is aligned with the axis of rotation, the matrix re-ordering is sometimes valid. This does often occur when constructing assets with flips, which make things appear OK…right up until someone says “maybe we could just tilt the headlights a bit” and then things suddenly go off the rails.

Why hasn’t UE switched to a 4x4 Matrix?

I mentioned above that at the Rendering level, FTransform is not used. And even the “interface” object that mediates between the scene Components and the Rendering level (called FPrimitiveSceneProxy) uses either an 4x4 FMatrix or a FRenderTransform (which is basically a 4x3, a minor memory optimization). So on first glance it does appear that FTransform is purely a legacy data format, that could conceivably be replaced. Yes, it would be incredibly painful, with enormous fallout (much more than the UE5 transition from float to double-precision “large world coordinates”!!). But not impossible.

However, something significant would be lost along the way. For starters, consider this little panel which you probably have used an enormous number of times:

In this UI, the rotation, scale, and translation members of FTransform are directly exposed. The Scale values here are simply the values of the Scale Vector3 in the FTransform, and there is a trivial direct mapping between the rotation angles and the FQuat. Now consider what happens when those three separate transforms are collapsed into a single 4x4 matrix. What values do we show in the UI panel? The matrix elements do not correspond to the fields - in particular the Scale and Rotation are mixed together in the upper 3x3 portion of the matrix.

To turn the 4x4 matrix back into separate Scale and Rotation, a decomposition algorithm must be used. It is, comparatively, very expensive to do this reverse-mapping via decomposition, compared to simply reading out the values of FTransform. And once we mix in non-uniform scaling, we may have introduced a shear transformation, as I mentioned above. This shear is highly problematic for decomposition algorithms, with the result that the rotation-angles boxes will have unpredictable behavior when trying to show values for a sheared transform (this can be observed in some more advanced DCCs like Maya, that implement this kind of decomposition strategy).

Now you might say “so what, having some weird UI dialog boxes is a small price to pay to avoid this significant problem”. I have even made that case myself, and in a modeling/animation DCC tool it’s an acceptable tradeoff. However Unreal is a game engine and that means that users are not just making (possibly animated) scenes via GUI panels - they are making those scenes interactive with code. And a huge amount of that code involves manipulating transform components - both reading and writing. It’s effectively the same problem as the UI boxes, except that instead of a person having to deal with the weirdness, it will be code…

For example a very common thing to do is to animate an object by, eg, reading it’s rotation angles every frame, adding a little delta, and updating the transform. A novice, non-mathematician can easily understand this kind of programmatic animation logic, and your average game includes an enormous amount of this kind of direct transform-component manipulation, often inside nested transform hierarchies. Similarly, the literal values of the FTransform are often read back and used to drive gameplay. A simple example would be something like a puzzle element where the player has to rotate an object until it points in a particular direction, which could be programmed by checking if the rotation angle is within a min/max interval.

Of course there are ways to the same kind of programmatic manipulations for 4x4 matrices - but they generally involve constructing a new transform to multiply with the current transform. And that construction can end up being quite complicated. In particular it can be quite difficult to encapsulate transform-manipulation logic because (eg) to rotate an object around it’s local up-axis, you are going to need to know how to construct that axis, instead of just knowing that you want to modify the already-cleanly-separated-out “Y” angle of it’s rotation component. These kinds of things are not difficult for a skilled geometer, but can be deeply frustrating for a novice indie game developer who has never taken a linear-algebra class.

So FTransform is (unfortunately) ideal for this kind of programmatic transform manipulation by non-math-experts. And that’s why we are likely stuck with it!

Implications for Scene Graphs like GLTF and USD

Although it may not be immediately obvious, the limitations of FTransform become highly problematic when it comes to trying to import entire Scene Graphs via formats like GLTF or USD. A complex scene created in a DCC tool that implements hierarchical transforms “correctly” can easily contain flips, non-uniform scaling transforms, or even explicit shear transforms, that are mathematically impossible to represent correctly in Unreal Engine.

The only way to resolve this is to “bake” the transformed vertex positions into sub-elements of the scene (which is what these importers tend to do). This avoids “breaking” the shape of geometric elements in the scene. However it also means that UE does not contain the same meshes or hierarchy as the source file, which greatly complicates any attempt to maintain a relationship between the source USD scene and the in-UE scene.

There are many challenges that are blocking the “dream” of having a bi-directional link between the UE scene graph and that of a USD file (and frankly I don’t think it’s a good idea anyway). However many of them are engineering “wow that would be a lot of work to build and maintain” limitations - this one is a fundamental math issue, as we have seen.

Thanks for Reading!

Do you have questions or comments? Please find your author on the gradientspace discord. And perhaps you would like to try the Gradientspace UE Toolbox plugin!

Unofficial Geometry Script & DynamicMeshComponent FAQ

Geometry Script(ing) is a Blueprint/Python (UFunction) library first released in Unreal Engine 5.0 that allows users to query and manipulate triangle meshes (and a few other geometric data types). I initially developed Geometry Script based on some previous public experiments I published on this website, specifically Mesh Generation and Editing at Runtime and Procedural Mesh Blueprints.

At time of writing, Geometry Script is an Experimental feature plugin in UE 5.1, which means it has pretty minimal documentation and learning materials. I have published a short series of tutorial videos on YouTube demonstrating how to use Geometry Script Blueprints for various tasks, see the playlist here. Geometry Script was also used heavily in the level design of the UE5 Lyra sample game, see documentation here.

As the main developer of Geometry Script, I get a lot of questions about how to use it, what it can do, etc. A lot of the same questions. So this page is (hopefully) a living document that I will update over time. Geometry Script is used primarily to modify UDynamicMesh objects, and the main way you access or render a UDynamicMesh is via DynamicMeshComponent / DynamicMeshActor. So, this FAQ will also cover some aspects of DynamicMeshComponent that frequently come up in the context of Geometry Scripting.

If you have questions this FAQ doesn’t answer, you might try posting on the Unreal Developer Community forums (https://dev.epicgames.com/community/), asking in the #geometry-scripting channel on the UnrealSlackers Discord ( https://unrealslackers.org ), or @ me on Mastodon (https://mastodon.gamedev.place/@rms80), or (still) Twitter (https://twitter.com/rms80). Note, however, that I strongly prefer to answer questions in public rather than in private/DM.

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games. However, gradientspace.com is his personal website and this article represents his personal thoughts and opinions. About triangles.)

Contents

(note: sorry, none of these are linked yet - soon!)

Basics

• Is there any documentation for Geometry Script at all?

• Does Geometry Script have a function for X?

• Is there a published Roadmap for Geometry Script?

• None of these Geometry Script functions show up for me in the Blueprint Editor

• Some functions are missing when I try to use them in my Actor Blueprint

• I can’t find the function “Event On Rebuild Generated Mesh” to override in my Actor Blueprint

• Does Geometry Script always run on the Game Thread?

• Can I run GeometryScript functions in a background thread or asynchronously?

• Is there any built-in support for running Geometry Script functions asynchronously?

• Can I run a Geometry Script Blueprint on the GPU?

• Does Geometry Script work with Skeletal Meshes?

• Does Geometry Script work with Landscape, Geometry Caches, Geometry Collections, Hair/Grooms, Cloth Meshes, or some other UE Geometry Representation?Is Geometry Script Deterministic? Are scripts likely to break in the future?

• Can I animate a mesh with Geometry Scripting? Can I implement my own skinning or vertex deformation?

Runtime Usage

• Can I use Geometry Script in my Game / At Runtime?

• Should I use DynamicMeshActors generated with Geometry Script in my Game?

• Will DynamicMeshComponent be as efficient as StaticMeshComponent in my Game?

• Why are all my GeneratedDynamicMeshActors disappearing in PIE or my built game ?!?

• Is GeometryScript function X fast enough to use in my game?

• How can I save/load Dynamic Meshes at Runtime?

• Can I use Geometry Script to modify Static Meshes in my Level at Runtime?

• The function “Copy Mesh From Static Mesh” is not working at Runtime

• The Mesh I get when using “Copy Mesh From Static Mesh” at Runtime is different than the mesh I get in the Editor

• The functions “Apply Displace from Texture Map” and/or “Sample Texture2D at UV Positions” are working in the Editor but not at Runtime

Rendering and UE Features

• Does DynamicMeshComponent support Nanite, Lumen, or Mesh Distance Fields?

• Does DynamicMeshComponent work with Runtime Virtual Texturing (RVT)?

• Does DynamicMeshComponent support Physics / Collision?

• DynamicMeshComponents don’t show up in Collision Debug Views!

• Does DynamicMeshComponent support LODs?

• Does DynamicMeshComponent support Instanced Rendering?

Lyra Sample Game

• How does the Non-Destructive Level Design with GeometryScript-based mesh generator “Tool” objects work in Lyra?

• How can I migrate the Lyra Tool system to my own project?

Basics

Is there any documentation for Geometry Script at all?

Yes! Here is a direct link into the UE5 documentation: https://docs.unrealengine.com/5.1/en-US/geometry-script-users-guide .

Several livestream and tutorial sessions have also been recorded. At UnrealFest 2022, the Introduction to Geometry Scripting session demonstrated how to create various Editor Utilities with Geometry Script, and during the Modeling and Geometry Scripting in UE: Past, Present, and Future session I gave a brief demo and some high-level context around Geometry Script. Earlier in 2022, I participated in an Inside Unreal livestream where I did some Geometry Scripting demos.

Does Geometry Script have a function for X?

This is often a difficult question to answer without more information. However, a relatively complete reference for all the current Geometry Script library functions is available in the UE5 documentation here: https://docs.unrealengine.com/5.1/en-US/geometry-script-reference-in-unreal-engine

Is there a published Roadmap for Geometry Script?

Currently there is not. Geometry Script is being actively developed and the most effective way to see what is coming in the next UE5 Release is to look at what commits have been made in the UE5 Main branch in the Unreal Engine Github. Here is a direct link to the Geometry Script plugin history: https://github.com/EpicGames/UnrealEngine/commits/ue5-main/Engine/Plugins/Experimental/GeometryScripting. Note that this link will not work unless you are logged into GitHub with an account that has access to Unreal Engine, which requires you to sign up for an Epic Games account (more information here).

None of these Geometry Script functions show up for me in the Blueprint Editor

You probably don’t have the Geometry Script plugin enabled. It is not enabled by default. The first video in my Geometry Script Tutorial Playlist on Youtube shows how to turn on the Plugin.

Some functions are missing when I try to use them in my Actor Blueprint

You are likely trying to use a function that is Editor-Only. Some functions like creating new Volumes or StaticMesh/SkeletalMesh Assets, and the Catmull Clark SubD functions, are Editor-Only and can only be used in Editor Utility Actors/Actions/Widgets, or GeneratedDynamicMeshActor BP subclasses.

I can’t find the function “Event On Rebuild Generated Mesh” to override in my Actor Blueprint

This event only exists in Actor Blueprints that derive from the GeneratedDynamicMeshActor class. It’s likely you are trying to find it in a generic Actor Blueprint, or in a DynamicMeshActor Blueprint.

Does Geometry Script always run on the Game Thread?

Currently Yes. Actor Blueprints and Editor Utility Blueprints are always executed on the Game Thread, and so the Geometry Script functions that are called also run on the Game Thread. Some Geometry Script functions will internally execute portions of their work on task threads, eg via C++ calls to ParallelFor, Async, or UE::Tasks::Launch(). However this will only occur in the context of a single function, and the function will not return until all that parallel work is completed.

Can I run GeometryScript functions in a background thread or asynchronously?

It is generally considered to be not safe to modify any UObject in a background thread. Geometry Script functions modify a UDynamicMesh, which is a UObject, and technically it is possible for a UObject to become unreferenced and garbage-collected at any time.

However, if in your specific use case you know that the UObject will not become unreferenced, then most(***) Geometry Script functions can safely be run in a background thread, as long as you don’t try to edit the same mesh from multiple threads. In my article on Modeling Mode Extension Plugins, I demonstrated taking advantage of this to build interactive mesh editing tools using Geometry Script that compute the mesh edit asynchronously.

The (***) above is because any Geometry Script function that touches an Asset, Component, or Actor (eg has any of those as input) cannot safely be run asynchronously.

Is there any built-in support for running Geometry Script functions asynchronously?

No, as of 5.1 there is not.

Can I run a Geometry Script Blueprint on the GPU?

No, this is not possible and won’t ever be. Geometry Script is a thin wrapper around a large C++ library of mesh processing algorithms and data structures. General-purpose C++ code cannot be run directly on a GPU. In addition, many of the mesh processing operations exposed in Geometry Script, like Mesh Booleans, involve complex queries and modifications over unstructured graphs where dynamic memory allocations are generally involved, which is the kind of computation problem that CPUs are much better at than GPUs.

Does Geometry Script work with Skeletal Meshes?

In 5.1 there is limited support for from a SkeletalMesh to a DynamicMesh and back, similar to the StaticMesh approach. However, how to automatically generate or update skin weights after complex mesh edits basically remains an unsolved problem in animation, and so procedural mesh edits done this way likely will not result in desirable skin weights.

Does Geometry Script work with Landscape, Geometry Caches, Geometry Collections, Hair/Grooms, Cloth Meshes, or some other UE Geometry Representation?

Not in UE 5.1. Nearly all Geometry Script functions only work with UDynamicMesh objects. There are functions to convert the internal mesh representations from Static and Skeletal Meshes, and Volume Actors, into a UDynamicMesh, and then functions to convert back. No such functions currently exist for these other geometry types.

Is Geometry Script Deterministic? Are scripts likely to break in the future?

Most functions in Geometry Script are deterministic. Several are not, however - in particular mesh simplification and remeshing functions currently may not produce the same mesh every time. In general, it is difficult to provide hard determinism and compatibility guarantees in procedural mesh generation systems, as things that are clear bugs or performance issues can change the result mesh when they are fixed/resolved. Deterministic versions of operations may also be slower, as in some cases the most efficient parallel-processing implementation produces non-determinism. Operations like a Mesh Boolean can have a huge dependency tree of geometric operations, and any change to one of them might affect the result. So the only way to ensure deterministic compatibility is to keep the “old” version of the code around, bloating the binary size (this is what CAD software generally does to ensure compatibility between versions).

Can I animate a mesh with Geometry Scripting? Can I implement my own skinning or vertex deformation?

This is technically possible, either by fully regenerating the mesh every frame, or by (for example) using Geometry Script to update the vertex positions of a DynamicMesh every frame. However, this is not a very efficient way to implement animation, and except for very simple examples (eg say a simple primitive shapes, basic mesh booleans, etc) is unlikely to provide acceptable runtime performance. Each time the DynamicMesh is regenerated or updated, a series of relatively expensive operations occur, including generating new vertex and index buffers and uploading them to the GPU (this GPU upload is often the most expensive part). Skinning in something like a SkeletalMesh is computed directly on the GPU and so is much, much faster.

However if you don’t need to update the deformation every frame, or don’t need realtime performance (ie for experimental or research purposes), Geometry Scripting may work for you. It is possible to (eg) iterate over all mesh vertices and update their positions, even for meshes with millions of vertices.

Runtime Usage

Can I use Geometry Script in my Game / At Runtime?

Mostly Yes. Some Geometry Script functions are Editor-Only, but the majority work at Runtime. Notable things that do not work at Runtime include creating new Volume actors, creating/updating Static or Skeletal meshes, and Catmull Clark SubD.

Should I use DynamicMeshActors generated with Geometry Script in my Game?

If your meshes are static in the Game, IE you just want the convenience of procedural mesh generation for in-Editor Authoring, then the answer is probably no. DynamicMeshComponent (the component underlying DynamicMeshActor) is relatively expensive compared to StaticMeshComponent (see below). You should almost certainly “bake” any generated DynamicMeshActors into StaticMesh/Component/Actors, that’s what we did in the Lyra sample game. I have a short tutorial video on doing so here.

If your meshes are dynamic, ie they need to be dynamically generated at Runtime, or modified in-Game, then the answer is probably yes. There are various other options like ProceduralMeshComponent, the third-party RuntimeMeshComponent which is quite good, and runtime-generated StaticMesh Assets. However none of these options has an internal UDynamicMesh that can be directly edited with Geometry Script.

Will DynamicMeshComponent be as efficient as StaticMeshComponent in my Game?

No. DynamicMeshComponent uses the Dynamic Draw Path instead of the Static Draw Path, which has more per-frame rendering overhead (there is a GDC talk on YouTube about the Unreal Engine Rendering Pipeline by Marcus Wassmer which explains the Static Draw Path optimizations for Static Meshes). DynamicMeshComponent does not support instanced rendering, so mesh memory usage is generally higher. And the GPU index/vertex buffers created by a DynamicMeshComponent are not as optimized as those in a cooked StaticMesh asset (really, really not as optimized).

In addition, the DynamicMeshComponent always keeps the UDynamicMesh memory available on the CPU - a cooked StaticMesh Asset usually does not. The FDynamicMesh3 class underlying UDynamicMesh also has a minimum size and grows in fixed “chunks” of memory, so (eg) a one-triangle DynamicMesh will consume quite a bit more memory than a comparable one-triangle StaticMesh’s FMeshDescription would.

Why are all my GeneratedDynamicMeshActors disappearing in PIE or my built game ?!?

GeneratedDynamicMeshActor is an Editor-Only subclass of DynamicMeshActor, meant for in-Editor procedural mesh generation. GeneratedDynamicMeshActor’s convenient “rebuild” system is usually not appropriate in a game context, where you likely need to more precisely manage when meshes are generated/etc. I have a short tutorial video here on how to set up a DynamicMeshActor that can be generated/edited at Runtime.

Is GeometryScript function X fast enough to use in my game?

Since Geometry Script works on Meshes, which have a variable number of triangles and vertices, the only answer anyone can ever give to this question is “you will have to try it and profile”. Any non-trivial function in Geometry Script is at least linear in the number of vertices/triangles, and many are more complex. For example the Mesh Boolean node must build an AABBTree for each of the two input meshes, then do relatively expensive pairwise-triangle intersection tests (based on the AABBTree traversal, which efficiently skips most non-intersections). If you have two basic cubes, this is quite fast. If you try to subtract a cube every frame, the mesh will accumulate more and more triangles over time, and the Boolean will become increasingly expensive.

How can I save/load Dynamic Meshes at Runtime?

Unreal Engine doesn’t provide any built-in mesh load/save system at Runtime. You would have to implement this yourself in C++. There is a system called Datasmith Runtime which can load various mesh formats at Runtime but this is not part of Geometry Scripting.

Can I use Geometry Script to modify Static Meshes in my Level at Runtime?

No, this is not possible. Static Mesh Assets you created in the Editor and placed in a level are “cooked” when you create your game executable. It is not possible to update a cooked asset at Runtime, the mesh data has been converted to optimized GPU index and vertex buffers.

The function “Copy Mesh From Static Mesh” is not working at Runtime

Try checking the Output Log, you will likely see that there are warning messages about the “Allow CPU Access” flag on the Static Mesh Asset. You must enable this flag in the Editor to be able to access the StaticMesh index and vertex buffers on the CPU at Runtime. Note that this will increase memory usage for the Asset.

The Mesh I get when using “Copy Mesh From Static Mesh” at Runtime is different than the mesh I get in the Editor

In the Editor, by default CopyMeshFromStaticMesh will access the “Source” mesh, however at Runtime the Source mesh is not available. Even with the Allow CPU Access flag enabled, at Runtime only the “cooked” index and vertex buffers that will be passed to the GPU are available on the CPU. This representation of the mesh does not support “shared” or “split” UVs or normals, the mesh will be split along any UV and hard-normal seams. So what would be a closed solid cube in the Editor will become 6 disconnected rectangles in the index/vertex buffer representation. This is problematic for many mesh modeling operations. You can in many cases use the Weld Mesh Edges function to merge the mesh back together at the added seams, however this may introduce other problems, and very small triangles may have been fully discarded.

The functions “Apply Displace from Texture Map” and/or “Sample Texture2D at UV Positions” are working in the Editor but not at Runtime

Try checking the Output Log, you will likely see warning messages about Texture Compression. In their cooked representation, Texture2D Assets are generally compressed in formats that can only be efficiently decompressed on the GPU, and so are not readable in Geometry Script. The VectorDisplacementMap texture compression mode in the Texture2D Asset is effectively uncompressed RGBA8, so you must configure a Texture asset with this compression mode in the Editor for it to be readable at Runtime.

Rendering and UE Features

Does DynamicMeshComponent support Nanite, Lumen, or Mesh Distance Fields?

As of 5.1, no.

Does DynamicMeshComponent work with Runtime Virtual Texturing (RVT)?

As of 5.1, no. RVT requires usage of the Static Draw Path, and DynamicMeshComponent uses the Dynamic Draw Path

Does DynamicMeshComponent support Physics / Collision?

Yes. DynamicMeshComponent supports both Complex and Simple collision, similar to StaticMesh. The Collision settings and geometry are stored on the DynamicMeshComponent, not the DynamicMesh directly (unlike how they are stored on a StaticMesh Asset). So, to set collision geometry or change settings, you must call functions on the Component, not on the DynamicMesh.

DynamicMeshComponents don’t show up in Collision Debug Views!

This is currently not supported in UE 5.1

Does DynamicMeshComponent support LODs?

No.

Does DynamicMeshComponent support Instanced Rendering?

As of 5.1, no.

Lyra Sample Game

How does the Non-Destructive Level Design with GeometryScript-based mesh generator “Tool” objects work in Lyra?

I wrote extensive documentation for the Lyra Tool system here: https://docs.unrealengine.com/5.0/en-US/lyra-geometry-tools-in-unreal-engine/. The basic principle is that StaticMeshComponents are linked with a GeneratedDynamicMeshActor “Tool” mesh generator which still exists in the level (they are “stored” under the map). A helper Actor called the “Cold Storage” is used to maintain links between the Tool instance and it’s Components. Each Tool must be associated with a single StaticMesh Asset.

How can I migrate the Lyra Tool system to my own project?

This is somewhat complex, and the simplest route would be to migrate your content in a copy of the Lyra game. However several users have figured out how to migrate from Lyra to your own project. This YouTube tutorial by BuildGamesWithJohn is one that I believe will work, and other users have reported that this tutorial by JohnnyTriesVR will also work.

The Interactive Tools Framework in UE5

During the last few major versions of UE4, a stack of libraries was built up in the service of the new and expanding Modeling Editor Mode. This included a low-level mesh/geometry processing plugin (cleverly named GeometryProcessing), the InteractiveToolsFramework, and the MeshModelingToolset plugin. In UE5 these libraries have been significantly expanded, but also undergone some major reorganization, and and some portions have been taken out of Experimental status.

In previous Tutorials, I have covered using these libraries in-Editor to build custom Modeling Tools (https://www.gradientspace.com/tutorials/2020/1/2/libigl-in-unreal-engine), doing command-line Geometry Processing (https://www.gradientspace.com/tutorials/2020/9/21/command-line-geometry-processing-with-unreal-engine), doing Runtime Procedural Mesh Generation (https://www.gradientspace.com/tutorials/2020/10/23/runtime-mesh-generation-in-ue426 and https://www.gradientspace.com/tutorials/2020/11/11/procedural-mesh-blueprints-in-ue426), and most recently, using the Interactive Tools Framework (ITF) to build a small Runtime 3D Modeling App (https://www.gradientspace.com/tutorials/2021/01/19/the-interactive-tools-framework-in-ue426). With the changes in 5.0, all these posts and sample projects need to be updated (not a small effort!).

In this article I will describe the high-level changes to the ITF / GeometryProcessing / MeshModelingToolset stack. This will serve as a rough “porting guide” for UE4 usage of these libraries. I have also updated the Runtime Tools Framework Demo to work with UE5, the updated code project is available on Github (https://github.com/gradientspace/UE5RuntimeToolsFrameworkDemo), and I will discuss some details later in the post.

GeometryProcessing

Several major structural changes were made to the GeometryProcessing Plugin. The first and foremost is that portions of it were moved into the Engine core, to a module named GeometryCore. This was necessary to allow the core Engine and Editor to use the various Geometry algorithms, as they cannot easily have plugin dependencies. Specifically the contents of the GeometricObjects module of GeometryProcessing were moved, and that module no longer exists. So, to update your Build.cs files, generally you can just replace the “GeometricObjects” references with “GeometryCore”. Over time more GeometryProcessing functionality may migrate to GeometryCore as it becomes needed for core Engine features.

The core FDynamicMesh3 class and various associated types were also moved from the DynamicMesh module (although that module still exists and contains many processing algorithms). The paths to these files has changed, so for example where you could previously #include “DynamicMesh3.h”, you will now have to #include “DynamicMesh/DynamicMesh3.h”. A few other frequently-used utility headers like MeshNormals.h, MeshTangents.h, and MeshTransforms.h were also moved to this new DynamicMesh subfolder of GeometryCore.

Another major change is that nearly all code in GeometryCore and GeometryProcessing was moved to a namespace, UE::Geometry::. Moving code into this namespace resolved many naming conflicts with Engine types, and reduces the need to use highly verbose naming to avoid conflicts in the global namespace. This does, however, tend to mean any code written against GeometryProcessing will need some updates. Most code in the engine simply does a using namespace UE::Geometry; in any affected .cpp files, however this should never be done in a header. Generally the Engine uses explicit full names for UE::Geometry types in headers, eg in class definitions that are not also in the UE::Geometry namespace. In some cases you will also find class-scoped using declarations like using FDynamicMesh3 = UE::Geometry::FDynamicMesh3;

The GeometryProcessing plugin in UE4 was a largely self-contained set of libraries. The core GeometricObjects library even defined it’s own templated math types for Vectors/etc. This was because the core FVector type in UE4 used 32-bit float precision, and GeometryProcessing primarily uses doubles. In UE5, the rest of the Engine has caught up with GeometryProcessing, and the core FVector is now double-precision, a specialization of the UE::Math::TVector<T> template.

A major complication of this conversion was that the “short names” for the new explicit float and double core types were chosen to be FVector3f and FVector3d, exactly the global-scoped type names that had been used in GeometryProcessing for it’s templated Vector type. So, to resolve this conflict, and simplify usage of GeometryProcessing across the Engine, the GeometryProcessing FVector3<T> template was fully replaced by the new UE::Math::TVector<T>. Similar changes were made for TVector2 and a few other types. This may sound straightforward, but GeometryProcessing had used some vector-math naming and idioms common to external libaries like Eigen, that were in conflict with some of the “Unrealisms” of FVector. So, some former functions of GeometryProcessing’s FVector2/3/f/d were moved to standalone functions, to avoid duplication in the core Vector type. For example FVector3d.Normalized() no longer exists as a member function, and a free-function UE::Geometry::Normalized() must now be used. These changes required extensive (but very rote) refactoring of the entire GeometryProcessing library. As a result, most UE4 GeometryProcessing-based vector-math code is likely to not compile in UE5 without similar modifications.

Some other type conflicts were resolved by renaming the GeometryProcessing type, rather than by switching to the Engine types. In particular, the UE::Geometry variant of FTransform remains, and was renamed to FTransformSRT3f/d to resolve the name conflict and more clearly indicate it’s functionality (“SRT” indicates the Scale/Rotate/Translate transform order applied to points). In future there may be variants that could (for example) support composition of transforms with non-uniform scaling, which is not possible with the core Engine FTransform3f/d. In general, where UE::Geometry has “it’s own” version of a type, the goal is to provide a variant that is more compatible with standard math libraries and “textbook” equations, which in turns simplifies integration of those libraries by licensees, porting algorithms, etc. A prime example is the UE::Geometry::TMatrix3, which uses textbook post-multiplication ordering for matrix/matrix multiplies, vs the Engine TMatrix which uses a somewhat unusual pre-multiplication-of-transpose, that can trip up attempts to (eg) implement a formula one might find online or in a research paper.

Finally, GeometryCore and GeometryProcessing were taken out of Experimental status. What this means is that in future breaking changes will generally not be made without going through standard UE deprecation processes, ie APIs that need to be modified will be deprecated for an Engine release before being removed.

GeometryFramework

A central character in several of my previous tutorials was the USimpleDynamicMeshComponent class, which provided a renderable Component based on FDynamicMesh3. In UE4 this was primarily used by Modeling Mode, to support fast live previews of mesh editing, and could also be created and used at Runtime. In UE5, this Component has been become a fully-functional type, and was renamed to UDynamicMeshComponent. It was also moved from the ModelingComponents module of the MeshModelingToolset plugin, to a core Engine module named GeometryFramework, which now also includes an associated Actor type, ADynamicMeshActor, as well as UDynamicMesh, a UObject wrapper for a FDynamicMesh3.

UDynamicMeshComponent was significantly “cleaned up”, and some areas that were previously a bit ad-hoc, like support for Tangents, are now much cleaner. Support for both Simple and Complex collision was added, and a full UBodySetup API is included, as well as various helper functions. A key thing to note about Physics support, though, is that Async physics build is not supported, ie changes to collision geometry require a relatively slow game-thread recomputation. Async physics build has been added in the UE5 Main development stream and will land in 5.1.

FDynamicMesh3 is now serializable, and the UDynamicMesh wrapper can be added as a UProperty of any UObject. UDynamicMeshComponent now uses a UDynamicMesh to store it’s mesh, rather than directly storing a FDynamicMesh3. This means UDynamicMeshComponent is serializable, ie you can add an instance to any Actor, initialize/edit the UDynaimcMesh, and it will save/load as expected, and be included in the cooked game build.

Note, however, that UDynamicMesh is not currently an “asset type”, ie you cannot make one in the Content Browser like a UStaticMesh. Technically nothing prevents you from writing your own code to do that, as an Asset is simply a serialized UObject. However by default the UDynamicMeshComponent will create it’s own UDynamicMesh instance, and it will be serialized “with the Component”, which means it is stored “in the level”. I will cover this in depth in future Tutorials.

To avoid breaking code, the direct FDynamicMesh3 access functions of UDynamicMeshComponent still exist, such as FDynamicMesh3* GetMesh(). However, it is strongly recommended that the ProcessMesh() and EditMesh() functions be used instead. These give UDynamicMesh/Component some control over when the mesh update actually occurs, which (in future) will allow for safe access from multiple threads, ie mesh updates will not need to all be done on the game thread. These two functions also exist on UDynamicMesh, as well as other “mesh containers” like UPreviewMesh that are used heavily in MeshModelingToolset.

ADynamicMeshActor is a standard Actor type for a UDynamicMeshComponent, similar to AStaticMeshActor and UStaticMeshComponent. It is Blueprintable, and the new Geometry Script plugin can be used to do mesh generation and editing for UDynamicMeshActor/Component in Blueprints. I won’t discuss that further here, but I do have an extensive series of Youtube videos on the topic. Similarly, DynamicMeshActors can now be emitted by the mesh creation Tools in Modeling Mode, and similarly the mesh editing Tools generally all work on DynamicMeshComponents.

InteractiveToolsFramework

The Interactive Tools Framework (ITF) has become more deeply integrated into the UE Editor, while still remaining fully functional for Runtime use. Usage is no longer limited to Modeling and Pain modes, many UE Editor Modes now use the ITF to some extent. However some major refactoring has occurred to support this broader usage base. In particular some aspects of the ITF were quite specific to Modeling, and an attempt has been made to remove these aspects, or at least make them optional.

UToolTargets

Perhaps the most significant change is that the previous way that Modeling Tools interacted with “Mesh Objects” like a StaticMesh or Volume, via FPrimitiveComponentTarget, has been deprecated and replaced. FPrimitiveComponentTarget was a relatively simple wrapper around something that could provide a FMeshDescription, which was used to bootstrap the Modeling Mode, however it had major problems. In particular, it relied on a global registry, which meant that if an Engine module registered a FComponentTargetFactory, a plugin could not easily override that Factory (even at Runtime). Similarly, since the Engine does not support RTTI, it was quite cumbersome for a plugin to extend the core FPrimitiveComponentTarget API with additional functionality without making Engine changes, and then build Tools that used that functionality.

The replacement is the UToolTarget system, where a base UToolTarget class defines no functionality itself, and UInterfaces are used to add sets of API functions. The UObject system supports run-time checked type querying/casting, which allows the Tool system to then determine if a given UToolTarget supports a particular UInterface. For example the IPrimitiveComponentBackedTarget interface provides functions for accessing the Actor, Component, Transform, etc of a PrimitiveComponent, and the IMeshDescriptionProvider interface provides APIs for accessing a MeshDescription for a given ToolTarget.

To avoid the global-registry problem, UToolTargetFactory implementations for particular Component/Object types are registered with the UToolTargetManager, which lives in the UInteractiveToolsContext, adjacent to the ToolManager, GizmoManager, and so on. A given UToolTarget implementation like UStaticMeshComponentToolTarget will implement various of the APIs above, and an Editor Mode will register it’s Factory with the ToolTargetManager on setup (see UModelingToolsEditorMode::Enter() as an example).

To support “capability queries”, ie to ask the ToolTargetManager if it can build a ToolTarget for a given target Object (Actor, Component, Asset, etc) and set of required ToolTarget APIs, there is a FToolTargetTypeRequirements type. The common usage is that a ToolBuilder will have a static FToolTargetTypeRequirements enumerating the APIs it requires, which will be passed to the ToolTargetManager. An example such function is shown below for UBaseMeshProcessingTool/Builder.

const FToolTargetTypeRequirements& UBaseMeshProcessingToolBuilder::GetTargetRequirements() const
{
	static FToolTargetTypeRequirements TypeRequirements({
		UMaterialProvider::StaticClass(),
		UMeshDescriptionCommitter::StaticClass(),
		UMeshDescriptionProvider::StaticClass(),
		UPrimitiveComponentBackedTarget::StaticClass()
		});
	return TypeRequirements;
}

The UToolTarget system is highly flexible, as it does not explicitly define any base interfaces or require specific object types. A ToolTarget Interface can be defined for any UObject type, which then allows Tools to manipulate instances of that UObject - or even specific UObjects - via the published UInterfaces.

UContextObjectStore

In addition to UToolTargetManager, a very generic mechanism for passing objects down into Tools from higher levels has been added to the InteractiveToolsContext, the UContextObjectStore. This is, to be blunt, basically just a list of UObject pointers, that can be searched by class type. The basic usage is to add an object to the Store, eg ToolsContext->ContextObjectStore->AddContextObject(NewObject<SomeUType>()), and then later that UObject instance can be found by querying ToolsContex->ContextObjectStore->FindContext<SomeUType>(). Other Manager types like the ToolManager have helper functions to access the ContextObjectStore.

The purpose of the ContextObjectStore was to replace the proliferation of ToolsContext APIs that ITF implementors were required to provide. For example, the previous strategy to expose some UE Editor functionality would have been to abstract it in an interface like the IToolsContextQueriesAPI. However expanded usage of the ITF in the Editor means that more information needs to be passed from the Editor to Tools, and abstracting all those channels via APIs at the ITF level would be very complex. So, the ContextObjectStore was intended to be used to pass Editor-level API abstractions (or simply Editor-level objects and data structures directly) in a generic way, customizable for specific “Editor”/”Client” situations.

A mechanism like the ContextObjectStore can be easily abused, however. It is nothing more than a shared list of UObject pointers, effectively a global list from the PoV of Tools living inside a given ToolsContext. So, for example, any UObject instance can be added to the store, and the store will prevent that object from being garbage collected, as long as it exists. Similarly multiple objects of the same type can be added, and only the first will ever be found. Or by the same token, nothing prevents “someone else” from removing a context object you added.

If you go spelunking, you will find some places in the UE codebase where the ContextObjectStore has been used for purposes other than “Editor-level providing abstract/generic APIs to Tool-level”, and is instead used as a convenient way to pass data members around. I strongly encourage you to not treat those usages as a pattern that should be followed. Ask yourself, “would I consider passing this data by temporarily sticking it in a global void-pointer array”? If the answer is a clear no, then using the ContextObjectStore is probably not the right approach.

UModelingObjectsCreationAPI

The IToolsContextAssetAPI in the UE4 ITF is a prime example of the type API that is better done via the ContextObjectStore. That API was used by Tools to emit new Assets, which required some abstraction to permit Runtime usage of the ITF. However the ToolsContext was required to provide an IToolsContextAssetAPI implementation, even if it did not have the concept of Assets (ie, at Runtime!). And then because that API existed, many Modeling Tools emitted “Assets” even though they were actually just trying to emit “Meshes”, which limited how easily they could be adapted to different use cases.

To resolve this situation, IToolsContextAssetAPI has been removed from the ITF in UE5, and the core ITF has no concept of “emitting Assets”. Instead, a UModelingObjectsCreationAPI type has been defined in the ModelingComponents module of MeshModelingToolset. This type contains a function CreateMeshObject() which Tools can use to create new ‘Mesh Objects’, which could be a StaticMesh Asset, but also could be a Volume, DynamicMeshActor, or any other Mesh Type (eg as we will do in our Runtime demo below). UEditorModelingObjectsCreationAPI is the implementation used in Modeling Mode in the UE Editor.

The ContextObjectStore is used to provide an implementation of UModelingObjectsCreationAPI to the Modeling Tools. Primarily the Tools use a static utility function UE::Modeling::CreateMeshObject(), which finds the UModelingObjectsCreationAPI implementation in the ContextObjectStore, and uses it to create the Mesh Object. An extensive FCreateMeshObjectParams struct is used to provide mesh creation information, ie names, materials, the source MeshDescription or DynamicMesh, and so on. Similarly the function returns a FCreateMeshObjectResult that provides pointers to the new Actor, Component, and Asset, where applicable.

A similar set of functions and types is available for Texture objects, and more are likely to be added in the future. Note, however, that support for this API is completely optional - a Runtime ITF implementation would only need to provide a UModelingObjectsCreationAPI implementation if it was to use MeshModelingToolset Tools that emit new Mesh Objects.

UCombinedTransformGizmo

The UTransformGizmo developed for Modeling Mode in the UE Editor is designed to also work at Runtime, however this means it’s behavior in the UE Editor is not ideal (particularly for rendering), and it has a significantly different UX. To make way for a future Gizmo implementation, UTransformGizmo was renamed to UCombinedTransformGizmo. In addition, the concept of “default Gizmos” is in the process of being removed from the GizmoManager, and so usage of UCombinedTransformGizmo should now be done via a set of utility functions in /BaseGizmos/TransformGizmoUtil.h.

To create new 3D Gizmos from Modeling Tools and Runtime ITF code, a helper object can be automatically registered in the ContextObjectStore using the function UE::TransformGizmoUtil::RegisterTransformGizmoContextObject(), and similarly unregistered using DeregisterTransformGizmoContextObject(). Once registered, the utility functions UE::TransformGizmoUtil::Create3AxisTransformGizmo() and ::CreateCustomTransformGizmo() are available and should replace previous calls to UInteractiveGizmoManager::CreateTransformGizmo(). However Gizmos can be discarded the same way as before, using the various UInteractiveGizmoManager::DestroyGizmo() variants.

Finally, if you previously tried to use UTransformGizmo in your own projects, you will likely have run across the need to call GizmoRenderingUtil::SetGlobalFocusedSceneViewTrackingEnabled(). This was, to be blunt, a very gross hack needed to work around limitations of communicating between the game thread and render thread, because the sub-Components used in the Gizmo figure out some aspects of their rendering on the render thread. This caused no end of problems in the Editor, and so it was removed and replaced with a more structured system based on an object called the UGizmoViewContext. This object is created and added to the ContextStore (again…) by the TransformGizmoUtil registration function above. It is then necessary to update this GizmoViewContext with the active FSceneView every frame. This is generally straightforward and you can see how it is used in the sample project below, in the function URuntimeToolsFrameworkSubsystem::Tick(). But just note that UCombinedTransformGizmo instances will not function without this SceneView being set correctly.

UInteractiveToolsContext Customization

The core ITF classes - UInputRouter, UInteractiveToolManager, UInteractiveGizmoManager, UToolTargetManager, and UContextObjectStore - are fully functional on their own, however for many users of the ITF it may be desirable to customize or extend the behavior of the base classes. This was previously somewhat difficult unless you also subclassed UInteractiveToolsContext and replaced the Initialize() function, which from a maintenance perspective is not ideal, as the base implementation may be extended in the future (as it was in UE5 to add the ToolTargetManager and ContextObjectStore). To simplify customization of these base Managers, the default UInteractiveToolsContext now allows you to provide custom functions to create and destroy each of the sub-objects.

This capability is used in the Editor, to support a “hierarchy” of InteractiveToolsContexts. This is useful information if you are building in-Editor Tooling using the ITF - in addition to each Editor Mode (UEdMode) having a local InteractiveToolsContext (ITC), there is also a ToolsContext that lives at the “ModeManager” level. This ITC is considered a “parent” ITC, and (for example) the InputRouter is shared between the Parent and any active Mode ITCs, to enforce “one capture at a time” behavior. You may find having a hierarchy of ToolsContexts helpful if you are building a complex at-Runtime DCC Tool. If you want to browse the Editor code for this, see the base class UEditorInteractiveToolsContext and subclasses UModeManagerInteractiveToolsContext and UEdModeInteractiveToolsContext.

UAssetEditors now also support UEdModes, and hence have a UInteractiveToolsContext in each Mode by default. This is not heavily used in existing Asset Editors, however the new UV Editor (a companion to Modeling Mode) is an example of an Asset Editor built primarily using the ITF. A variant of Modeling Mode has also been integrated into the Static Mesh Editor, although this is not enabled by default, and only exposes a few Tools there. The plugin is called Static Mesh Editor Modeling Mode, and can be found in the source tree in \Plugins\Experimental\StaticMeshEditorModeling\. This plugin is fully self-contained, ie no Engine changes are needed for a plugin to “add itself” to the StaticMeshEditor.

MeshModelingToolset / Exp

The MeshModelingToolset plugin has been moved out of Experimental status, however portions of the plugin and modules that needed to remain Experimental were then moved to a “MeshModelingToolsetExp” plugin. The only real effect of this in terms of porting projects is that your .uplugin and .build.cs files may need to be updated to add “MeshModelingToolsExp” and/or “MeshModelingToolsEditorOnlyExp”.

Runtime Tools Framework Sample Project

A port of the UE4 Sample Project to UE5 is available on github here: https://github.com/gradientspace/UE5RuntimeToolsFrameworkDemo. I made this project by forking the UE4 project, and then submitted the port in a single commit. So, if you are interested in what specifically had to be updated, or you need to perform a similar upgrade on your own project based on my sample, you can browse the diff here. I will give a high-level overview of the changes below

RuntimeGeometryUtils Plugin

This plugin was used in several of my other sample projects, it’s not really critical to this sample, but it provides the OBJ import and the ADynamicSDMCActor. Most of the changes are simply updating paths, dealing with the new UE::Geometry namespace, and some minor API and function changes. The URuntimeDynamicMeshComponent class was removed as it is no longer needed - it just added collision support to USimpleDynamicMeshComponent, but the replacement UDynamicMeshComponent in UE5 now includes full simple and complex collision support. To minimize changes involved in the port I left UGeneratedMesh intact, however the new engine UDynamicMesh class is a superior replacement, I hope to do that change in the future (and similarly for ADynamicSDMCActor, replacing with the Engine’s ADynamicMeshActor).

RuntimeToolsSystem Module

The RuntimeToolsSystem Module is the main code of the sample, and implements the “Tools Framework Back-End” for Runtime. This is where most of the changes have taken place.

As discussed above, the FPrimitiveComponentTarget system was removed in favor of the new UToolTarget system. So, URuntimeDynamicMeshComponentToolTarget has been deleted, and a new URuntimeDynamicMeshComponentToolTarget and URuntimeDynamicMeshComponentToolTargetFactory added in it’s place. This new ToolTarget factory is registered in URuntimeToolsFrameworkSubsystem::InitializeToolsContext().

To support creation of new meshes by the various Tools, a new URuntimeModelingObjectsCreationAPI implementation of UModelingObjectsCreationAPI was added. The ::CreateMeshObject() function spawns a new URuntimeMeshSceneObject (which is a wrapper for a mesh Actor/Component) via the URuntimeMeshSceneSubsystem. An instance of this API implementation is similarly registered in URuntimeToolsFrameworkSubsystem::InitializeToolsContext(). As it was no longer needed, the FRuntimeToolsContextAssetImpl implementation of IToolsContextAssetAPI was also removed (and that API no longer exists).

The above changes allow some of the Modeling Tool subclasses in the /Tools/ subfolder to be simplified. In particular, several Tools had to override base-class functions to handle creating new objects, because the previous AssetAPI-based versions could not be hacked to function correctly. With the new UModelingObjectsCreationAPI, the Tool-creates-new-Mesh-object flow is much cleaner and no longer required any customization at the Tool level.

Finally several small changes were needed to update support for the 3D Transform (TRS) Gizmo. First, The function UE::TransformGizmoUtil::RegisterTransformGizmoContextObject() must be called to register an instance of the UCombinedTransformGizmoContextObject in the ContextObjectStore, this is done in URuntimeToolsFrameworkSubsystem::InitializeToolsContext(). This object registers the various sub-gizmos with the GizmoManager, and provides a wrapper that can spawn instances of the new UCombinedTransformGizmo. In future this will not be directly possible via the GizmoManager (it still is in 5.0, for legacy reasons, but this is due to change). So, the next step is to update USceneObjectTransformInteraction to call UE::TransformGizmoUtil::CreateCustomTransformGizmo() instead of talking to the GizmoManager directly.

Finally, there had previously been calls in the AToolsContextActor to call GizmoRenderingUtil::SetGlobalFocusedSceneViewTrackingEnabled(). This was, frankly, a gross hack, that set global pointers which allowed the Gizmo to communicate information based on the FSceneView between the Game and Render threads. In 5.0 this is no longer necessary. Instead, in URuntimeToolsFrameworkSubsystem::Tick(), an instance of UGizmoViewContext is fetched from the ContextObjectStore, and passed the current FSceneView. This is all that is necessary to provide the Gizmo with correct camera information. The UGizmoViewContext is automatically created and configured by the GizmoRenderingUtil registration function that was called above.

And that’s it! Those are the major changes that were necessary.

If you run into problems, or have questions, please don’t hesitate to find me on twitter ( https://twitter.com/rms80 ) or on the Epic Dev Community ( https://forums.unrealengine.com/u/rmseg ).

Modeling Mode Extension Plugins in UE5

In Unreal Engine 5.0, Modeling Mode includes a large set of Tools, built using the Interactive Tools Framework, which allow users to create and edit meshes in the Level Viewport. However, something else that came with UE5.0 is the ability for third-party plugins to add additional Tools into Modeling Mode. In this tutorial I will explain how that works, and provide sample code that adds a small set of custom Tools.

I will not go deeply into the mechanics of implementing new Interactive Tools in this article. I have discussed this quite a bit in some previous posts, such as The Interactive Tools Framework and Interactive Mesh Processing with libigl. At time of writing, those Tutorials have not been updated for UE5, and some changes to the Interactive Tools Framework (ITF) APIs may have broken that older Tool code (updates to those posts are in progress and I will update this article when they are done). But the high-level concepts/etc are still applicable, and I have included a few basic UE5.0-style Tools with this article’s sample code.

The Tools will appear in their own section of the Modeling Mode tool palette, as shown in the image to the right - I called the extension “Extension Demo”, and there are 4 Tools - Noise, Cut, ClickBP, and MeshEdBP. Note that I set the color of this section using the Modeling Mode palette customization features, which I demonstrated in this YouTube Video. The Palette customization is completely separate from the Extension mechanism, but is fully functional with Extensions (so, for example, I could add an Extension Tool to my Favorites section).

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games. However, gradientspace.com is his personal website and this article represents his personal thoughts and opinions. This document and sample code are not supported by Epic Games!)

IModularFeature and the IModelingModeToolExtension API

Modular Features are a mechanism for core Unreal Engine and Editor code to support features and capabilities defined in plugins. Essentially, the way it works is that UE publishes standard interfaces, and then plugins can implement that interface and register themselves as a provider of an implementation. Various standard Editor/Engine features are implemented this way, but it also allows for third-party developers to provide their own implementation(s).

The core of the system is the IModularFeature interface, which doesn’t actually contain any functions, it’s just the magic base-class that makes the system work. If you search the codebase for “public IModularFeature” you will find many subclasses of this base class, all of these are different Modular Feature APIs that the engine supports in some way (I found 96 in UE5.0). In our case, we will be using IModelingModeToolExtension, which is defined in Engine\Plugins\Editor\ModelingToolsEditorMode\Source\ModelingToolsEditorMode\Public\ModelingModeToolExtensions.h. This is an API that Modeling Editor Mode uses to interact with the available Tool Extensions. Essentially, Modeling Mode will ask each registered extension “What Tools do you have for me?” and then it will add sections and buttons to the Modeling Mode Tool Palette to expose those Tools to the user. It is really that simple.

The IModelingModeToolExtension API has 3 functions, listed below (minus some boilerplate)

class IModelingModeToolExtension
{
  virtual FText GetExtensionName();
  virtual FText GetToolSectionName();
  virtual void GetExtensionTools(const FExtensionToolQueryInfo& QueryInfo, TArray<FExtensionToolDescription>& ToolsOut)
};

GetExtensionName() returns an identifier string that needs to be unique for your Extension. GetToolSectionName() returns the string that will be used in the Tool Palette. And GetExtensionTools() returns a list of FExtensionToolDescription objects, one per Tool, that Modeling Mode will use to create the Tool Palette button and launch the Tool on-click. This struct is shown below, again basically we have an identifier name, Command info for the Button (which includes the Icon), and then the ToolBuilder that Modeling Mode will use to create an instance of the Tool.

struct FExtensionToolDescription
{
	FText ToolName;                         // long name of the Tool
	TSharedPtr<FUICommandInfo> ToolCommand; // Command that is launched by the Palette
	UInteractiveToolBuilder* ToolBuilder;   // Tool Builder that will be called to create the Tool
};

The FExtensionToolQueryInfo struct passed to GetExtensionTools() by the Mode is for optional/advanced usage, we will skip it for now, and I’ll cover it below in the Extra Bits section.

So, basically, the way you use IModelingModeToolExtension is as follows:

1. Write some UInteractiveTool implementations, these are your Tools

2. Create a new Plugin, and subclass/implement IModelingModeToolExtension. Normally this is done in the same class as the IModuleInterface implementation, ie the class that contains the StartupModule()/ShutdownModule() functions (Note that your Tools do not have to be in this plugin/module, but they can be)

3. In the GetExtensionTools() function, return a list of your available Tools with a ToolBuilder for each

4. In the StartupModule() function, call IModularFeatures::Get().RegisterModularFeature(IModelingModeToolExtension::GetModularFeatureName(), this); (and similarly UnregisterModularFeature in ShutdownModule)

Step 4 is the critical one, basically this is how your Plugin/Module tells the Modular Feature system “Hey I implement this named Interface!”, where the name is provided by IModelingModeToolExtension::GetModularFeatureName(). Modeling Mode will (later) ask the Modular Feature system “Hey does anyone implement this named interface?”, and the Modular Feature system will say “Yes! This thing does!” and provide your implementation.

From the Point of View of the Extension Writer, this is all there is to it. There is a bunch of boilerplate in setting up the TCommands and Style objects for your plugin, which you can copy-paste from my sample, but the actual Modeling Mode Extension part only takes these few steps listed above.

The UE5ToolPluginDemo Sample Project

You can grab the UE5ModelingModeExtensionDemo project from the Gradientspace Github at https://github.com/gradientspace/UE5ModelingModeExtensionDemo. I have included the entire project, however this is just a generated standard UE5 Blank project template. All the relevant code for the sample is in \Plugins\SampleModelingModeExtension, which you can easily copy-paste to any other Project, as it has no dependencies on, or references to, the base Project.

There are 3 boilerplate/setup classes in the SampleModelingModeExtension plugin, lets briefly go through them:

FSampleModelingModeExtensionModule

This class is the main class for the Module, which implements IModuleInterface (ie StartupModule() / ShutdownModule() ) and our IModelingModeToolExtension Modular Feature API, discussed above. The cpp contains the bare minimum lines to register the Style, Commands, and Modular Feature, and provide the list of Tool description structs.

FSampleModelingModeExtensionStyle

The Style class is used to provide icons for the Tool Palette. If you had (for example) registered details customizations for property sets of the Tools, you might put additional things in this Style, but otherwise, it’s 100% copy-pastable boilerplate except the lines that look like this:

StyleSet->Set("SampleModelingModeExtensionCommands.BeginMeshNoiseTool", new IMAGE_BRUSH_SVG("Icons/NoiseTool", DefaultIconSize));

Note that the strings here are important. The SampleModelingModeExtensionCommands string is not the class name, but rather the string passed to the TCommands constructor in the FSampleModelingModeExtensionCommands class. I just tend to use the same string everywhere. The BeginMeshNoiseTool string is the name of the FUICommandInfo member variable of the FSampleModelingModeExtensionCommands, passed to the UI_COMMAND macro, and not (eg) the name of the Tool Icon or identifier string.

FSampleModelingModeExtensionCommands

This class is a subclass of TCommands, which uses the Curiously Recurring Template Pattern (CRTP - Wikipedia). Basically we just use this to provide UI Command objects that can be assigned to Tool Palette buttons. The UI Command system will provide the icon (via the Style), and the FExtensionToolDescription struct will let Modeling Mode link up the Command to the ToolBuilder you specify. So, again, this is really just lines of boilerplate that look like the following

UI_COMMAND(BeginMeshNoiseTool, "Noise", "Add Noise to selected Mesh", EUserInterfaceActionType::ToggleButton, FInputChord());

Where you will have one line for each Tool your plugin provides.

The Sample Tools

I have included 4 basic Tools in the sample project. UMeshNoiseTool is a basic tessellate-and-displace Tool, and UMeshPlaneCutTool shows how to create a 3D gizmo inside a Tool, and then use it to do a plane cut of the active mesh. In both cases the Tool subclasses the UBaseMeshProcessingTool base tool. This base tool provides very useful functionality for editing single meshes - in particular, it automatically computes the mesh operation asynchronously in a background thread, with support for cancelling. This is done via a FDynamicMeshOperator, you will find the simple Noise and PlaneCut operators in the .cpp files.

The Noise and PlaneCut tools are basic versions of the Displace and PlaneCut Tools in Modeling Mode. Many Tools in Modeling Mode are also derived from UBaseMeshProcessingTool (although for example the Modeling Mode Plane Cut Tool support operating on multiple objects, which adds a lot of complexity). However the other two Tools in this sample are unique in that they use a Blueprint to define their behavior (!)

UActorClickedBPTool

View fullsize

Users of modeling tools each have their own unique workflows, and this often results in feature requests for Tools that are extremely specific to a particular task or workflow. However, adding a new Tool tends to increase the cognitive load for all users, and at some point, a Tool is just “too niche” to add to the UI by default. In UE5.0, I added Geometry Script to allow end-users to create their own Tools in UE Blueprints. If you aren’t familiar with Geometry Script, I suggest you check out this playlist of short videos I have posted on YouTube. Using Geometry Script and Editor Utility Widgets, it is possible to make something that is similar to a Modeling Mode Tool, like I did in this video where I made a “convex hull wrapper” mesh generation Tool. However, this approach is a bit clunky compared to a Tool integrated into Modeling Mode.

So, UActorClickedBPTool is a Modeling Mode Tool that doesn’t have any built in behavior, and instead just executes an arbitrary function - defined in a Blueprint - on whatever Actor is clicked while using the Tool. You provide the BP function by subclassing the UActorClickedBPToolOperation object type, which has a function OnApplyActionToActor that can be overridden in the BP. When configured in the Tool, this function will be called on Actor click.

As a simple example, I implemented a BP Operation that flips the Normals of clicked StaticMeshActors. You will find the BP_FlipNormals blueprint operation in the /ActorClickBP Content folder. The entire Blueprint is shown below (click to enlarge the image). The gif above-right is a brief demo of using the Tool, assigning the FlipNormals BP, and then clicking on two meshes in the level a few times.

View fullsize

UMeshProcessingBPTool

After my success with the ActorClickedBPTool, I decided to try to make a variant of UBaseMeshProcessingTool where the mesh processing operation could be implemented in BP using Geometry Script. This is in theory no more complex than UActorClickedBPTool, however to avoid writing a lot of boilerplate code, I decided to directly subclass UBaseMeshProcessingTool, and just wrap the BP execution in a FDynamicMeshOperator like in the Noise and Plane Cut Tools. This basically works, and UMeshProcessingBPTool has the same structure as the ActorClickedBPTool, but in this case UMeshProcessingBPToolOperation is the base UObject class for the mesh processing operation, and BP subclasses implement the OnRecomputeMesh function which takes a UDynamicMesh as input/output.

I have included two MeshProcessingBPToolOperation examples in the /MeshEditBP content subfolder. BP_Noise is shown in the video below, it implements a simple PN-Tessellation and Perlin-Noise displacement operation. This is basically the exact same Geometry Script setup as I have demonstrated in other videos, just running in the context of an Interactive Tool. BP_Boxes is a simple blueprint that appends random cubes to the input mesh, not particularly useful, I just wanted a second example.

Now, there is a subtle complication with this setup. You may recall that earlier I mentioned that UBaseMeshProcessingTool automatically evaluates it’s FDynamicMeshOperators in background threads. However, it is generally not safe to access UObjects in background threads, and so (in general) Blueprints also cannot be executed asynchronously. A conundrum! To work around this, in the MeshProcessingBPTool I have added a bit of a hack, where by default the Operator will (via a helper class) force the BP execution to occur on the Game thread (generally making the background thread computation useless)

However, I have found that in fact it is not catastrophic to evaluate the Mesh Processing BP operation from the background thread, as long as it does not touch any Actors/Assets/Components/Subsystems except the input UDynamicMesh. This is, as far as I am aware, 100% off-book, unsupported usage of Unreal Engine, and may not continue to work in the future. But it does seem to work now, in 5.0, and allows the Mesh Processing BP to be executed asynchronously. To enable this, the UMeshProcessingBPToolOperation BP base class has a second function, GetEnableBackgroundExecution, that you can override in the BP to return true (instead of default false).

UMeshProcessingBPTool Parameters

One caveat with the MeshProcessingBPTool (and the UActorClickedBPTool) is that there is currently no way for the Blueprint to expose parameters in the Modeling Mode Tool Settings panel without making some C++ modifications. The way I have done it in the sample is to make a small UStruct, FMeshProcessingBPToolParameters, which contains 2 float parameters and 2 integer parameters. An instance of this struct is included in the UMeshProcessingBPToolProperties, which results in it being included in the Tool Settings details panel. A copy of this struct is passed to the UMeshProcessingBPToolOperation::OnRecomputeMesh() function, allowing the UI to be used to control settings in the mesh processing BP. However, of course if you need more parameters or need to do any customization/etc, you will have to edit the C++ struct. This is not difficult, but it’s also not convenient.

The challenge is that only UInteractiveToolPropertySet subclasses can be passed by the Tool to the UI level. This type is currently not extendable in Blueprint, although this could be added in a C++ subclass. One way to possibly approach this problem would be to have the BP Operation subclass provide a set of such Blueprint-defined-Property-Sets. However the Tool would have to query the BP and manage the resulting Property Set instances, and…something…would have to copy values back-and-forth. It seems a bit tricky but perhaps a motivated reader will figure out a solution!

Adding More Tools

To add a new Tool, there are just a few steps

1. Create your Tool implementation (ie MyNewTool.h and .cpp)

2. Add a new FUICommandInfo to FSampleModelingModeExtensionCommands, in the header and cpp. This will be used to launch your Tool. The UI_COMMAND macro defines the icon label and tooltip

3. Add a new icon in the StyleSet in FSampleModelingModeExtensionStyle::Initialize(), as described above, with the label matching the Command from step 2

4. Add a FExtensionToolDescription struct for your Tool in FSampleModelingModeExtensionModule::GetExtensionTools(), using the right Command and ToolBuilder for your new Tool. You will likely also have to include your MyNewTool.h header (to access the ToolBuilder)

That’s it! When you build and run, your new Tool should be included in the Modeling Mode tool palette.

Miscellany

One last thing to mention is the FExtensionToolQueryInfo struct passed to the IModelingModeToolExtension::GetExtensionTools() function. This data structure is used to provide Modeling Mode’s UInteractiveToolsContext to the Extension, as some Extensions may need access to the Context. In addition, when Extensions are initially being queried for the Tool Palette setup, the Tool Builders are not actually required yet, and creating them can be skipped (in some cases this might be necessary or at least more performant). The FExtensionToolQueryInfo.bIsInfoQueryOnly flag will tell your Extension about this info. But this is optional/advanced usage and probably not something to worry about!

I also just wanted to mention that this Modeling Mode Extension system is not just for third parties, it is also used to add optional toolsets in the UE codebase. In particular the HairModelingToolset plugin adds a small set of tools for working with Groom Assets. These Tools were formerly included directly in Modeling Mode, however by moving them to a separate, optional plugin, they can be left disabled by default, and only enabled for users who need Groom Asset Editing. This is precisely the kind of niche toolset that Modeling Mode Extensions are intended to support.

Conclusions

Modeling Mode Extensions allow third parties to greatly increase the power of Modeling Mode in UE5. Even if you don’t want to write your own Tools from scratch, most existing Modeling Tools can be subclassed and customized to make them work better for specific use cases, and those custom versions exposed via an Extension. I am interested in hearing from readers about what kinds of “Base Tools” they might find useful to build on (particular in the case of Tools that can be customized with Blueprints). For example, I think a “Base BP Tool” that supports a generic brush-style interaction, calling a BP for each brush stamp, could be very interesting. Maybe something to tackle in a future post!

Similarly, if you find yourself trying to write a Tool Extension and hitting a wall, please don’t hesitate to post in the comments or get in touch on twitter @rms80.

The Interactive Tools Framework in UE4.26 (at Runtime!)

In this article, I am going to cover a lot of ground. I apologize in advance for the length. However, the topic of this article is essentially “How to Build 3D Tools using Unreal Engine”, which is a big one. By the end of this article, I will have introduced the Interactive Tools Framework, a system in Unreal Engine 4.26 that makes it relatively straightforward to build many types of interactive 3D Tools. I’m going to focus on usage of this Framework “at Runtime”, ie in a built Game. However, this exact same Framework is what we use to build the 3D Modeling Tools suite in the Unreal Editor. And, many of those Tools, are directly usable at Runtime! Sculpting in your Game! It’s pretty cool.

There is a short video of the ToolsFramworkDemo app to the right, and are a few screenshots below - this is a built executable, not running in the UE Editor (although that works, too). The demo allows you to create a set of meshes, which can be selected by clicking (multiselect supported with shift-click/ctrl-click), and a 3D transform gizmo is shown for the active selection. A small set of UI buttons on the left are used to do various things. The Add Bunny button will import and append a bunny mesh, and Undo and Redo do what you might expect. The World button toggles the Gizmo between World and Local coordinate systems.

The rest of the buttons launch various Modeling Tools, which are the exact same tool implementations as are used in Modeling Mode in the UE 4.26 Editor. PolyExtrude is the Draw Polygon Tool, in which you draw a closed polygon on a 3D workplane (which can be repositioned by ctrl-clicking) and then interactively set the extrusion height. PolyRevolve allows you to draw an open or closed path on a 3D workplane - double-click or close the path to end - and then edit the resulting surface of revolution. Edit Polygons is the PolyEdit tool from the Editor, here you can select faces/edges/vertices and move them with a 3D gizmo (note that the various PolyEdit sub-operations, like Extrude and Inset, are not exposed in the UI, but would work if they were). Plane Cut cuts the mesh with a workplane and Boolean does a mesh boolean (requires two selected objects). Remesh retriangulates the mesh (unfortunately I couldn’t easily display the mesh wireframe). Vertex Sculpt allows you to do basic 3D sculpting of vertex positions, and DynaSculpt does adaptive-topology sculpting, this is what I’ve shown being applied to the Bunny in the screenshot. Finally the Accept and Cancel buttons either Apply or Discard the current Tool result (which is just a preview) - I’ll explain this further below.

19/06/22 - This article is now somewhat out-of-date, and the sample project is broken in UE5. I have published a working port of the sample project to UE5 here: https://github.com/gradientspace/UE5RuntimeToolsFrameworkDemo, and an article about what has changed here: https://www.gradientspace.com/tutorials/2022/6/1/the-interactive-tools-framework-in-ue5 . If you are just interested in what changed in the code, the port was done in a single commit so you can browse the diffs.

All This geometry was created in the demo. Window is selected and being rotated with gizmo.

oh no bunny is growing some new parts

This is not a fully functional 3D Modeling tool, it’s just a basic demo. For one, there is no saving or export of any kind (wouldn’t be hard to add a quick OBJ export, though!). Support for assigning Materials is non-existent, the Materials you see are hardcoded or automatically used by the Tools (eg flat shading in the Dynamic Mesh Sculpting). Again, a motivated C++ developer could add things like that relatively easily. The 2D user interface is an extremely basic UMG user interface. I’m assuming that’s throw-away, and you would build your own UI. Then again, if you wanted to do a very simple domain-specific modeling tool, like say a 3D sculpting tool for cleaning up medical scans, you might be able to get away with this UI after a bit of spit-and-polish.

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games. However, gradientspace.com is his personal website and this article represents his personal thoughts and opinions. About triangles.)

Getting and Running The Sample Project

Before we begin, this tutorial is for UE 4.26, which you can install from the Epic Games Launcher. The project for this tutorial is on Github in the gradientspace UnrealRuntimeToolsFrameworkDemo repository (MIT License). Currently this project will only work on Windows as it depends on the MeshModelingToolset engine plugin, which is currently Windows-only. Getting that plugin to work on OSX/Linux would mainly be a matter of selective deleting, but it would require an Engine source build, and that’s beyond the scope of this tutorial.

Once you are in the top-level folder, right-click on ToolsFrameworkDemo.uproject in Windows Explorer and select Generate Visual Studio project files from the context menu. This will generate ToolsFrameworkDemo.sln, which you can use to open Visual Studio. You can also open the .uproject directly in the Editor (it will ask to compile), but you may want to refer to the C++ code to really understand what is going on in this project.

Build the solution and start (press F5) and the Editor should open into the sample map. You can test the project in PIE using the large Play button in the main toolbar, or click the Launch button to build a cooked executable. This will take a few minutes, after which the built game will pop up in a separate window. You can hit escape to exit full-screen, if it starts up that way (I think it’s the default). In full-screen, you’ll have to press Alt+F4 to exit as there is no menu/UI.

Overview

This article is so long it needs a table of contents. Here is what I am going to cover:

First, I am going to explain some background on the Interactive Tools Framework (ITF) as a concept. Where it came from, and what problem it is trying to solve. Feel free to skip this author-on-his-soapbox section, as the rest of the article does not depend on it in any way.

Next I will explain the major pieces of the UE4 Interactive Tools Framework. We will begin with Tools, ToolBuilders, and the ToolManager, and talk about Tool Life Cycles, the Accept/Cancel Model, and Base Tools. Input handling will be covered in The Input Behavior System, Tool settings stored via Tool Property Sets, and Tool Actions.

Next I will explain the Gizmos system, for implementing in-viewport 3D widgets, focusing on the Standard UTransformGizmo which is shown in the clips/images above.

At the highest level of the ITF, we have the Tools Context and ToolContext APIs, I’ll go into some detail on the 4 different APIs that a client of the ITF needs to implement - IToolsContextQueriesAPI, IToolsContextTransactionsAPI, IToolsContextRenderAPI, and IToolsContextAssetAPI. Then we’ll cover a few details specific to mesh editing Tools, in particular Actor/Component Selections, FPrimitiveComponentTargets, and FComponentTargetFactory.

Everything up to this point will be about the ITF modules that ship with UE4.26. To use the ITF at Runtime, we will create our own Runtime Tools Framework Back-End, which includes a rudimentary 3D scene of selectable mesh “scene objects”, a pretty standard 3D-app transform gizmo system, and implementations of the ToolsContext APIs I mentioned above that are compatible with this runtime scene system. This section is basically explaining the extra bits we have to add to the ITF to use it at Runtime, so you’ll need to read the previous sections to really understand it.

Next I’ll cover some material specific to the demo, including ToolsFrameworkDemo Project Setup that was necessary to get the demo to work, RuntimeGeometryUtils Updates, in particular collision support for USimpleDynamicMeshComponent, and then some notes on Using Modeling Mode Tools at Runtime, because this generally requires a bit of glue code to make the existing mesh editing Tools be functional in a game context.

And that’s it! Let’s begin…

Interactive Tools Framework - The Why

I don’t love the idea of starting an article about something by justifying it’s existence. But, I think I need to. I have spent many years - basically my entire career - building 3D Creation/Editing Tools. My first system was ShapeShop (which hasn’t been updated since 2008 but still works - a testament to Windows backwards compatibility!). I also built Meshmixer, which became an Autodesk product downloaded millions of times, and is widely used to this day. I am continually amazed to discover, via twitter search, what people are doing with Meshmixer (a lot of digital dentistry!!). I’ve also built other fully-functional systems that never saw the light of day, like this 3D Perspective Sketching interface we called Hand Drawn Worlds I built at Autodesk Research. After that, I helped to build some medical 3D design tools like the Archform dental aligner planning app and the NiaFit lower-leg prosthetic socket design tool (in VR!). Oh and Cotangent, which sadly I abandoned before it had any hope of catching on.

Self-congratulation aside, what I have learned over the last 15-odd years of making these 3D tools is that it is incredibly easy to make a giant mess. I started working on what became Meshmixer because Shapeshop had reached a point where it was just impossible to add anything to it. However, there were parts of Shapeshop that formed a very early “Tool Framework”, which I extracted and used as the basis for various other projects, and even bits of Meshmixer (which also ultimately became very brittle!). The code is still on my website. When I left Autodesk, I returned to this problem, of How To Build Tools, and created the frame3Sharp library which made it (relatively) easy to build at-Runtime 3D tools in a C# Game Engine. This framework grew around the Archform, NiaFit, and Cotangent apps mentioned above, and powers them to this day. But, then I joined Epic, and started over in C++!

So, that’s the origin story of the UE4 Interactive Tools Framework. Using this Framework, a small team (6-or-fewer people, depending on the month) has built Modeling Mode in UE4, which has over 50 “Tools”. Some are quite simple, like a Tool to Duplicate a thing with options, and some are extremely complex, like an entire 3D Sculpting Tool. But the critical point is, the Tools code is relatively clean and largely independent - nearly all of the Tools are a single self-contained cpp/h pair. Not independent by cutting-and-pasting, but independent in that, as much as possible, we have moved “standard” Tool functionality that would otherwise have to be duplicated, into the Framework.

Lets Talk About Frameworks

One challenge I have in explaining the Interactive Tools Framework is that I don’t have a point of reference to compare it to. Most 3D Content Creation tools have some level of “Tool Framework” in their codebase, but unless you have tried to add a feature to Blender, you probably have never interacted with these things. So, I can’t try to explain by analogy. And those tools don’t really try very hard to provide their analogous proto-frameworks as capital-F Frameworks. So it’s hard to get a handle on. (PS: If you think you know of a similar Framework, please get in touch and tell me!)

Frameworks are very common, though, in other kinds of Application Development. For example, if you want to build a Web App, or Mobile App, you are almost certainly going to be using a well-defined Framework like Angular or React or whatever is popular this month (there are literally hundreds). These Frameworks tend to mix low-level aspects like ‘Widgets’ with higher-level concepts like Views. I’m focusing on the Views here, because the vast majority of these Frameworks are based around the notion of Views. Generally the premise is that you have Data, and you want to put that data in Views, with some amount of UI that allows the user to explore and manipulate that Data. There’s even a standard term for it, “Model-View-Controller” architecture. The XCode Interface Builder is the best example I know of this, where you literally are storyboarding the Views that the user will see, and defining the App Behavior via transitions between these Views. Every phone app I use on a regular basis works this way.

Stepping up a level in complexity, we have Applications like, say, Microsoft Word or Keynote, which are quite different from a View-based Application. In these apps the user spends the majority of their time in a single View, and is directly manipulating Content rather than abstractly interacting with Data. But the majority of the manipulation is in the form of Commands, like deleting text, or editing Properties. For example in Word when I’m not typing my letters, I’m usually either moving my mouse to a command button so I can click on it - a discrete action - or opening dialog boxes and changing properties. What I don’t do is spend a lot of time using continuous mouse input (drag-and-drop and selection are notable exceptions).

Now consider a Content Creation Application like Photoshop or Blender. Again, as a user you spend the majority of your time in a standardized View, and you are directly manipulating Content rather than Data. There are still vast numbers of Commands and Dialogs with Properties. But many users of these apps - particularly in Creative contexts - also spend a huge amount of time very carefully moving the mouse while they hold down one of the buttons. Further, while they are doing this, the Application is usually in a particular Mode where the mouse-movement (often combined with modifier hotkeys) is being captured and interpreted in a Mode-specific way. The Mode allows the Application to disambiguate between the vast number ways that that the mouse-movement-with-button-held-down action could be interpreted, essentially to direct the captured mouse input to the right place. This is fundamentally different than a Command, which is generally Modeless, as well as Stateless in terms of in the Input Device.

In addition to Modes, a hallmark of Content Creation Applications are what I will refer to as Gizmos, which are additional transient interactive visual elements that are not part of the Content, but provide a (semi-Modeless) way to manipulate the Content. For example, small boxes or chevrons at the corners of a rectangle that can be click-dragged to resize the rectangle would be a standard example of a Gizmo. These are often called Widgets, but I think it’s confusing to use this term because of the overlap with button-and-menu Widgets, so I’ll use Gizmos.

So, now I can start to hint at what the Interactive Tool Framework is for. At the most basic level, it provides a systematic way to implement Modal States that Capture and Respond to User Input, which I’m going to call Interactive Tools or Tools for brevity, as well as for implementing Gizmos (which I will posit are essentially spatially-localized context-sensitive Modes, but we can save that discussion for Twitter).

Why Do I Need a Framework For This?

This is a question I have been asked many times, mainly by people who have not tried to build a complex Tool-based Application. The short answer is, to reduce (but sadly not eliminate) the chance that you will create an unholy disaster. But I’ll do a long one, too.

An important thing to understand about Tool-based applications is that as soon as you give users the option to use the Tools in any order, they will, and this will make everything much more complicated. In a View-based Application, the user is generally “On Rails”, in that the Application allows for doing X after Y but not before. When I start up the Twitter app, I can’t just jump directly to everything - I have to go through sequences of Views. This allows the developers of the Application to make vast assumptions about Application State. In particular, although Views might manipulate the same underlying DataModel (nearly always some form of database), I never have to worry about disambiguating a tap in one View from a tap in another. In some sense the Views are the Modes, and in the context of a particular View, there are generally only Commands, and not Tools.

As a result, in a View-based Application it is very easy to talk about Workflows. People creating View-based Applications tend to draw lots of diagrams that look like this:

These diagrams might be the Views themselves, but more often they are the steps a User would take through the Application - a User Story if you will. They are not always strictly linear, there can be branches and loops (a Google Image Search for Workflow has lots of more complex examples). But there are always well-defined entry and exit points. The User starts with a Task, and finishes with that Task completed, by way of the Workflow. It is then very natural to design an Application that provides the Workflow where the User can complete the Task. We can talk about Progress through the Workflow in a meaningful way, and the associated Data and Application State also make a kind of Progress. As additional Tasks are added, the job of the development team is to come up with a design that allows these necessary Workflows to be efficiently accomplished.

The fundamental complication in Content Creation/Editing Applications is that this methodology doesn’t apply to them at all. Ultimately the difference, I think, is that there is no inherent notion of Progress in a Content Creation/Editing Tool. For example, as a Powerpoint user, I can (and do!) spend hours re-organizing my slides, tweaking the image size and alignment, slightly adjusting text. In my mind I might have some nebulous notion of Progress, but this is not encoded in the Application. My Task is outside the Application. And without a clear Task or measure of Progress, there is no Workflow!

I think a more useful mental model for Content Creation/Editing Applications is like the image on the right. The green central hub the default state in these Applications, where generally you are just viewing your Content. For example Panning and Zooming your Image in Photoshop, or navigating around your 3D Scene in Blender. This is where the user spends a significant percentage of their time. The Blue spokes are the Tools. I go to a Tool for a while, but I always return to the Hub.

So if I were to track my state over time, it would be a winding path in and out of the default Hub, through untold numbers of Tools. There is no well-defined Order, as a user I am generally free to use the Tools in any Order I see fit. In a microcosm, we might be able to find small well-defined Workflows to analyze and optimize, but at the Application level, the Workflows are effectively infinite.

It might seem relatively obvious that the architectural approaches you need to take here are going to be different then in the Views approach. By squinting at it just the right way, one could argue that each Tool is basically a View, and so what is really different here? The difference, in my experience, is what I think of as Tool Sprawl.

If you have well-defined Workflows, then it is easy to make judgements about what is and isn’t necessary. Features that are extraneous to the required Workflows don’t just waste design and engineering time, they ultimately make the Workflows more complex than necessary - and that makes the User Experience worse! Modern software development orthodoxy is laser-focused on this premise - build the minimally viable product, and iterate, iterate, iterate to remove friction for the user.

Tool-based Applications are fundamentally different in that every additional Tool increases the value of the Application. If I have no use for a particular Tool, then except for the small UI overhead from the additional toolbar button necessary to launch the Tool, it’s addition hardly affects me at all. Of course, learning a new Tool will take some effort. But, the pay-off for that effort is this new Tool can now be combined with all the others! This leads to a sort of Application-level Network Effect, where each new Tool is a force-multiplier for all the existing Tools. This is immediately apparent if one observes virtually all major Content Creation/Editing Tools, where there are untold numbers of toolbars and menus of toolbars and nested tabs of toolbars, hidden behind other toolbars. To an outsider this looks like madness, but to the users, it’s the whole point.

Many people who come from the Workflow-oriented software world look upon these Applications in horror. I have observed many new projects where the team starts out trying to build something “simple”, that focuses on “core workflows”, perhaps for “novice users”, and lots of nice linear Workflow diagrams get drawn. But the reality is that Novice Users are only Novices until they have mastered your Application, and then they will immediately ask for more features. And so you will add a Tool here and there. And several years later you will have a sprawling set of Tools, and if you don’t have a systematic way to organize it all, you will have a mess on your hands.

Containing The Damage

Where does the mess come from? From what I have seen, there are a few very common ways to get in trouble. The first is just under-estimating the complexity of the task at hand. Many Content Creation Apps start out as “Viewers”, where all the app logic for things like 3D camera controls are done directly within the mouse and UI button handlers. Then over time new Editing functionality is incorporated by just adding more if/else branches or switch cases. This approach can carry on for quite a long time, and many 3D apps I have worked on still have these vestigial code-limbs at their core. But you’re just digging a deeper code-hole and filling it with code-spaghetti. Eventually, some actual software architecture will be needed, and painful refactoring efforts will be required (followed by years of fixing regressions, as users discover that all their favorite features are broken or work slightly differently now).

Even with some amount of “Tool Architecture”, how to handle device input is tricky, and often ends up leading to messy architectural lock-in. Given that “Tools” are often driven by device input, a seemingly-obvious approach is to directly give Tools input event handlers, like OnMouseUp/OnMouseMove/OnMouseDown functions. This becomes a natural place to put the code that “does things”, for example on a mouse event you might directly apply a brush stamp in a painting tool. Seems harmless until users ask for support for other input devices, like touch, or pen, or VR controllers. Now what? Do you just forward calls to your mouse handlers? What about pressure, or 3D position? And then comes automation, when users start asking for the ability to script what your Tool does. I have been in situations myself where “inject fake mouse event to force OnMouseX to run” started to seem like a viable solution (It is not. Absolutely not. Really, don’t).

Putting important code in input event handlers also leads to things like rampant copy-paste of standard event-handling patterns, which can be tedious to unwind if changes need to be made. And, expensive mouse event handlers will actually make your app feel less responsive than it ought to, due to something called mouse event priority. So, you really want to handle this part of your Tool Architecture carefully, because seemingly-standard design patterns can encourage a whole range of problems.

At the same time, if the Tools Architecture is too tightly defined, it can become a barrier to expanding the toolset, as new requirements come in that don’t “fit” the assumptions underlying the initial design. If many tools have been built on top of that initial architecture, it becomes intractable to change, and then clever Engineers are forced to come up with workarounds, and now you have two (or more) Tool Architectures. One of the biggest challenges is precisely how to divide up responsibilities between the Tool implementations and the Framework.

I can’t claim that the Interactive Tools Framework (ITF) will solve these problems for you. Ultimately, any successful software will end up being trapped by early design decisions, on top of which mountains have been built, and changing course can only happen at great expense. I could tell you stories all day, about how I have done this to myself. What I can say is, the ITF as realized in UE4 hopefully benefits from my past mistakes. Our experience with people using the ITF to build new Tools in the UE4 Editor over the past 2 years has (so far) been relatively painless, and we are continually looking for ways to smooth out any points of friction that do come up.

Tools, ToolBuilders, and the ToolManager

As I laid out above, an Interactive Tool is a Modal State of an Application, during which Device Input can be captured and interpreted in a specific way. In the Interactive Tools Framework (ITF), the UInteractiveTool base class represents the Modal State, and has a very small set of API functions that you are likely to need to implement. Below I have summarized the core UInteractiveTool API in psuedo-C++ (I have omitted things like virtual, const, optional arguments, etc, for brevity). There are other sets of API functions that we will cover to some extent later, but these are the critical ones. You initialize your Tool in ::Setup(), and do any finalization and cleanup in ::Shutdown(), which is also where you would do things like an ‘Apply’ operation. EToolShutdownType is related to the HasAccept() and CanAccept() functions, I will explain more below. Finally a Tool will be given a chance to Render() and Tick each frame. Note that there is also a ::Tick() function, but you should override ::OnTick() as the base class ::Tick() has critical functionality that must always run.

UCLASS()
class UInteractiveTool : public UObject, public IInputBehaviorSource
{
    void Setup();
    void Shutdown(EToolShutdownType ShutdownType);
    void Render(IToolsContextRenderAPI* RenderAPI);
    void OnTick(float DeltaTime);

    bool HasAccept();
    bool CanAccept();
};

A UInteractiveTool is not a standalone object, you cannot simply spawn one yourself. For it to function, something must call Setup/Render/Tick/Shutdown, and pass appropriate implementations of things like the IToolsContextRenderAPI, which allow the Tool to draw lines/etc. I will explain further below. But for now what you need to know is, to create a Tool instance, you will need to request one from a UInteractiveToolManager. To allow the ToolManager to build arbitrary types, you register a <String, UInteractiveToolBuilder> pair with the ToolManager. The UInteractiveToolBuilder is a very simple factory-pattern base class that must be implemented for each Tool type:

UCLASS()
class UInteractiveToolBuilder : public UObject
{
    bool CanBuildTool(const FToolBuilderState& SceneState);
    UInteractiveTool* BuildTool(const FToolBuilderState& SceneState);
};

The main API for UInteractiveToolManager is summarized below. Generally you will not need to implement your own ToolManager, the base implementation is fully functional and should do everything required to use Tools. But you are free to extend the various functions in a subclass, if necessary.

The functions below are listed in roughly the order you would call them. RegisterToolType() associates the string identifier with a ToolBuilder implementation. The Application then sets an active Builder using SelectActiveToolType(), and then ActivateTool() to create a new UInteractiveTool instance. There are getters to access the active Tool, but there is rarely call to do this frequently, in practice. The Render() and Tick() functions must be called each frame by the Application, which then call the associated functions for the active Tool. Finally DeactiveTool() is used to terminate the active Tool.

UCLASS()
class UInteractiveToolManager : public UObject, public IToolContextTransactionProvider
{
    void RegisterToolType(const FString& Identifier, UInteractiveToolBuilder* Builder);
    bool SelectActiveToolType(const FString& Identifier);
    bool ActivateTool();

    void Tick(float DeltaTime);
    void Render(IToolsContextRenderAPI* RenderAPI);

    void DeactivateTool(EToolShutdownType ShutdownType);
};

Tool Life Cycle

At the high level, the Life Cycle of a Tool is as follows

1. ToolBuilder is registered with ToolManager

2. Some time later, User indicates they wish to start Tool (eg via button)

3. UI code sets Active ToolBuilder, Requests Tool Activation

4. ToolManager checks that ToolBuilder.CanBuildTool() = true, if so, calls BuildTool() to create new instance

5. ToolManager calls Tool Setup()

6. Until Tool is deactivated, it is Tick()’d and Render()’d each frame

7. User indicates they wish to exit Tool (eg via button, hotkey, etc)

8. ToolManager calls Tool Shutdown() with appropriate shutdown type

9. Some time later, Tool instance is garbage collected

Note the last step. Tools are UObjects, so you cannot rely on the C++ destructor for cleanup. You should do any cleanup, such as destroying temporary actors, in your Shutdown() implementation.

EToolShutdownType and the Accept/Cancel Model

A Tool can support termination in two different ways, depending on what type of interactions the Tool supports. The more complex alternative is a Tool which can be Accepted (EToolShutdownType::Accept) or Cancelled (EToolShutdownType::Cancel). This is generally used when the Tool’s interaction supports some kind of live preview of an operation, that the user may wish to discard. For example, a Tool that applies a mesh simplification algorithm to a selected Mesh likely has some parameters the user may wish to explore, but if the exploration is unsatisfactory, the user may prefer to not apply the simplification at all. In this case, the UI can provide buttons to Accept or Cancel the active Tool, which result in calls to ToolManager::DeactiveTool() with the appropriate EToolShutdownType value.

The second termination alternative - EToolShutdownType::Completed - is simpler in that it simply indicates that the Tool should “exit”. This type of termination can be used to handle cases where there is no clear ‘Accept’ or ‘Cancel’ action, for example in Tools that simply visualize data, Tools where editing operations are applied incrementally (eg spawning objects based on click points), and so on.

To be clear, you do not need to use or support Accept/Cancel-style Tools in your usage of the ITF. Doing so generally results in a more complex UI. And if you support Undo in your application, then even Tools that could have Accept and Cancel options, can equivalently be done as Complete-style Tools, and the user can Undo if they are unhappy. However, if the Tool completion can involve lengthy computations or is destructive in some way, supporting Accept/Cancel tends to result in a better user experience. In the UE Editor’s Modeling Mode, we generally use Accept/Cancel when editing Static Mesh Assets for precisely this reason.

Another decision you will have to make is how to handle the modal nature of Tools. Generally it is useful to think of the user as being “in” a Tool, ie in the particular Modal state. So how do they get “out”? You can require the user to explicitly click Accept/Cancel/Complete buttons to exit the active Tool, this is the simplest and most explicit, but does mean clicks are necessary, and the user has to mentally be aware of and manage this state. Alternately you could automatically Accept/Cancel/Complete when the user selects another Tool in the Tool toolbar/menu/etc (for example). However this raises a thorny issue of whether one should auto-Accept or auto-Cancel. There is no right answer to this question, you must decide what is best for your particular context (although in my experience, auto-Cancelling is can be quite frustrating when one accidentally mis-clicks!)

Base Tools

One of the main goals of the ITF is to reduce the amount of boilerpate code necessary to write Tools, and improve consistency. Several “tool patterns” come up so frequently that we have included standard implementations of them in the ITF, in the /BaseTools/ subfolder. Base Tools generally include one or more InputBehaviors (see below), whose actions are mapped to virtual functions you can override and implement. I will briefly describe each of these Base Tools as they are both a useful way to build your own Tools, and a good source of sample code for how to do things:

USingleClickTool captures mouse-click input and, if the IsHitByClick() function returns a valid hit, calls OnClicked() function. You provide implementations of both of these. Note that the FInputDeviceRay structure here includes both a 2D mouse position, and 3D ray.

class INTERACTIVETOOLSFRAMEWORK_API USingleClickTool : public UInteractiveTool
{
    FInputRayHit IsHitByClick(const FInputDeviceRay& ClickPos);
    void OnClicked(const FInputDeviceRay& ClickPos);
};

UClickDragTool captures and forwards continuous mouse, input instead of a single click. If CanBeginClickDragSequence() returns true (generally you would do a hit-test here, similar to USingleClickTool), then OnClickPress() / OnClickDrag() / OnClickRelease() will be called, similar to standard OnMouseDown/Move/Up event patterns. Note, however, that you must handle the case where the sequence aborts without a Release, in OnTerminateDragSequence().

class INTERACTIVETOOLSFRAMEWORK_API UClickDragTool : public UInteractiveTool
{
    FInputRayHit CanBeginClickDragSequence(const FInputDeviceRay& PressPos);
    void OnClickPress(const FInputDeviceRay& PressPos);
    void OnClickDrag(const FInputDeviceRay& DragPos);
    void OnClickRelease(const FInputDeviceRay& ReleasePos);
    void OnTerminateDragSequence();
};

UMeshSurfacePointTool is similar to UClickDragTool in that it provides a click-drag-release input handling pattern. However, UMeshSurfacePointTool assumes that it is acting on a target UPrimitiveComponent (how it gets this Component will be explained below). The default implementation of the HitTest() function below will use standard LineTraces (so you don’t have to override this function if that is sufficient). UMeshSurfacePointTool also supports Hover, and tracks the state of Shift and Ctrl modifier keys. This is a good starting point for simple “draw-on-surface” type tools, and many of the Modeling Mode Tools derive from UMeshSurfacePointTool. (One small note: this class also supports reading stylus pressure, however in UE4.26 stylus input is Editor-Only) ((Extra Note: Although it is named UMeshSurfacePointTool, it does not actually require a Mesh, just a UPrimitiveComponent that supports a LineTrace))

class INTERACTIVETOOLSFRAMEWORK_API UMeshSurfacePointTool : public UInteractiveTool
{
    bool HitTest(const FRay& Ray, FHitResult& OutHit);
    void OnBeginDrag(const FRay& Ray);
    void OnUpdateDrag(const FRay& Ray);
    void OnEndDrag(const FRay& Ray);

    void OnBeginHover(const FInputDeviceRay& DevicePos);
    bool OnUpdateHover(const FInputDeviceRay& DevicePos);
    void OnEndHover();
};

There is a fourth Base Tool, UBaseBrushTool, that extends UMeshSurfacePointTool with various functionality specific to Brush-based 3D Tool, ie a surface painting brush, 3D sculpting tool, and so on. This includes a set of standard brush properties, a 3D brush position/size/falloff indicator, tracking of “brush stamps”, and various other useful bits. If you are building brush-style Tools, you may find this useful.

FToolBuilderState

The UInteractiveToolBuilder API functions both take a FToolBuilderState argument. The main purpose of this struct is to provide Selection information - it indicates what the Tool would or should act on. Key fields of the struct are shown below. The ToolManager will construct a FToolBuilderState and pass it to the ToolBuilders, which will then use it to determine if they can operate on the Selection. Both Actors and Components can be passed, but also only Actors and Components, in the UE4.26 ITF implementation. Note that if a Component appears in SelectedComponents, then it’s Actor will be in SelectedActors. The UWorld containing these Actors is also included.

struct FToolBuilderState
{
    UWorld* World;
    TArray<AActor*> SelectedActors;
    TArray<UActorComponent*> SelectedComponents;
};

In the Modeling Mode Tools, we do not directly operate on Components, we wrap them in an standard container, so that we can, for example, 3D sculpt “any” mesh Component that has a container implementation. This is largely why I can write this tutorial, because I can make those Tools edit other types of meshes, like Runtime meshes. But when building your own Tools, you are free to ignore FToolBuilderState. Your ToolBuilders can use any other way to query scene state, and your Tools are not limited to acting on Actors or Components.

On ToolBuilders

A frequent question that comes up among users of the ITF is whether the UInteractiveToolBuilder is necessary. In the simplest cases, which are the most common, your ToolBuilder will be straightforward boilerplate code (unfortunately since it is a UObject, this boilerplate cannot be directly converted to a C++ template). The utility of ToolBuilders arises when one starts to re-purpose existing UInteractiveTool implementations to solve different problems.

For example, in the UE Editor we have a Tool for editing mesh polygroups (effectively polygons), called PolyEdit. We also have a very similar tool for editing mesh triangles, called TriEdit. Under the hood, these are the same UInteractiveTool class. In TriEdit mode, the Setup() function configures various aspects of the Tool to be appropriate for triangles. To expose these two modes in the UI, we use two separate ToolBuilders, which set a “bIsTriangleMode” flag on the created Tool instance after it is allocated, but before Setup() runs.

I certainly won’t claim this is an elegant solution. But, it was expedient. In my experience, this situation arises all the time as your set of Tools evolves to handle new situations. Frequently an existing Tool can be shimmed in to solve a new problem with a bit of custom initialization, a few additional options/properties, and so on. In an ideal world one would refactor the Tool to make this possible via subclassing or composition, but we rarely live in the ideal world. So, the bit of unsightly code necessary to hack a Tool to do a second job, can be placed in a custom ToolBuilder, where it is (relatively) encapsulated.

The string-based system for registering ToolBuilders with the ToolManager can allow your UI level (ie button handlers and so on) to launch Tools without having to actually know about the Tool class types. This can often allow for a cleaner separation of concerns when building the UI. For example, in the ToolsFrameworkDemo I will describe below, the Tools are launched by UMG Blueprint Widgets that simply pass string constants to a BP Function - they have no knowledge of the Tool system at all. However, the need to set an ‘Active’ builder before spawning a Tool is somewhat of a vestigial limb, and these operations will likely be combined in the future.

The Input Behavior System

Above I stated that “An Interactive Tool is a Modal State of an Application, during which Device Input can be captured and interpreted in a specific way”. But the UInteractiveTool API does not have any mouse input handler functions. This is because Input Handling is (mostly) decoupled from the Tools. Input is captured and interpreted by UInputBehavior objects that the Tool creates and registers with the UInputRouter, which “owns” the input devices and routes input events to the appropriate Behavior.

The reason for this separation is that the vast majority of input handling code is cut-and-pasted, with slight variations in how particular interactions are implemented. For example consider a simple button-click interaction. In a common event API you would have something like OnMouseDown(), OnMouseMove(), and OnMouseUp() functions that can be implemented, and lets say you want to map from those events to a single OnClickEvent() handler, for a button press-release action. A surprising number of applications (particularly web apps) will fire the click in OnMouseDown - which is wrong! But, blindly firing OnClickEvent in OnMouseUp is also wrong! The correct behavior here is actually quite complex. In OnMouseDown(), you must hit-test the button, and begin capturing mouse input. In OnMouseUp, you have to hit-test the button again, and if the cursor is still hitting the button, only then is OnClickEvent fired. This allows for cancelling a click and is how all serious UI toolkits have it implemented (try it!).

If you have even tens of Tools, implementing all this handling code, particularly for multiple devices, becomes very error-prone. So for this reason, the ITF moves these little input-event-handling state machines into UInputBehavior implementations which can be shared across many tools. In fact a few simple behaviors like USingleClickInputBehavior, UClickDragBehavior, and UHoverBehavior handle the majority of cases for mouse-driven interaction. The Behaviors then forward their distilled events to target objects via simple interfaces that something like a Tool or Gizmo can implement. For example USingleClickInputBehavior can act on anything that implemments IClickBehaviorTarget, which just has two functions - IsHitByClick() and OnClicked(). Note that because the InputBehavior doesn’t know what it is acting on - the “button” could be a 2D rectangle or an arbitrary 3D shape - the Target interface has to provide the hit-testing functionality.

Another aspect of the InputBehavior system is that Tools do not directly talk to the UInputRouter. They only provide a list of UInputBehavior’s that they wish to have active. The additions to the UInteractiveTool API to support this are shown below. Generally, in a Tool’s ::Setup() implementation, one or more Input Behaviors are created and configured, and passed to AddInputBehavior. The ITF then calls GetInputBehaviors when necessary, to register those behaviors with the UInputRouter. Note: currently the InputBehavior set cannot change dynamically during the Tool, however you can configure your Behaviors to ignore events based on whatever criteria you wish.

class UInteractiveTool : public UObject, public IInputBehaviorSource
{
    // ...previous functions...

    void AddInputBehavior(UInputBehavior* Behavior);
    const UInputBehaviorSet* GetInputBehaviors();
};

The UInputRouter is similar to the UInteractiveToolManager in that the default implementation is sufficient for most usage. The only job of the InputRouter is to keep track of all the active InputBehaviors and mediate capture of the input device. Capture is central to input handling in Tools. When a MouseDown event comes into the InputRouter, it checks with all the registered Behaviors to ask if they want to start capturing the mouse event stream. For example if you press down over a button, that button’s registered USingleClickInputBehavior would indicate that yes, it wants to start capturing. Only a single Behavior is allowed to capture input at a time, and multiple Behaviors (which don’t know about eachother) might want to capture - for example, 3D objects that are overlapping from the current view. So, each Behavior returns a FInputCaptureRequest that indicates “yes” or “no” along with depth-test and priority information. The UInputRouter then looks at all the capture requests and, based on depth-sorting and priority, selects one Behavior and tells it that capture will begin. Then MouseMove and MouseRelease events are only passed to that Behavior until the Capture terminates (usually on MouseRelease).

In practice, you will rarely have to interact with UInputRouter when using the ITF. Once the connection between application-level mouse events and the InputRouter is established, you shouldn’t ever need to touch it again. This system largely deals away with common errors like mouse handling “getting stuck” due to a capture gone wrong, because the UInputRouter is ultimately in control of mouse capture, not individual Behaviors or Tools. In the accompanying ToolsFrameworkDemo project, I have implemented everything necessary for the UInputRouter to function.

The basic UInputBehavior API is shown below. The FInputDeviceState is a large structure that contains all input device state for a given event/time, including status of common modifier keys, mouse button state, mouse position, and so on. One main difference from many input events is that the 3D World-Space Ray associated with the input device position is also included.

UCLASS()
class UInputBehavior : public UObject
{
    FInputCapturePriority GetPriority();
    EInputDevices GetSupportedDevices();

    FInputCaptureRequest WantsCapture(const FInputDeviceState& InputState);
    FInputCaptureUpdate BeginCapture(const FInputDeviceState& InputState);
    FInputCaptureUpdate UpdateCapture(const FInputDeviceState& InputState);
    void ForceEndCapture(const FInputCaptureData& CaptureData);

    // ... hover support...
}

I have omitted some extra parameters in the above API, to simplify things. In particular if you implement your own Behaviors, you will discover there is an EInputCaptureSide enum passed around nearly everywhere, largely as a default EInputCaptureSide::Any. This is for future use, to support the situation where a Behavior might be specific to a VR controller in either hand.

However, for most apps you will likely find that you never actually have to implement your own Behavior. A set of standard behaviors, such as those mentioned above, is included in the /BaseBehaviors/ folder of the InteractiveToolFramework module. Most of the standard Behaviors are derived from a base class UAnyButtonInputBehavior, which allows them to work with any mouse button, including “custom” buttons defined by a TFunction (which could be a keyboard key)! Similarly the standard BehaviorTarget implementations all derive from IModifierToggleBehaviorTarget, which allows for arbitrary modifier keys to be configured on a Behavior and forwarded to the Target without having to subclass or modify the Behavior code.

Direct Usage of UInputBehaviors

In the discussion above, I focused on the case where a UInteractiveTool provides a UInputBehaviorSet. Gizmos will work similarly. However, the UInputRouter itself is not aware of Tools at all, and it is entirely possible to use the InputBehavior system separately from either. In the ToolsFrameworkDemo, I implemented the click-to-select-meshes interaction this way, in the USceneObjectSelectionInteraction class. This class implements IInputBehaviorSource and IClickBehaviorTarget itself, and is just owned by the framework back-end subsystem. Even this is not strictly necessary - you can directly register a UInputBehavior you create yourself with the UInputRouter (note, however, that due to an API oversight on my part, in UE4.26 you cannot explicitly unregister a single Behavior, you can only unregister by source).

Non-Mouse Input Devices

Additional device types are currently not handled in the UE4.26 ITF implementation, however the previous iteration of this behavior system in frame3Sharp supported touch and VR controller input, and these should (eventually) work similarly in the ITF design. The general idea is that only the InputRouter and Behaviors need to explicitly know about different input modalities. An IClickBehaviorTarget implementation should work similarly with a mouse button, finger tap, or VR controller click, but also nothing rules out additional Behavior Targets tailored for device-specific interactions (eg from a two-finger pinch, spatial controller gesture, and so on). Tools can register different Behaviors for different device types, the InputRouter would take care of handling which devices are active and capturable.

Currently, some level of handling of other device types can be accomplished by mapping to mouse events. Since the InputRouter does not directly listen to the input event stream, but rather the ITF back-end creates and forwards events, this is a natural place to do such mappings, some more detail will be explained below.

A Limitation - Capture Interruption

One limitation of this system which is important to be aware of when designing your interactions is that “interruption” of an active capture is not yet supported by the framework. This most frequently arises when one wishes to have an interaction that would either be a click, or a drag, depending on if the mouse is immediately released in the same location, or moved some threshold distance. In simple cases this can be handled via UClickDragBehavior, with your IClickDragBehaviorTarget implementation making the determination. However, if the click and drag actions need to go to very different places that are not aware of eachother, this may be painful. A cleaner way to support this kind of interaction is to allow one UInputBehavior to “interrupt” another - in this case, the drag to “interrupt” the click’s active capture when it’s preconditions (ie sufficient mouse movement) are met. This is an area of the ITF that may be improved in the future.

Tool Property Sets

UInteractiveTool has one other set of API functions that I haven’t covered, which is for managing a set of attached UInteractiveToolPropertySet objects. This is a completely optional system that is somewhat tailored for usage in the UE Editor. For Runtime usage it is less effective. Essentially UInteractiveToolPropertySet’s are for storing your Tool Settings and Options. They are UObjects with UProperties, and in the Editor, these UObjects can be added to a Slate DetailsView to automatically expose those properties in the Editor UI.

The additional UInteractiveTool APIs are summarized below. Generally in the Tool ::Setup() function, various UInteractiveToolPropertySet subclasses will be created and passed to AddToolPropertySource(). The ITF back-end will use the GetToolProperties() function to initialize the DetailsView panel, and then the Tool can show and hide property sets dynamically using SetToolPropertySourceEnabled()

class UInteractiveTool : public UObject, public IInputBehaviorSource
{
    // ...previous functions...
public:
    TArray<UObject*> GetToolProperties();
protected:
    void AddToolPropertySource(UObject* PropertyObject);
    void AddToolPropertySource(UInteractiveToolPropertySet* PropertySet);
    bool SetToolPropertySourceEnabled(UInteractiveToolPropertySet* PropertySet, bool bEnabled);
};

In the UE Editor, UProperties can be marked up with meta tags to control the generated UI widgets - things like slider ranges, valid integer values, and enabling/disabling widgets based on the value of other properties. Much of the UI in the Modeling Mode works this way.

Unfortunately, UProperty meta tags are not available at Runtime, and the DetailsView panels are not supported in UMG Widgets. As a result, the ToolPropertySet system becomes much less compelling. It does still provide some useful functionality though. For one, the Property Sets support saving and restoring their Settings across Tool invocations, using the SaveProperties() and RestoreProperties() functions of the property set. You simply call SaveProperties() on each property set in your Tool Shutdown(), and RestoreProperties() in ::Setup().

A second useful ability is the WatchProperty() function, which allows for responding to changes in PropertySet values without any kind of change notification. This is necessary with UObjects because C++ code can change a UProperty on a UObject directly, and this will not cause any kind of change notification to be sent. So, the only way to reliably detect such changes is via polling. Yes, polling. It’s not ideal, but do consider that (1) a Tool necessarily has a limited number of properties that a user can possibly handle and (2) only one Tool is active at a time. To save you from having to implement a stored-value-comparison for each property in your ::OnTick(), you can add watchers using this pattern:

MyPropertySet->WatchProperty( MyPropertySet->bBooleanProp,  [this](bool bNewValue) { // handle change! } );

In UE4.26 there are some additional caveats (read: bugs) that must be worked around, see below for more details.

Tool Actions

Finally, the last major part of the UInteractiveTool API is support for Tool Actions. These are not widely used in the Modeling Mode toolset, except to implement hotkey functionality. However, the Tool Actions are not specifically related to hotkeys. What they allow is for a Tool to expose “Actions” (ie parameterless functions) that can be called via integer identifiers. The Tool constructs and returns a FInteractiveToolActionSet, and then higher-level client code can enumerate these actions, and execute them using the ExecuteAction function defined below.

class UInteractiveTool : public UObject, public IInputBehaviorSource
{
    // ...previous functions...
public:
    FInteractiveToolActionSet* GetActionSet();
    void ExecuteAction(int32 ActionID);
protected:
    void RegisterActions(FInteractiveToolActionSet& ActionSet);
};

The sample code below shows two Tool Actions being registered. Note that although the FInteractiveToolAction contains a hotkey and modifier, these are only suggestions to the higher-level client. The UE Editor queries Tools for Actions, and then registers the suggested hotkeys as Editor hotkeys, which allows the user to remap them. UE does not have any kind of similar hotkey system at Runtime, you would need to manually map these hotkeys yourself

void UDynamicMeshSculptTool::RegisterActions(FInteractiveToolActionSet& ActionSet)
{
    ActionSet.RegisterAction(this, (int32)EStandardToolActions::BaseClientDefinedActionID + 61,
        TEXT("SculptDecreaseSpeed"),
        LOCTEXT("SculptDecreaseSpeed", "Decrease Speed"),
        LOCTEXT("SculptDecreaseSpeedTooltip", "Decrease Brush Speed"),
        EModifierKey::None, EKeys::W,
        [this]() { DecreaseBrushSpeedAction(); });

    ActionSet.RegisterAction(this, (int32)EStandardToolActions::ToggleWireframe,
        TEXT("ToggleWireframe"),
        LOCTEXT("ToggleWireframe", "Toggle Wireframe"),
        LOCTEXT("ToggleWireframeTooltip", "Toggle visibility of wireframe overlay"),
        EModifierKey::Alt, EKeys::W,
        [this]() { ViewProperties->bShowWireframe = !ViewProperties->bShowWireframe; });
}

Ultimately each ToolAction payload is stored as a TFunction<void()>. If you are just forwarding to another Tool function, like the DecreaseBrushSpeedAction() call above, you don’t necessarily benefit from the ToolAction system, and there is no need to use it at all. However due to current limitations with Tool exposure to Blueprints, ToolActions (because they can be called via a simple integer) may be an effective way to expose Tool functionality to BP without having to write many wrapper functions.

Gizmos

As I have mentioned, “Gizmo” refers to those little in-viewport clicky-things we use in 2D and 3D Content Creation/Editing Apps to let you efficiently manipulate parameters of visual elements or objects. If you’ve used any 3D tool, you have almost certainly used a standard Translate/Rotate/Scale Gizmo, for example. Like Tools, Gizmos capture user input, but instead of being a full Modal state, a Gizmo is generally transient, ie Gizmos can come and go, and you can have multiple Gizmos active at the same time, and they only capture input if you click “on” them (what “on” means can be a bit fuzzy). Because of this, Gizmos generally require some specific visual representation that allows the user to indicate when they want to “use” the Gizmo, but conceptually you can also have a Gizmo that does this based on a hotkey or application state (eg checkbox).

In the Interactive Tools Framework, Gizmos are implemented as subclasses of UInteractiveGizmo, which is very similar to UInteractiveTool:

UCLASS()
class UInteractiveGizmo : public UObject, public IInputBehaviorSource
{
    void Setup();
    void Shutdown();
    void Render(IToolsContextRenderAPI* RenderAPI);
    void Tick(float DeltaTime);

    void AddInputBehavior(UInputBehavior* Behavior);
    const UInputBehaviorSet* GetInputBehaviors();
}

And similarly Gizmo instances are managed by a UInteractiveGizmoManager, using UInteractiveGizmoBuilder factories registered via strings. Gizmos use the same UInputBehavior setup, and are similarly Rendered and be Ticked every frame by the ITF.

At this high level, the UInteractiveGizmo is just a skeleton, and to implement a custom Gizmo you will have to do quite a bit of work yourself. Unlike Tools, it’s more challenging to provide “base” Gizmos because of the visual-representation aspect. In particular, the standard InputBehaviors will require that you are able to do raycast hit-testing against your Gizmo, and so you can’t just draw arbitrary geometry in the Render() function. That said, the ITF does provide a very flexible standard Translate-Rotate-Scale Gizmo implementation, which can be repurposed to solve many problems.

Standard UTransformGizmo

It would be very questionable to call the ITF a framework for building 3D tools if it didn’t include standard Translate-Rotate-Scale (TRS) Gizmos. What is currently available in UE4.26 is a combined TRS gizmo (screenshot to the right) called UTransformGizmo that supports Axis and Plane Translation (axis lines and central chevrons), Axis rotation (circles), Uniform Scale (central box), Axis Scale (outer axis brackets), and Plane Scale (outer chevrons). These sub-gizmos are separately configurable, so you can (for example) create a UTransformGizmo instance that only has XY-plane translation and Z rotation just by passing certain enum values to the Gizmo builder.

This TRS Gizmo is not a single monolithic Gizmo, it is built up out of a set of parts that can be repurposed for many other uses. This subsystem is complex enough that it warrants a separate article, but to summarize, each element of the UTransformGizmo that I mentioned above is actually a separate UInteractiveGizmo (so, yes, you can have nested/hierarchical Gizmos, and you could subclass UTransformGizmo to add additional custom controls). For example, the axis-translation sub-gizmos (drawn as the red/green/blue line segments) are instances of UAxisPositionGizmo, and the rotation circles are UAxisAngleGizmo.

The sub-gizmos like UAxisPositionGizmo do not explicitly draw the lines in the image above. They are instead connected to an arbitrary UPrimitiveComponent which provides the visual representation and hit-testing. So, you could use any UStaticMesh, if you wished. By default, UTransformGizmo spawns custom gizmo-specific UPrimitiveComponents, in the case of the lines, it is a UGizmoArrowComponent. These GizmoComponents provide some niceties like constant screen-space dimensions, hover support, and so on. But you absolutely do not have to use them, and the Gizmo look could be completely customized for your purposes (a topic for a future Gizmo-focused article!).

So, the UAxisPositionGizmo is really just an implementation of the abstract concept of “specifying position along a line based on mouse input”. The 3D line, mapping from line position to abstract parameter (in the default case, 3D world position), and state-change information are all implemented via UInterfaces and so can be customized if necessary. The visual representation is only to inform the user, and to provide a hit-target for the InputBehavior that captures the mouse. This allows functionality like arbitrary Snapping or parameter constraints to be integrated with minimal difficultly.

But, this is all an aside. In practice, to use a UTransformGizmo, you just request one from the GizmoManager using one of the following calls:

class UInteractiveGizmoManager 
{
    // ... 
    UTransformGizmo* Create3AxisTransformGizmo(void* Owner);
    UTransformGizmo* CreateCustomTransformGizmo(ETransformGizmoSubElements Elements, void* Owner);
}

Then you create a UTransformProxy instance and set it as the Target of the Gizmo. The Gizmo will now be fully functional, you can move it around the 3D scene, and respond to transform changes via the UTransformProxy::OnTransformChanged delegate. Various other delegates are available, eg for begin/end a transform interaction. Based on these delegates, you could transform objects in your scene, update parameters of an object, and so on.

A slightly more complex usage is if you want the UTransformProxy to directly move one or more UPrimitiveComponents, ie to implement the normal “select objects and move them with gizmo” type of interface that nearly every 3D design app has. In this case the Components can be added as targets of the Proxy. The Gizmo still acts on the UTransformProxy, and the Proxy re-maps that single transform to relative transforms on the object set.

The UTransformGizmo does not have to be owned by a Tool. In the ToolsFrameworkDemo, the USceneObjectTransformInteraction class watches for selection changes in the runtime objects Scene, and if there is an active selection, spawns a suitable new UTransformGizmo. The code is only a handful of lines:

TransformProxy = NewObject<UTransformProxy>(this);
for (URuntimeMeshSceneObject* SceneObject : SelectedObjects)
{
    TransformProxy->AddComponent(SO->GetMeshComponent());
}

TransformGizmo = GizmoManager->CreateCustomTransformGizmo(ETransformGizmoSubElements::TranslateRotateUniformScale, this);
TransformGizmo->SetActiveTarget(TransformProxy);

In this case I am passing ETransformGizmoSubElements::TranslateRotateUniformScale to create TRS gizmos that do not have the non-uniform scaling sub-elements. To destroy the gizmo, the code simply calls DestroyAllGizmosByOwner, passing the same void* pointer used during creation:

GizmoManager->DestroyAllGizmosByOwner(this);

The UTransformGizmo automatically emits the necessary undo/redo information, which will be discussed further below. So as long as the ITF back-end in use supports undo/redo, so will the gizmo transformations.

Local vs Global Coordinate Systems

The UTransformGizmo supports both local and global coordinate systems. By default, it requests the current Local/Global setting from the ITF back-end. In the UE Editor, this is controlled in the same way as the default UE Editor gizmos, by using the same world/local toggle at the top of the main viewport. You can also override this behavior, see the comments in the UTransformGizmoBuilder header.

One caveat, though. UE4 only supports non-uniform scaling transformations in the local coordinate-system of a Component. This is because two separate FTransform’s with non-uniform scaling cannot be combined into a single FTransform, in most cases. So, when in Global mode, the TRS Gizmo will not show the non-uniform scaling handles (the axis-brackets and outer-corner chevrons). The default UE Editor Gizmos have the same limitation, but handle it by only allowing usage of the Local coordinate system in the scaling Gizmo (which is not combined with the translate and rotate Gizmos).

The Tools Context and ToolContext APIs

At this point we have Tools and a ToolManager, and Gizmos and a GizmoManager, but who manages the Managers? Why, the Context of course. UInteractiveToolsContext is the topmost level of the Interactive Tools Framework. It is essentially the “universe” in which Tools and Gizmos live, and also owns the InputRouter. By default, you can simply use this class, and that’s what I’ve done in the ToolsFrameworkDemo. In the UE Editor usage of the ITF, there are subclasses that mediate the communication between the ITF and higher-level Editor constructs like an FEdMode (for example see UEdModeInteractiveToolsContext).

The ToolsContext also provides the Managers and InputRouter with implementations of various APIs that provide “Editor-like” functionality. The purpose of these APIs is to essentially provide an abstraction of an “Editor”, which is what has allowed us to prevent the ITF from having explicit Unreal Editor dependencies. In the text above I have mentioned the “ITF back-end” multiple times - this is what I was referring to.

If it’s still not clear what I mean by an “abstraction of an Editor”, perhaps an example. I have not mentioned anything about object Selections yet. This is because the concept of selected objects is largely outside the scope of the ITF. When the ToolManager goes to construct a new Tool, it does pass a list of selected Actors and Components. But it gets this list by asking the Tools Context. And the Tools Context doesn’t know, either. The Tools Context needs to ask the Application that created it, via the IToolsContextQueriesAPI. This surrounding Application must create an implementation of IToolsContextQueriesAPI and pass it to the ToolsContext on construction.

The ITF cannot solve “how object selection works” in a generic way because this is highly dependent on your Application. In the ToolsFrameworkDemo I have implemented a basic mesh-objects-and-selection-list mechanism, that behaves similarly to most DCC tools. The Unreal Editor has a similar system in the main viewport. However, in Asset Editors, there is only ever a single object, and there is no selection at all. So the IToolsContextQueriesAPI used inside Asset Editors is different. And if you were using the ITF in a game context, you likely will have a very different notion of what “selection” is, or even what “objects” are.

So, our goal with the ToolContext APIs is to require the minimal set of functions that allow Tools to work within “an Editor-like container”. These APIs have grown over time as new situations arise where the Editor-container needs to be queried. They are defined in the file ToolContextInterfaces.h and summarized below

IToolsContextQueriesAPI

This API provides functions to query state information from the Editor container. The most critical is GetCurrentSelectionState(), which will be used by the ToolManager to determine which selected actors and Components to pass to the ToolBuilders. You will likely need to have a custom implementation of this in your usage of the ITF. GetCurrentViewState() is also required for many Tools to work correctly, and for the TRS Gizmos, as it provides the 3D camera/view information. However the sample implementation in the ToolsFrameworkDemo is likely sufficient for any Runtime use that is a standard fullscreen single 3D view. The other functions here can have trivial implementations that just return a default value.

class IToolsContextQueriesAPI
{
    void GetCurrentSelectionState(FToolBuilderState& StateOut);
    void GetCurrentViewState(FViewCameraState& StateOut);
    EToolContextCoordinateSystem GetCurrentCoordinateSystem();
    bool ExecuteSceneSnapQuery(const FSceneSnapQueryRequest& Request, TArray<FSceneSnapQueryResult>& Results );
    UMaterialInterface* GetStandardMaterial(EStandardToolContextMaterials MaterialType);
}

IToolsContextTransactionsAPI

The IToolsContextTransactionsAPI is mainly used to send data back to the Editor container. DisplayMessage() is called by Tools with various user-informative messages, error and status messages, and so on. These can be ignored if preferred. PostInvalidation() is used to indicate that a repaint is necessary, which is generally can be ignored in a Runtime context where the engine is continually redrawing at maximum/fixed framerate. RequestSelectionChange() is a hint certain Tools provide, generally when they create a new object, and can be ignored.

class IToolsContextTransactionsAPI
{
    void DisplayMessage(const FText& Message, EToolMessageLevel Level);
    void PostInvalidation();
    bool RequestSelectionChange(const FSelectedOjectsChangeList& SelectionChange);

    void BeginUndoTransaction(const FText& Description);
    void AppendChange(UObject* TargetObject, TUniquePtr<FToolCommandChange> Change, const FText& Description);
    void EndUndoTransaction();
}

AppendChange() is called by Tools that want to emit a FCommandChange record (actually a FToolCommandChange subclass), which is the core component of the ITF approach to Undo/Redo. To understand why this design is the way it is, I have to explain about about how Undo/Redo works in the UE Editor. The Editor does not use a Command-Objects/Pattern approach to Undo/Redo, which is generally the way that most 3D Content Creation/Editing Tools do it. Instead the Editor uses a Transaction system. After opening a Transaction, UObject::Modify() is called on any object that is about to be modified, and this saves a copy of all the UObject’s current UProperty values. When the Transaction is closed, the UProperties of modified objects are compared, and any changes are serialized. This system is really the only way to do it for something like UObjects, that can have arbitrary user-defined data via UProperties. However, Transaction systems are known to not perform well when working with large complex data structures like meshes. For example, storing arbitrary partial changes to a huge mesh as a Transaction would involve making a full copy up front, and then searching for and encoding changes to the complex mesh data structures (essentially unstructured graphs). This is very difficult (read: slow) computational problem. Similarly a simple 3D translation will modify every vertex, requiring a full copy of all the position data in a Transaction, but in a Change can be stored as just the translation vector and a bit if information about what operation to apply.

So, when building the ITF, we added support for embedding FCommandChange objects inside UE Editor Transactions. This is a bit of a kludge, but generally works, and a useful side-effect is that these FCommandChanges can also be used at Runtime, where the UE Editor Transaction system does not exist. Most of our Modeling Mode Tools are continually calling AppendChange() as the user interacts with the Tool, and the Gizmos do this as well. So, we can build a basic Undo/Redo History system simply by storing these Changes in the order they come in, and then stepping back/forward in the list on Undo/Redo, calling Revert()/Apply() on each FToolCommandChange object.

BeginUndoTransaction() and EndUndoTransaction() are related functions that mark the start and end of a set of Change records that should be grouped - generally AppendChange() will be called one or more times in-between. To provide the correct UX - ie that a single Undo/Redo hotkey/command processes all the Changes at once - the ToolsFrameworkDemo has a very rudimentary system that stores a set of FCommandChanges.

IToolsContextRenderAPI

This API is passed to UInteractiveTool::Render() and UInteractiveGizmo::Render() to provide information necessary for common rendering tasks. GetPrimitiveDrawInterface() returns an implementation of the abstract FPrimitiveDrawInterface API, which is a standard UE interface that provides line and point drawing functions (commonly abbreviated as PDI). Various Tools use the PDI to draw basic line feedback, for example the edges of the currently Polygon being drawn in the Draw Polygon Tool. Note, however, that PDI line drawing at Runtime is not the same as PDI line drawing in the Editor - it has lower quality and cannot draw the stipped-when-hidden lines that the Editor can.

GetCameraState(), GetSceneView(), and GetViewInteractionState() return information about the current View. These are important in the Editor because the user may have multiple 3D viewports visible (eg in 4-up view), and the Tool must draw correctly in each. At Runtime, there is generally a single camera/view and you should be fine with the basic implementations in the ToolsFramworkDemo. However if you wanted to implement multiple views, you would need to provide them correctly in this API.

class IToolsContextRenderAPI
{
    FPrimitiveDrawInterface* GetPrimitiveDrawInterface();
    FViewCameraState GetCameraState();
    const FSceneView* GetSceneView();
    EViewInteractionState GetViewInteractionState();
}

IToolsContextAssetAPI

The ITooslContextAssetAPI can be used to emit new objects. This is an optional API, and I have only listed the top-level function below, there are other functions that the API includes that are somewhat specific to the UE Editor. This is the hardest part to abstract as it requires some inherent assumptions about what “Objects” are. However, it is also not something that you are required to use in your own Tools. The GenerateStaticMeshActor() function is used by the Editor Modeling Tools to spawn new Static Mesh Assets/Components/Actors, for example in the Draw Polygon Tool, this function is called with the extruded polygon (part of the AssetConfig argument) to create the Asset. This creation process involves things like finding a location (which possibly spawns dialog boxes/etc), creating a new package, and so on.

class IToolsContextAssetAPI
{
    AActor* GenerateStaticMeshActor(
        UWorld* TargetWorld,
        FTransform Transform,
        FString ObjectBaseName,
        FGeneratedStaticMeshAssetConfig&& AssetConfig);
 }

At Runtime, you cannot create Assets, so this function has to do “something else”. In the ToolsFrameworkDemo, I have implemented GenerateStaticMeshActor(), so that some Modeling Mode Tools like the Draw Polygon Tool are able to function. However, it emits a different Actor type entirely.

Actor/Component Selections and PrimitiveComponentTargets

FPrimitiveComponentTarget was removed in UE5, and replaced with a new approach/system. See the section entitled UToolTargets in my article about UE5 changes to the Interactive Tools Framework: https://www.gradientspace.com/tutorials/2022/6/1/the-interactive-tools-framework-in-ue5

In the Tools and ToolBuilders Section above, I described FToolBuilderState, and how the ToolManager constructs a list of selected Actors and Components to pass to the ToolBuilder. If your Tool should act on Actors or Components, you can pass that selection on to the new Tool instance. However if you browse the Modeling Mode Tools code, you will see that most tools act on something called a FPrimitiveComponentTarget, which is created in the ToolBuilders based on the selected UPrimitiveComponents. And we have base classes USingleSelectionTool and UMultiSelectionTool, which most Modeling Mode tools derive from, that hold these selections.

This is not something you need to do if you are building your own Tools from scratch. But, if you want to leverage Modeling Mode Tools, you will need to understand it, so I will explain. The purpose of FPrimitiveComponentTarget is to provide an abstraction of “a mesh that can be edited” to the Tools. This is useful because we have many different Mesh types in Unreal (and you may have your own). There is FMeshDescription (used by UStaticMesh), USkeletalMesh, FRawMesh, Cloth Meshes, Geometry Collections (which are meshes), and so on. Mesh Editing Tools that have to manipulate low-level mesh data structures would essentially require many parallel code paths to support each of these. In addition, updating a mesh in Unreal is expensive. As I have explained in previous tutorials, when you modify the FMeshDescription inside a UStaticMesh, a “build” step is necessary to regenerate rendering data, which can take several seconds on large meshes. This would not be acceptable in, for example, a 3D sculpting Tool where the user expects instantaneous feedback.

So, generally the Modeling Mode Tools cannot directly edit any of the UE Component mesh formats listed above. Instead, the ToolBuilder wraps the target Component in a FPrimitiveComponentTarget implementation, which must provide an API to Read and Write it’s internal mesh (whatever the format) as a FMeshDescription. This allows Tools that want to edit meshes to support a single standard input/output format, at the (potential) cost of mesh conversions. In most Modeling Mode Tools, we then convert that FMeshDescription to a FDynamicMesh3 for actual editing, and create a new USimpleDynamicMeshComponent for fast previews, and only write back the updated FMeshDescription on Tool Accept. But this is encapsulated inside the Tool, and not really related to the FPrimtiveComponentTarget.

FComponentTargetFactory

We need to allow the Interactive Tools Framework to create an FPrimitiveComponentTarget-subclass wrapper for a Component it does not know about (as many Components are part of plugins not visible to the ITF). For example, UProceduralMeshComponent or USimpleDynamicMeshComponent. To do this we provide a FComponentTargetFactory implementation, which has two functions:

class INTERACTIVETOOLSFRAMEWORK_API FComponentTargetFactory
{
public:
    virtual bool CanBuild( UActorComponent* Candidate ) = 0;
    virtual TUniquePtr<FPrimitiveComponentTarget> Build( UPrimitiveComponent* PrimitiveComponent ) = 0;
};

These are generally very simple, for an example, see FStaticMeshComponentTargetFactory in EditorComponentSourceFactory.cpp, which builds FStaticMeshComponentTarget instances for UStaticMeshComponents. The FStaticMeshComponentTarget is also straightforward in this case. We will take advantage of this API to work around some issues with Runtime usage below.

Finally once the FComponentTargetFactory is available, the global function AddComponentTargetFactory() is used to register it. Unfortunately, in UE4.26 this function stores the Factory in a global static TArray that is private to ComponentSourceInterfaces.cpp, and as a result cannot be modified or manipulated in any way. On Startup, the Editor will register the default FStaticMeshComponentTargetFactory and also FProceduralMeshComponentTargetFactory, which handles PMCs. Both of these factories have issues that prevent them from being used at Runtime for mesh editing Tools, and as a result, until this system is improved, we cannot use SMCs or PMCs for Runtime mesh editing. We will instead create a new ComponentTarget for USimpleDynamicMeshComponent (see previous tutorials for details on this mesh Component type).

ToolBuilderUtil.h

If you look at the ToolBuilders for most tools, you will see that the CanBuildTool() and BuildTool() implementations are generally calling static functions in the ToolBuilderUtil namespace, as well as the functions CanMakeComponentTarget() and MakeComponentTarget(). These latter two functions enumerate through the list of registered ComponentTargetFactory instances to determine if a particular UPrimitiveComponent type can be handled by any Factory. The ToolBuilderUtil functions are largely just iterating through selected Components in the FToolBuilderState (described above) and calling a lambda predicate (usually one of the above functions).

I will re-iterate here that you are not required to use the FPrimitiveComponentTarget system in your own Tools, or even the FToolBuilderState. You could just as easily query some other (global) Selection system in your ToolBuilders, check for casts to your target Component type(s), and pass UPrimitiveComponent* or subclasses to your Tools. However, as I mentioned, the Modeling Mode tools work this way, and it will be a significant driver of the design of the Runtime mesh editing Tools Framework I will now describe.

Runtime Tools Framework Back-End

Creating a Runtime back-end for the Interactive Tools Framework is not really that complicated. The main things we have to figure out are:

1. How to collect mouse input events (ie mouse down/move/up) and send this data to the UInputRouter

2. How to implement the IToolsContextQueriesAPI and IToolsContextRenderAPI

3. (Optionally) how to implement IToolsContextTransactionsAPI and IToolsContextAssetAPI

4. How/when to Render() and Tick() the UInteractiveToolManager and UInteractiveGizmoManager

That’s it. Once these things are done (even skipping step 3) then basic Tools and Gizmos (and even the UTransformGizmo) will be functional.

In this sample project, all the relevant code to accomplish the above is in the RuntimeToolsSystem module, split into four subdirectories:

• RuntimeToolsFramework\ - contains the core ToolsFramework implementation

• MeshScene\ - a simple “Scene Graph” of Mesh Objects, which is what our mesh editing Tools will edit, and a basic History (ie undo/redo) system

• Interaction\ - basic user-interface interactions for object selection and transforming with a UTransformGizmo, built on top of the ITF

• Tools\ - subclasses of several MeshModelingToolset UInteractiveTools and/or Builders, necessary to allow them to function properly at Runtime

At a high level, here is how everything is connected, in plain english (hopefully this will make it easier to follow the descriptions below). A custom Game Mode, AToolsFrameworkDemoGameModeBase, is initialized on Play, and this in turn initializes the URuntimeToolsFrameworkSubsystem, which manages the Tools Framework, and the URuntimeMeshSceneSubsystem. The latter manages a set of URuntimeMeshSceneObject’s, which are wrappers around a mesh Actor and Component that can be selected via clicking and transformed with a UTransformGizmo. The URuntimeToolsFrameworkSubsystem initializes and owns the UInteractiveToolsContext, as well as various helper classes like the USceneObjectSelectionInteraction (which implements clicking selection), the USceneObjectTransformInteraction (which manages the transform Gizmo state), and the USceneHistoryManager (which provides the undo/redo system). The URuntimeToolsFrameworkSubsystem also creates a UToolsContextRenderComponent, which is used to allow PDI rendering in the Tools and Gizmos. Internally, the URuntimeToolsFrameworkSubsystem also defines the various API implementations, this is all fully contained in the cpp file. The final piece is the default Pawn for the Game Mode, which is a AToolsContextActor that is spawned by the GameMode on Play. This Actor listens for various input events and forwards them to the URuntimeToolsFrameworkSubsystem. A FSimpleDynamicMeshComponentTargetFactory is also registered on Play, which allows for the Mesh Component used in the URuntimeMeshSceneObject to be edited by existing Modeling Mode tools.

Whew! Since it’s relatively independent from the Tools Framework aspects, lets start with the Mesh Scene aspects.

URuntimeMeshSceneSubsystem and MeshSceneObjects

The purpose of this demo is to show selection and editing of meshes at Runtime, via the ITF. Conceivably this could be done such that any StaticMeshActor/Component could be edited, similar to how Modeling Mode works in the UE Editor. However, as I have recommended in previous tutorials, if you are building some kind of Modeling Tool app, or game Level Editor, I don’t think you want to build everything directly out of Actors and Components. At minimum, you will likely want a way to serialize your “Scene”. And you might want to have visible meshes in your environment that are not editable (if even just as 3D UI elements). I think it’s useful to have an independent datamodel that represents the editable world - a “Scene” of “Objects” that is not tied to particular Actors or Components. Instead, the Actors/Components are a way to implement desired functionality of these SceneObjects, that works in Unreal Engine.

So, that is what I’ve done in this demo. URuntimeMeshSceneObject is a SceneObject that is represented in the UE level by a ADynamicSDMCActor, which I described in previous tutorials. This Actor is part of the RuntimeGeometryUtils plugin. It spawns/manages a child mesh USimpleDynamicMeshComponent that can be updated when needed. In this project we will not be using any of the Blueprint editing functionality I previously developed, instead we will use the Tools to do the editing, and only use the SDMC as a way to display our source mesh.

URuntimeMeshSceneSubsystem manages the set of existing URuntimeMeshSceneObjects, which I will abbreviate here (and in the code) as an “SO”. Functions are provided to spawn a new SO, find one by Actor, delete one or many SOs, and also manage a set of selected SOs. In addition, the FindNearestHitObject() can be used to cast rays into the Scene, similar to a LineTrace (but will only hit the SOs).

The URuntimeMeshSceneSubsystem also owns the Materials assigned to the SO when selected, and the default Material. There is only baseline support for Materials in this demo, all created SOs are assigned the DefaultMaterial (white), and when selected are swapped to the SelectedMaterial (orange). However the SOs do track an assigned material and so you could relatively easily extend what is there now.

USceneHistoryManager

Changes to the Scene - SceneObject creation, deletion, and editing, Selection changes, Transform changes, and so on - are stored by the USceneHistoryManager. This class stores a list of FChangeHistoryTransaction structs, which store sequences of FChangeHistoryRecord, which is a tuple (UObject*, FCommandChange, Text). This system roughly approximates the UE Editor transaction system, however only explicit FCommandChange objects are supported, while in the Editor, changes to UObjects can be automatically stored in a transaction. I described FCommandChange in more detail above, in the IToolsContextTransactionsAPI section. Essentially these are objects that have Apply() and Revert() functions, which must “redo” or “undo” their effect on any modified global state.

The usage pattern here is to call BeginTransaction(), then AppendChange() one or more times, then EndTransaction(). The IToolsContextTransactionsAPI implementation will do this for ITF components, and things like the scene selection change will do it directly. The Undo() function rolls back to the previous history state/transaction, and the Redo() function rolls forward. Generally the idea is that all changes are grouped into a single transaction for a single high-level user “action”, so that one does not have to Undo/Redo multiple times to get “through” a complex state change. To simplify this, BeginTransaction()/EndTransaction() calls can be nested, this occurs frequently when multiple separate functions need to be called and each needs to emit it’s own transactions. Like any app that supports Undo/Redo, the History sequence is truncated if the user does Undo one or more times, and then does an action that pushes a new transaction/change.

AToolsContextActor

View fullsize

In an Unreal Engine game, the player controls a Pawn Actor, and in a first-person-view game the scene is rendered from the Pawn’s viewpoint. In the ToolsFrameworkDemo we will implement a custom ADefaultPawn subclass called AToolsContextActor to collect and forward user input to the ITF. In addition, this Actor will handle various hotkey input events defined in the Project Settings. And finally, the AToolsContextActor is where I have implemented standard right-mouse-fly (which is ADefaultPawn’s standard behavior, I am just forwarding calls to it) and the initial steps of Maya-style alt-mouse camera control (however orbit around a target point is not implemented, yet).

All the event connection setup is done in AToolsContextActor::SetupPlayerInputComponent(). This is a mix of hotkey events defined in the Input section of the Project Settings, and hardcoded button Action and mouse Axis mappings. Most of the hardcoded mappings - identifiable as calls to UPlayerInput::AddEngineDefinedActionMapping() - could be replaced with configurable mappings in the Project Settings.

This Actor is automatically created by the Game Mode on startup. I will describe this further below.

I will just mention here that another option, rather than having the Pawn forward input to the ITF’s InputRouter, would be to use a custom ViewportClient. The ViewportClient is “above” the level of Actors and Pawns, and to some degree is responsible for turning raw device input into the Action and Axis Mappings. Since our main goal as far as the ITF is concerned is simply to collect device input and forward it to the ITF, a custom ViewportClient might be a more natural place to do that. However, that’s just not how I did it in this demo.

URuntimeToolsFrameworkSubsystem

The central piece of the Runtime ITF back-end is the URuntimeToolsFrameworkSubsystem. This UGameInstanceSubsystem (essentially a Singleton) creates and initializes the UInteractiveToolsContext, all the necessary IToolsContextAPI implementations, the USceneHistoryManager, and the Selection and Transform Interactions, as well as several other helper objects that will be described below. This all occurs in the ::InitializeToolsContext() function.

The Subsystem also has various Blueprint functions for launching Tools and managing the active Tool. These are necessary because the ITF is not currently exposed to Blueprints. And finally it does a bit of mouse state tracking, and in the ::Tick() function, constructs a world-space ray for the cursor position (which is a bit of relatively obscure code) and then forwards this information to the UInputRouter, as well as Tick’ing and Render’ing the ToolManager and GizmoManager.

If this feels like a bit of a grab-bag of functionality, well, it is. The URuntimeToolsFrameworkSubsystem is basically the “glue” between the ITF and our “Editor”, which in this case is extremely minimal. The only other code of note are the various API implementations, which are all defined in the .cpp file as they are not public classes.

FRuntimeToolsContextQueriesImpl is the implementation of the IToolsContextQueriesAPI. This API provides the SelectionState to ToolBuilders, as well as supporting a query for the current View State and Coordinate System state (details below). The ExecuteSceneSnapQuery() function is not implemented and just returns false. However, if you wanted to support optional Transform Gizmo features like grid snapping, or snapping to other geometry, this would be the place to start.

FRuntimeToolsContextTransactionImpl is the implementation of the IToolsContextTransactionsAPI. Here we just forward the calls directly to the USceneHistoryManager. Currently I have not implemented RequestSelectionChange(), which some Modeling Mode Tools use to change the selection to newly-created objects, and also ignored PostInvalidation() calls, which are used in the UE Editor to force a viewport refresh in non-Realtime mode. Built games always run in Realtime, so this is not necessary in a standard game, but if you are building an app that does not require constant 60fps redraws, and have implemented a scheme to avoid repaints, this call can provide you with a cue to force a repaint to see live Tool updates/etc.

FRuntimeToolsFrameworkRenderImpl is the implementation of the IToolsContextRenderAPI. The main purpose of this API is to provide a FPrimitiveDrawInterface implementation to the Tools and Gizmos. This is one of the most problematic parts of using the Modeling Mode Tools at Runtime, and I will describe how this is implemented in the section below on the UToolsContextRenderComponent. Otherwise, functions here just forward information provided by the RuntimeToolsFrameworkSubsystem.

Finally FRuntimeToolsContextAssetImpl implements IToolsContextAssetAPI, which in our Runtime case is very limited. Many of the functions in this API are intended for more complex Editor usage, because the UE Editor has to deal with UPackages and Assets inside them, can do things like pop up internal asset-creation dialogs, has a complex system for game asset paths, and so on. Several of the functions in this API should perhaps not be part of the base API, as Tools do not call them directly, but rather call utility code that uses these functions. As a result we only need to implement the GenerateStaticMeshActor() function, which Tools do call, to emit new objects (for example the DrawPolygon Tool, which draws and extrudes a new mesh). The function name is clearly not appropriate because we don’t want to emit a new AStaticMeshActor, but rather a new URuntimeMeshSceneObject. Luckily, in many Modeling Mode Tools, the returned AActor type is not used - more on this below.

And that’s it! When I mentioned the “ITF Back-End” or “Editor-Like Functionality”, this is all I was referring to. 800-ish lines of extremely verbose C++, most of it relatively straightforward “glue” between different systems. Even quite a few of the existing pieces are not necessary for a basic ITF implementation, for example if you didn’t want to use the Modeling Mode Tools, you don’t need the IToolsContextAssetAPI implementation at all.

USceneObjectSelectionInteraction and USceneObjectTransformInteraction

When I introduced the ITF, I focused on Tools and Gizmos as the top-level “parts” of the ITF, ie the sanctioned methods to implement structured handling of user input (via InputBehaviors), apply actions to objects, and so on. However, there is no strict reason to use either Tools or Gizmos to implement all user interactions. To demonstrate this I have implemented the “click-to-select-SceneObjects” interaction as a standalone class USceneObjectSelectionInteraction.

USceneObjectSelectionInteraction subclasses IInputBehaviorSource, so it can be registered with the UInputRouter, and then it’s UInputBehaviors will be automatically collected and allowed to capture mouse input. A USingleClickInputBehavior is implemented which collects left-mouse clicks, and supports Shift+Click and Ctrl+Click modifier keys, to add to the selection, or toggle selection. The IClickBehaviorTarget implementation functions just determine what state the action should indicate, and apply them to the scene via the URuntimeMeshSceneSubsystem API functions. As a result, the entire click-to-select Interaction requires a relatively tiny amount of code. If you wanted to implement additional selection interactions, like a box-marquee select, this could be relatively easy done by switching to a UClickDragBehavior/Target and determining if the user has done a click vs drag via a mouse-movement threshold.

The URuntimeToolsFrameworkSubsystem simply creates an instance of this class on startup, registers it with the UInputRouter, and that’s all the rest of the system knows about it. It is of course possible to implement selection as a Tool, although generally selection is a “default” mode, and switching out-of/into a default Tool when any other Tool starts of exits requires a bit of care. Alternately it could be done with a Gizmo that has no in-scene representation, and is just always available when selection changes are supported. This would probably be my preference, as a Gizmo gets Tick() and Render() calls and that might be useful (for example a marquee rectangle could be drawn by Render()).

As the selection state changes, a 3D Transform Gizmo is continually updated - either it moves between the origin of the selected object, to the shared origin if there are multiple selected objects, or disappears if no object is selected. This behavior is implemented in USceneObjectTransformInteraction, which is similarly created by the URuntimeToolsFrameworkSubsystem. A delegate of URuntimeMeshSceneSubsystem, OnSelectionModified, is used to kick off updates as the scene selection is modified. The UTransformGizmo that is spawned acts on a UTransformProxy, which is given the current selection set. Note that any selection change results in a new UTransformGizmo being spawned, and the existing one destroyed. This is a bit heavy, and it is possible to optimize this to re-use a single Gizmo (various Modeling Mode Tools do just that).

One last note is the management of the active Coordinate System. This is handled largely under the hood, the UTransformGizmo will query the available IToolsContextQueriesAPI to determine World or Local coordinate frames. This could be hardcoded, but to support both, we need somewhere to put this bit of state. Currently I have placed it in the URuntimeToolsFrameworkSubsystem, with some BP functions exposed to allow the UI to toggle the option.

UToolsContextRenderComponent

I mentioned above that the IToolsContextRenderAPI implementation, which needs to return a FPrimitiveDrawInterface (or “PDI”) that can be used to draw lines and points, is a bit problematic. This is because in the UE Editor, the Editor Mode that hosts the ITF has it’s own PDI that can simply be passed to the Tools and Gizmos. However at Runtime, this does not exist, the only place we can get access to a PDI implementation is inside the rendering code for a UPrimitiveComponent, which runs on the rendering thread (yikes!).

If that didn’t entirely make sense, essentially what you need to understand is that we can’t just “render” from anywhere in our C++ code. We can only render “inside” a Component, like a UStaticMeshComponent or UProceduralMeshComponent. But, our Tools and Gizmos have ::Render() functions that run on the Game Thread, and are very far away from any Components.

So, what I have done is make a custom Component, called UToolsContextRenderComponent, that can act as a bridge. This Component has a function ::GetPDIForView(), which returns a custom FPrimitiveDrawInterface implementation (FToolsContextRenderComponentPDI to be precise, although this is hidden inside the Component). The URuntimeToolsFrameworkSubsystem creates an instance of this PDI every frame to pass to the Tools and Gizmos. The PDI DrawLine() and DrawPoint() implementations, rather than attempting to immediately render, store each function call’s arguments in a list. The Components SceneProxy then takes these Line and Point parameter sets and passes them on the standard UPrimitiveComponent PDI inside FToolsContextRenderComponentSceneProxy::GetDynamicMeshElements() implementation (which is called by the renderer to get per-frame dynamic geometry to draw).

This system is functional, and allows the Modeling Mode Tools to generally work as they do in the Editor. However one hitch is that the Game and Render threads run in parallel. So, if nothing is done, we can end up with GetDynamicMeshElements() being called before the Tools and Gizmos have finished drawing, and this causes flickering. Currently I have “fixed” this by calling FlushRenderingCommands() at the end of URuntimeToolsFrameworkSubsystem::Tick(), which forces the render thread to process all the outstanding submitted geometry. However, this may not fully resolve the problem.

One other complication is that in the UE Editor, the PDI line and point drawing can draw “hidden lines”, ie lines behind front-facing geometry, with a stipple pattern. This involves using Custom Depth/Stencil rendering in combination with a Postprocess pass. This also does not exist at Runtime. However, in your own application, you actually have more ability to do these kinds of effects, because you are fully in control of these rendering systems, while in the Editor, they need to be added “on top” of any in-game effects and so are necessarily more limited. This article gives a good overview of how to implement hidden-object rendering, as well as object outlines similar to the UE Editor.

FSimpleDynamicMeshComponentTarget

As I described above in the section on PrimitiveComponentTargets, to allow the mesh editing tools from Modeling Mode to be used in this demo, we need to provide a sort of “wrapper” around the UPrimitiveComponents we want to edit. In this case that will be USimpleDynamicMeshComponent. The code for FSimpleDynamicMeshComponentTarget, and it’s associated Factory, is relatively straightforward. You might notice, if you dive in, that the FDynamicMesh3 in the SDMC is being converted to a FMeshDescription to pass to the Tools, which then convert it back to a FDynamicMesh3 for editing. This is a limitation of the current design, which was focused on Static Meshes. If you are building your own mesh editing Tools, this conversion would not be necessary, but to use the Modeling Mode toolset, it is unavoidable.

Note that changes to the meshes (stored in ::CommitMesh()) are saved in the change history as FMeshReplacementChange, which stores two full mesh copies. This is not ideal for large meshes, however the mesh “deltas” that the modeling tools create internally to store changes on their preview meshes (eg in 3D sculpting) do not currently “bubble up”.

Finally, I will just re-iterate that because of the issues with Factory registration described in the section on FPrimitiveComponentTarget, it is not possible to directly edit UStaticMeshComponent or UProceduralMeshComponent at Runtime in UE4.26, with the Modeling Mode toolset. Although, since it’s largely only the ToolBuilders that use the FPrimitiveComponentTargetFactory registry, you might be able to get them to work with custom ToolBuilders that directly create alternate FPrimitiveComponentTarget implementations. This is not a route I have explored.

AToolsFrameworkDemoGameModeBase

The final C++ code component of the tutorial project is AToolsFrameworkDemoGameModeBase. This is a subclass of AGameModeBase, which we will configure in the Editor to be used as the default game mode. Essentially, this is what “launches” our Runtime Tools Framework. Note that this is not part of the RuntimeToolsFramework module, but rather the base game module, and there is no need for you to initialize things this way in your own app. For example, if you wanted to implement some kind of in-game level design/editing Tools, you would likely fold this code into your existing Game Mode (or perhaps launch a new one on demand). You also don’t need to use a Game Mode to do this, although a complication in that case is the default pawn AToolsContextActor, which might need to be replaced too.

Very little happens in this Game Mode. We configure it to Tick, and in the Tick() function, we Tick() the URuntimeToolsFrameworkSubsystem. Otherwise all the action is in AToolsFrameworkDemoGameModeBase::InitializeToolsSystem(), where we initialize the URuntimeMeshSceneSubsystem and URuntimeToolsFrameworkSubsystem, and then register the set of available Tools with the ToolManager. All this code could (and perhaps should) be moved out of the Game Mode itself, and into some utility functions.

ToolsFrameworkDemo Project Setup

If you are planning to set up your own Project based on this tutorial, or make changes, there are various assets involved, and Project Settings, that you need to be aware of. The Content Browser screenshot below shows the main Assets. DefaultMap is the level I have used, this simply contains the ground plane and initializes the UMG User Interface in the Level Blueprint (see below).

BP_ToolsContextActor is a Blueprint subclass of AToolsContextActor, which is configured as the Default Pawn in the Game Mode. In this BP Actor I have disabled the Add Default Movement Bindings setting, as I set up those bindings manually in the Actor. DemoPlayerController is a Blueprint subclass of AToolsFrameworkDemoPlayerController, again this exists just to configure a few settings in the BP, specifically I enabled Show Mouse Cursor so that the standard Windows cursor is drawn (which is what one might expect in a 3D Tool) and disabled Touch Events. Finally DemoGameMode is a BP subclass of our AToolsFrameworkDemoGameModeBase C++ class, here is where we configure the Game Mode to spawn our DemoPlayerController and BP_ToolsContextActor instead of the defaults.

BP_ToolsContextActor Settings

DemoPlayerController Settings

DemoGameMode Settings

Finally in the Project Settings dialog, I configured the Default GameMode to be our DemoGameMode Blueprint, and DefaultMap to the the Editor and Game startup map. I also added various actions in the Input section, I showed a screenshot of these settings above, in the description of AToolsContextActor. And finally in the Packaging section, I added two paths to Materials to the Additional Asset Directories to Cook section. This is necessary to force these Materials to be included in the built Game executable, because they are not specifically referenced by any Assets in the Level.

View fullsize

Packaging settings - these force Material assets to be included in the built game

RuntimeGeometryUtils Updates

In my previous tutorials, I have been accumulating various Runtime mesh generation functionality in the RuntimeGeometryUtils plugin. To implement this tutorial, I have made one significant addition, URuntimeDynamicMeshComponent. This is a subclass of USimpleDynamicMeshComponent (SDMC) that adds support for collision and physics. If you recall from previous tutorials, USimpleDynamicMeshComponent is used by the Modeling Mode tools to support live previews of meshes during editing. In this context, SDMC is optimized for fast updates over raw render performance, and since it is only used for “previews”, does not need support for collision or physics.

However, we have also been using SDMC as a way to render runtime-generated geometry. In many ways it is very similar to UProceduralMeshComponent (PMC), in that respect, however one significant advantage of PMC was that it supported collision geometry, which mean that it worked properly with the UE raycast/linetrace system, and with the Physics/Collision system. It turns out that supporting this is relatively straightforward, so I created the URuntimeDynamicMeshComponent subclass. This variant of SDMC, I guess we can call it RDMC, supports simple and complex collision, and a function SetSimpleCollisionGeometry() is available which can take arbitrary simple collision geometry (which even PMC does not support). Note, however, that currently Async physics cooking is not supported. This would not be a major thing to add, but I haven’t done it.

I have switched the Component type in ADynamicSDMCActor to this new Component, since the functionality is otherwise identical, but now the Collision options on the base Actor work the same way they do on the PMC variant. The net result is that previous tutorial demos, like the bunny gun and procedural world, should work with SDMC as well as PMC. This will open the door for more interesting (or performant) runtime procedural mesh tools in the future.

Using ModelingMode Tools at Runtime

It’s taken quite a bit of time, but we are now at the point where we can expose existing mesh editing Tools in the MeshModelingToolset in our Runtime game, and use them to edit selected URuntimeMeshSceneObject’s. Conceptually, this “just works” and adding the basic ability for a Tool to work only requires registering a ToolBuilder in AToolsFrameworkDemoGameModeBase::RegisterTools(), and then adding some way (hotkey, UMG button, etc) to launch it via the URuntimeToolsFrameworkSubsystem::BeginToolByName(). This works for many Tools, for example PlaneCutTool and EditMeshPolygonsTool worked out-of-the-box.

However, not all Tools are immediately functional. Similar to the global ToolTargetTargetFactory system, various small design decisions that likely seemed insignificant at the time can prevent a Tool from working in a built game. Generally, with a bit of experimentation it is possible to work around these problems with a small amount of code in a subclass of the base Tool. I have done this in several cases, and I will explain these so that if you try to expose other Tools, you might have a strategy for what to try to do. If you find yourself stuck, please post in the Comments with information about the Tool that is not working, and I will try to help.

Note that to make a Tool subclass, you will also need to make a new ToolBuilder that launches that subclass. Generally this means subclassing the base Builder and overriding a function that creates the Tool, either the base ::BuildTool() or a function of the base Builder that calls NewObject<T> (those are usually easier to deal with).

In several cases, default Tool Settings are problematic. For example the URemeshTool by default enables a Wireframe rendering that is Editor-Only. So, it is necessary to override the Setup() function, call the base Setup(), and then disable this flag (There is unfortunately no way to do this in the Builder currently, as the Builder does not get a chance to touch the Tool after it allocates a new instance).

Tools that create new objects, like UDrawPolygonTool, generally do not work at Runtime without modification. In many cases the code that emits the new object is #ifdef’d out, and a check() is hit instead. However we can subclass these Tools and replace either the Shutdown() function, or an internal function of the Tool, to implement the new-object creation (generally from a FDynamicMesh3 the Tool generated). URuntimeDrawPolygonTool::EmitCurrentPolygon() is an example of doing this for the UDrawPolygonTool, and URuntimeMeshBooleanTool::Shutdown() for the UCSGMeshesTool. In the latter case, the override performs a subset of the base Tool code, as I only supported replacing the first selected Input object.

These are the two main issues I encountered. A third complication is that many of the existing Tools, particularly older Tools, do not use the WatchProperty() system to detect when values of their UInteractiveToolPropertySet settings objects have been modified. Instead of polling, they depend on Editor-only callbacks, which do not occur in a built game. So, if you programmatically change settings of these PropertSets, the Tool will not update to reflect their values without a nudge. However, I have coupled those “nudges” with a way to expose Tool Settings to Blueprints, which I will now explain.

Blueprint-Exposed ToolPropertySets

One major limitation of the Tools Framework in 4.26 is that although it is built out of UObjects, none of them are exposed to Blueprints. So, you cannot easily do a trivial thing like hook up a UMG UI to the active Tool, to directly change Tool Settings. However if we subclass an existing Tool, we can mark the subclass as a UCLASS(BlueprintType), and then cast the active Tool (accessed via URuntimeToolsFrameworkSubsystem::GetActiveTool()) to that type. Similarly we can define a new UInteractiveToolPropertySet, that is also UCLASS(BlueprintType), and expose new UProperties marked BlueprintReadWrite to make them accessible from BP.

To include this new Property Set, we will then subclass the Tool ::Setup() function, call the base-class ::Setup(), and then create and register our new PropertySet. For each property we will add a WatchProperty() call that forwards changes from our new PropertySet to the base tool Settings, and then if necessary call a function to kick off a recomputation or update (for example URuntimeMeshBooleanTool will have to call Preview->InvalidateResult()).

One complication is enum-valued Settings, which in the Editor will automatically generate dropdown lists, but this is not possible with UMG. So, in those cases I used integer UProperties and mapped integers to enums myself. So, for example, here is all the PropertySet-related code for the URuntimeDrawPolygonTool of UDrawPolygonTool (I have omitted the EmitCurrentPolygon() override and new ToolBuilder that I mentioned above). This is a cut-and-paste pattern that I was able to re-use in all my Tool overrides to expose Tool Properties for my UMG UI.

UENUM(BlueprintType)
enum class ERuntimeDrawPolygonType : uint8
{
    Freehand = 0, Circle = 1, Square = 2, Rectangle = 3, RoundedRectangle = 4, HoleyCircle = 5
};

UCLASS(BlueprintType)
class RUNTIMETOOLSSYSTEM_API URuntimeDrawPolygonToolProperties : public UInteractiveToolPropertySet
{
    GENERATED_BODY()
public:
    UPROPERTY(BlueprintReadWrite)
    int SelectedPolygonType;
};

UCLASS(BlueprintType)
class RUNTIMETOOLSSYSTEM_API URuntimeDrawPolygonTool : public UDrawPolygonTool
{
    GENERATED_BODY()
public:
    virtual void Setup() override;

    UPROPERTY(BlueprintReadOnly)
    URuntimeDrawPolygonToolProperties* RuntimeProperties;
};

void URuntimeDrawPolygonTool::Setup()
{
    UDrawPolygonTool::Setup();

    // mirror properties we want to expose at runtime 
    RuntimeProperties = NewObject<URuntimeDrawPolygonToolProperties>(this);
    RuntimeProperties->SelectedPolygonType = (int)PolygonProperties->PolygonType;
    RuntimeProperties->WatchProperty(RuntimeProperties->SelectedPolygonType,
        [this](int NewType) { PolygonProperties->PolygonType = (EDrawPolygonDrawMode)NewType; });

    AddToolPropertySource(RuntimeProperties);
}

ToolPropertySet Keepalive Hack

One major hitch I ran into in trying to get the MeshModelingToolset Tools to work in a built game is that it turns out that they do something…illegal…with UObjects. This really gets into the weeds, but I’ll explain it briefly in case it is relevant to you. I previously mentioned that UInteractiveToolPropertySet is used to expose “Tool Settings” in a structured way in nearly all the Tools. One desirable property of a system like this is to be able to save the state of Settings between Tool invocations. To do this, we can just hold on to an instance of the Property Set itself, but we need to hold it somewhere.

Various Editor systems do this by holding a pointer to the saved settings UObject in the CDO of some other UObject - each UObject has a CDO (Class Default Object) which is like a “template” used to construct additional instances. CDOs are global and so this is a handy place to put things. However, in the Editor the CDO will keep this UObject from being Garbage Collected (GC’d), but at Runtime, it will not! And in fact at Runtime, the Garbage Collector does a safety check to determine that this has not been done, and if it detects this, kills the game (!). This will need to be fixed in future versions of UE, but for this demo to function in a binary 4.26 build, we will need a workaround.

First, I had to disable the GC safety check by setting the global GShouldVerifyGCAssumptions = false in URuntimeToolsFrameworkSubsystem::InitializeToolsContext(). This prevents the hard kill, but the saved PropertySets will still be Garbage-Collected and result in crashes later, when the Tool tries to access them and assumes they still exist. So, in the URuntimeToolsFrameworkSubsystem::OnToolStarted() event handler, the AddAllPropertySetKeepalives() function is called, which iterates through the CDOs of all the registered PropertySet UObjects of the new Tool, and adds these “saved settings” UObjects to a TArray that will prevent them from being GC’d.

This is…a gross hack. But fully functional and does not appear to have any problematic side-effects. But I intend to resolve the underlying architectural issues in the future.

User Interface

The point of this tutorial was to demonstrate at-runtime usage of the Interactive Tools Framework and Mesh Modeling Toolset, not to actually build a functional runtime modeling tool. However, to actually be able to launch and use the Tools for the demo, I had to build a minimal UMG user interface. I am not an expert with UMG (this is the first time I’ve used it) so this might not be the best way to do it. But, it works. In the /ToolUI subfolder, you will find several UI widget assets.

ToolTestUI is the main user interface, which lives in the upper-left corner, there is an image below-right. I described the various Tool buttons at the start of the Tutorial. The Accept, Cancel, and Complete buttons dynamically update visibility and enabled-ness, based on the active Tool state, this logic is in the Blueprint. Undo and Redo do what you expect, and the World button toggles between World and Local frames for any active Gizmos. This UI is spawned on BeginPlay by the Level Blueprint, below-right.

View fullsize

There are also several per-tool UI panels that expose Tool settings. These per-Tool UI panels are spawned by the ToolUI buttons after they launch the Tool, see the ToolUI Blueprint, it’s very straightforward. I have only added these settings panels for a few of the Tools, and only exposed a few settings. It’s not really much work to add settings, but it is a bit tedious, and since this is a tutorial I wasn’t too concerned with exposing all the possible options. The screenshots below are from the DrawPolygonToolUI, showing the in-game panel (left) and the UI Blueprint (right). Essentially, on initialization, the Active Tool is cast to the correct type and we extract the RuntimeProperties property set, and then initialize all the UI widgets (only one in this case). Then on widget event updates, we forward the new value to the property set. No rocket science involved.

sincere Apologies for the terrible UI layout and sizing.

View fullsize

Final Notes

I have had many people ask about whether the UE Editor Modeling Mode Tools and Gizmos could be used at Runtime, and my answer has always been “well, it’s complicated, but possible”. I hope this sample project and write-up answers the question! It’s definitely possible, and between the GeometryProcessing library and MeshModelingToolset tools and components, there is an enormous amount of functionality available in UE4.26 that can be used to build interactive 3D content creation apps, from basic “place and move objects” tools, to literally a fully functional 3D mesh sculpting app. All you really need to do is design and implement the UI.

Based on the design tools I have built in the past, I can say with some certainty that the current Modeling Mode Tools are probably not exactly what you will need in your own app. They are a decent starting point, but really what I think they provide is a reference guide for how to implement different interactions and behaviors. Do you want a 3D workplane you can move around with a gizmo? Check out UConstructionPlaneMechanic and how it is used in various Tools. How about drawing and editing 2D polygons on that plane? See UCurveControlPointsMechanic usage in the UDrawAndRevolveTool. An interface for drawing shortest-edge-paths on the mesh? USeamSculptTool does that. Want to make a Tool that runs some third-party geometry processing code, with settings and a live preview and all sorts of useful stuff precomputed for you? Just subclass UBaseMeshProcessingTool. Need to run an expensive operation in a background thread during a Tool, so that your UI doesn’t lock up? UMeshOpPreviewWithBackgroundCompute and TGenericDataBackgroundCompute implement pattern, and Tools like URemeshMeshTool show how to use it.

I could go on, for a long time. There are over 50 Tools in Modeling Mode, they do all sorts of things, far more than I could possibly have time to explain. But if you can find something close to what you want to do in the UE Editor, you can basically copy the Tool .cpp and .h, rename the types, and start to customize it for your purposes.

So, have fun!

Procedural Mesh Blueprints in UE4.26

no static meshes were cooked in the making of this level. Click to play video.

In my previous tutorial, I showed you how to do runtime mesh manipulation in Unreal Engine 4.26 using various components (UStaticMeshComponent, UProceduralMeshComponent, and USimpleDynamicMeshComponent) by way of the GeometryProcessing plugin’s mesh editing capabilities and a sort of “wrapper” Actor called ADynamicMeshBaseActor. An obvious thing that you might want to use this machinery for is to do procedural geometry generation, either in-Editor or in-Game. And since ADynamicMeshBaseActor exposed Blueprint functions for things like mesh generators, Mesh Booleans with another ADynamicMeshBaseActor, and so on, one could imagine building up a procedural system where you generate Actors and combine them to build up complex geometry.

Here’s the problem though: Actors are expensive. Say you want to do something like use an L-System to create plants, or buildings, or whatever. These systems tend to involve lots of small meshes. Making an Actor for each of those small meshes would be…painful.

So, in this tutorial I’m going to show you one way to implement a more effective procedural mesh generation system in Blueprints. I’m not sure this approach is the best way to do it, and it has some serious pitfalls. But the result is that the small level you see on the right is 100% generated by Blueprints - there is not a single static mesh in this project. All the geometry is built up by combining simple primitives, doing operations like Booleans and mesh-wrapping and applying displacement noise, and there is even a simple all-in-Blueprints scattering system for placing rocks on the asteroids. The textures are not procedural, I made them in Quixel Mixer. But they are applied without UV maps, so that’s kinda procedural! And I threw in a little Niagara particle system at the end, to spice up your escape from the Asteroid.

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games. However, gradientspace.com is his personal website and this article represents his personal thoughts and opinions. In particular, this tutorial code and content is not part of Unreal Engine, and it isn’t supported by Epic Games.)

Getting and Running the Sample Project

Before we begin, this tutorial is for UE 4.26, currently in Preview release (Preview 7 at time of writing). You can install the Preview binaries from the Epic Games Launcher.

The project for this tutorial is on Github in UnrealProceduralMeshesDemo repository (MIT License). I did not include this in the same repository as my previous tutorials because there are ~100mb of binary files. In UE 4.26 this project will probably only work on Windows due to the inclusion of the DynamicSDMCActor class in the RuntimeGeometryUtils plugin. However I did not use any DynamicSDMCActors in this project, so you should be able to make it this demo work on OSX/Linux by deleting the DynamicSDMCActor .cpp and .h files - see the notes at the end of the previous tutorial (If you try that and it works, please send me a note so I can mention it here).

Once you are in the top-level folder, right-click on ProceduralMeshesDemo.uproject in Windows Explorer and select Generate Visual Studio project files from the context menu. This will generate ProceduralMeshesDemo.sln, which you can use to open Visual Studio. You can also open the .uproject directly in the Editor (it will ask to compile), but you probably will want to refer to the C++ code for this tutorial.

Build the solution and start (press F5) and the Editor should open into the sample map. You can test the project in PIE using the large Play button in the main toolbar, or click the Launch button to build a cooked executable. This will take a few minutes, after which the built game will pop up in a separate window. Try to escape the level! You’ll have to press Alt+F4 to exit as there is no menu/UI.

UGeneratedMesh

At the end of the last tutorial, ADynamicMeshBaseActor had some basic Blueprint functions you could use to do single mesh operations, like subtract another Actor, and so on. But to do real mesh generation, we need lots of temporary meshes. Consider something trivial like a “stairs generator”. In it’s simplest form, you would make a box, and then append a bunch of translated copies of that box, each shifted up-and-forward from the last. What I want to be able to do is have a BP_ProceduralStairs Actor, that has parameters for # of steps, width, height, etc, and it’s Blueprint does the mesh generation.

To do this kind of thing, we’re going to need temporary meshes. I want to make a temporary mesh, append a bunch of other meshes to it (which might be temporary meshes themselves), and then transfer that mesh to my ADynamicMeshBaseActor’s Source Mesh. So the question is, how to handle the temporary meshes in Blueprints? In Normal C++ we would just make FDynamicMesh3 objects, use them, and throw them away. But in Blueprints, we can only “use” the meshes by passing them between Blueprint functions. And to pass data between BP Functions, we either have to have them be UStructs or UObjects.

The issue with using UStructs is that Blueprints pass UStructs by value, and are very liberal with making copies of UStructs. So what that means is, if we put our FDynamicMesh3 inside a UStruct, it gets copied. A lot. There are ways to cheat to avoid the copies, like stuffing non-UProperty pointers inside the structs, but to use the cheats safely means that the person making the Blueprints has to understand what going to happen in C++. This is a Bad Idea.

So, our other option is a UObject. UObjects are much heavier than UStructs, and they are managed via garbage collection. What that means is, when a UObject is no longer referenced by any UProperties, it will be deleted (eventually). This garbage collection is going to cause some complications. But otherwise, this approach basically works. I have created a class UGeneratedMesh that is similar to the core of ADynamicMeshBaseActor - it has a FDynamicMesh3, as well as FDynamicMesh3AABBTree and TFastWindingTree for spatial queries.

What it doesn’t have is a Material, Transform, or any of that stuff. It’s just a container for a mesh, with a set of UFunctions to manipulate that mesh. The set of functions is quite large, it includes a bunch of primitive generation functions (Box, Sphere, Cylinder, Cone, Torus, Revolves, and Extrudes), functions to Append and Boolean other UGeneratedMeshes, Cut with a plane, Mirror, Solidify, Simplify, Transform, Recompute Normals, and various Spatial Query functions. It can do a lot of things! And you can spawn them in Blueprints as needed, to do node-graph-style geometry creation.

My basic stacked-boxes Stairs Generator is below. This is all happening in the Construction Script on an ADynamicMeshBaseActor Blueprint called BP_ProceduralStairs in the sample project. I have two temporary meshes, Step Mesh and Stairs Mesh. The Append Box function adds a box to the Step Mesh, and then the Append Tiled function adds Step Mesh to Stairs Mesh multiple times, applying the input Transform each repetition. Finally Copy from Mesh is a function of the ADynamicMeshBaseActor, that copies the UGeneratedMesh geometry into the Actor, which then goes on to it’s Component (I will use ProceduralMeshComponent for everything in this tutorial, we’ll get to that).

View fullsize

All the parameters above are exposed on the Actor, so in the Editor I can select a BP_ProceduralStairs and change it’s various dimensions and number of steps in the Actor Details panel.

Our Nemesis: Garbage Collection

There is one fly in the ointment here, though. In the BP screenshot above, I cropped off the top. That’s where I need to create the UGeneratedMesh instances for StepMesh and StairsMesh. The standard way to do this would be to use the BP version of the C++ NewObject<> function, which spawns a new UGeneratedMesh UObject. The Blueprint nodes below-left do that (click to enlarge). This works fine, until you open up the Task Manager and look at memory usage as you drag one of the parameters in the Details Panel. Look at it go - hundreds of megabytes in a few seconds!

View fullsize

What is happening here is that the temporary UObject meshes we spawned with Construct Generated Mesh are not deleted when the Construction Script completes. They become unreferenced, but they will hang around until the Garbage Collector (GC) runs, which is about once a minute in UE4.26. And sure enough, if you wait for a while, memory usage will drop back down. But this is not acceptable. We could force the GC to run, but this is not a good practice, and creating and then destroying all these UObjects is a lot of overhead.

Generated Mesh Pooling

What to do? Well, this is not a new problem. It comes up all the time, and particularly in procedural systems where you are going to do the same thing over and over as the user interactively changes some parameter. The general way to address this is Caching of some kind or other, and for this specific situation the standard strategy is Pooling. Which means, basically, re-use the things you have already created/allocated instead of making new ones all the time.

Re-using UObjects is a bit tricky in Blueprint Construction Scripts, where we ideally want to do our mesh generation (otherwise it will not be visible in the Editor). We can’t just add some generated-mesh pool UObject in the Construction Script because it will get re-created on each run. So, I put it in the ADynamicMeshBaseActor. There is a UGeneratedMeshPool class, and a UProperty instance of this, but it is not exposed to Blueprints directly. Instead there is a BP function ADynamicMeshBaseActor::AllocateComputeMesh() which will give you a UGeneratedMesh you can use, either by allocating a new one or providing one from the pool. So now our Blueprint looks like below, and we see that memory usage stays reasonable as we edit an instance of the BP_ProceduralStairs Actor:

View fullsize

View fullsize

But, we’re actually not done yet. If you look up at the Stairs Generator BP, you’ll see that the Exec path also goes off to the right. What’s over there? Well, generally when you do Pooling you have to explicitly give any objects you took back to the Pool, and it’s no different here. ADynamicMeshActor also has several functions to return the UGeneratedMesh’s we have taken ownership of. These must be called at the end of the BP, otherwise the mesh will hang around forever! The screenshot below shows two possible paths, there is a Release Compute Meshes function that lets you explicitly release meshes (there is also Release Compute Mesh for a single mesh), as well as a simpler Release All Compute Meshes function that tells the Pool to take back all the meshes it has given out. I tend to use this one when generating meshes in construction scripts, as it requires the least effort, but be aware that it means you can’t hold on to any of the meshes.

This “Return to Pool” mechanism is the one big gotcha of this UGeneratedMesh architecture. I haven’t figured out a way around it. If you forget to release your compute meshes, things could spiral out of control quickly! So, to try to avoid catastrophe, if the pool grows to over 1000 UGeneratedMeshes it will clear the pool and run garbage collection.

DynamicMeshBaseActor Improvements

This tutorial will use the ADynamicMeshBaseActor I created in the previous tutorial to represent procedural meshes in the Level. I have made some improvements, though. First of all, I grouped the various UProperties under a DetailsView category called “Dynamic Mesh Actor”. I have added a new Source Type called Externally Generated. This tells the Actor that you will populate it’s Source Mesh yourself - if you don’t set it to this value, then it will overwrite your generated mesh with a Primitive or Import.

I also exposed a new Runtime Collision mode named Simple Convex Hull. When set to this mode, the DynamicPMCActor subclass will calculate convex hull “simple collision” for the mesh whenever it is updated. This convex hull will optionally be simplified to the Max Hull Triangles triangle count (set to zero to use the full hull). If you use this mode, then it is possible to enable Simulate Physics on the ProceduralMeshComponent and it will work!

We will use this option in a few places. Note, however, that generating the convex hull can be very expensive if the input mesh is large - ie several seconds if you have many thousands of triangles. It might make sense to have some thresholds, ie don’t compute the hull if the mesh is too large, or randomly sample a subset of vertices. I haven’t done any of that, but I would take a PR!

Note that I exclusively used DynamicPMCActor in this project. This is because only the ProceduralMeshComponent supports runtime cooking of Simple or Complex collision, and only with PhysX (the default physics library in UE 4.26 - for now!).

UGeneratedMesh Procedural Mesh Generation API

View fullsize

I won’t say much about the actual UGeneratedMesh Blueprint API, you can skim the header or browse the Generated Mesh category in the BP Editor (search “generatedmesh” in the BP function search bar) to see what is available. There is no particular strategy for completeness, I implemented what I needed to make the tutorial. Most of the functions are just wrappers around calls to the GeometryProcessing plugin.

One slightly unusual thing I did in the BP functions is have most of them return a UGeneratedMesh that is actually just the input mesh. It’s very important to note that this is not a copy. That’s why the output pin is labeled “Input Mesh”. Because a lot of the mesh processing is a sequence of functions applied to the same UObject, I found that this let me make BPs which were much clearer to read, vs having a far-away output feeding multiple inputs. However these output pins are optional and you don’t have to use them!

Another important note: there are not many safety checks in these functions. If you pass in arguments that will produce a huge multi-gigabyte mesh, the code will happily do it and you will have to kill the Editor. It’s kind of tricky to put in these kinds of limits, because what one person considers reasonable may be an eternity to another.

Blueprint Function Libraries

I have placed most of the mesh editing functions directly on UGeneratedMesh. However, this strategy will lead to enormous classes which can be difficult to manage. It also doesn’t work to “extend” the base class with additional functions, which is particularly a challenge if you have your own third-party libraries and you want to use them in some BP function implementations. To handle this kind of situation, we can use a Blueprint Function Library. Making a BP Library is very simple, just define a C++ class that subclasses UBlueprintFunctionLibrary, and then add static UFunctions that are BlueprintCallable. Those functions will then be available in the BP Graph Editor.

I did this for the various mesh deformers that are used below (Sin Wave Displacement, Perlin Noise, Mesh Smoothing, etc). The static UFunctions functions are in the UGeneratedMeshDeformersLibrary class. Organizing things this way allows you to add your own functions that operate on a UGeneratedMesh, and keep your C++ code better-organized (I should have done more of the UGeneratedMesh API this way!)

Blueprint Procedural Mesh Generators

Ok, on to the tutorial. I have already explained the Stairs generator above. In the tutorial there are various other Procedural Mesh BP Actors that I will briefly explain here

BP_Wall

This Blueprint generates a basic rectangular box with configurable width/height/depth, and an optional angled top, created using a plane cut. The angled top allows this BP_Wall to also be used for creating ramps. There really is not much to it. Most of the nodes below are converting the input parameters into the necessary input vectors, rotations, transforms, and so on. So far I have found that this part tends to be more work than setting up the actual mesh operations. That said, I’m also not a Blueprint guru so maybe there are more efficient ways to accomplish some of these basic geometric constructions.

The only thing I wanted to point out below is the Set To Face Normals call. In most of the editing operations, I am not automatically recomputing normals. This is to avoid the cost of repeated normal computation if you are chaining multiple operations together. Note that Copy from Mesh has a Recompute Normals boolean. This does work, but it does not have the ability to compute normals with creases based on a threshold angle, which can be done with the UGeneratedMesh function SetToAngleThresholdNormals (which is not necessary on a wall like this, where Face Normals are sufficient, but I used it in various others below)

View fullsize

BP_Rock

This is another relatively simple generator, that creates a reasonable rock or boulder by displacing the vertices of a sphere using Perlin Noise. Hard Normals are then computed with an angle threshold, which produces some sharp edges and, combined with a nice triplanar texture, makes for a reasonably convincing rock. This is quite a cheap generator, and with a bit of additional effort the rocks could be randomly scaled, and/or multiple frequencies of Noise could be used to produce a wider range of shapes. Note that the Noise is defined by an explicit RandSeed parameter - if you don’t change this, you’ll get the same rock every time. In this kind of procedural generator, we generally want reproducible results so it is necessary to use explicit random seeds.

For these rocks, I have set the Collision Mode to Simple Convex Hull in the Dynamic Mesh Actor properties. This allows the rocks to be simulated, which is why they can drop out of the pipe and roll down the stairs.

Note that in the BP below, the construction script just calls a BP-defined function called Generate Rock. This is a useful way to organize procedural mesh generators, and allows for “sharing code” between the Construction Script and Event Graph (a common thing to want in procedural generators).

View fullsize

The pipe the rocks fall out of is also procedurally generated in BP_RockEmitter, by creating two cylinders and then subtracting a third. There is nothing particularly new in that generator that isn’t in the others, so I did not include it here. BP_RockEmitter also has some Tick functionality, as it spawns new instances of BP_Rock at regular intervals, but this is pretty standard Blueprint gameplay stuff so I won’t explain it here.

BP_DynamicBridge

In the tutorial project level, once you’ve made it past the barrier wall, you’ll have to correctly time a run across a walkway that cycles back and forth to the far platform, as shown on the right. This is a procedural mesh being regenerated each frame, with the “bridge length” parameter being driven based on elapsed game time.

The geometry generation is not that complex, just a box with two Sin wave deformers applied to it. However the BP is structured somewhat differently than BP_Rock, in a way that I think is better. The geometry is created in a BP Function called Generate Bridge. However instead of allocating and releasing it’s own compute mesh, Generate Bridge takes the UGeneratedMesh as an argument, and returns it at the end of the function. This means that if you wanted to re-use this code, you can easily cut-and-paste it into any other BP without having to worry about the Copy from Mesh and Release All Compute Meshes at the end of Generate Rock above (which might conflict with other geometry generation you want to do).

Another benefit to putting the generation code in a BP Function is you can then easily run the same code in-Editor and in-Game. The Construction Script (below-middle) and the Event Graph Tick version (at the bottom) are basically the same, except for the time-dependent animation of the length parameter.

View fullsize

BP_BlobGenerator

The Blueprint that creates the two large asteroid pieces is BP_BlobGenerator, and it has quite a lot going on. I won’t fully explain every node, it but here’s a simplified description of what happens along the exec flow below

1. Create a mesh called Subtract Shape (a sphere in this case)

2. Create another Sphere and deform it with two Sin Wave deformers, this is our final Accumulated mesh we will build up

3. For Loop to repeat the following “NumBlobs” times

   1. Generate a random point on a sphere

   2. find the closest point on the Accumulated mesh

   3. subtract the Subtract Shape from the Accumulated mesh at that point, with a random scale

4. Update the Actor’s source mesh

5. Optionally apply the Make Solid BP function below

By default, BP_BlobGenerator has no collision enabled, however the asteriods in the tutorial level are configured to use Complex as Simple collision. This works quite well to create landscape-type elements that are not too high-resolution. In the level, I increased the simplification triangle count to 4000, because at large scale things felt a bit too triangulated. A pass of mesh smoothing might also have helped to reduce that.

View fullsize

The Make Solid function is straightforward, basically we are going to copy the current Source Mesh from the Actor, call the Solidify function, apply Perlin noise displacement if necessary, and then Simplify the result and re-update the Actor Source Mesh. This generates a more compelling rock-like/organic object, by removing all the sharp creases and “perfect” geometry.

One issue with using this BP in practice is that the Solidify and Simplify functions are (relatively) slow, for real-time use. This is all vastly more expensive than BP_Rock, for example. So, in practice when I am positioning and configuring one of these Actors, I would disable the Solidify setting in the “Blob Generator” DetailsView properties, and then toggle it on to see the final result. However I did one other thing in this BP, which is to enable the “Call in Editor” flag on the MakeSolid BP function (shown below-right). This leads to the BP Function being exposed as a button labeled “Make Solid” in the Blob Generator Details panel section (shown below-left). If you click that button, the Make Solid function will be applied. This is why I in the Make Solid function I initialized a GeneratedMesh from the current Actor Source Mesh - so that it can be called without re-running the Construction Script.

View fullsize

These kinds of UI-exposed functions are extremely useful as a way to extend the capabilities of an Actor in the Editor. For example it might be nice to have a button on the ADynamicMeshActorBase that could emit a new StaticMeshActor - it would effectively turn these Procedural Mesh BPs into asset authoring Tools in the Editor. Maybe something to tackle in the future. However, do be aware that the next time the Construction Script runs it will wipe out any result created by incrementally updating the Source Mesh!

BP_SpaceShip

View fullsize

At the end of the tutorial video, the character jumps off the edge of the asteroid, lands on a ship, and flies away. Making this ship was the most time-consuming part of creating the demo, but in many ways it’s both visually and technically the least interesting. The BP is below, you can click to see a larger version, but you’ll discover that’s really just a straight-ahead generate-primitives-and-append-them situation. The generator could be parameterized in many ways, which might make it more useful. But I think I would have been able to hand-model a more interesting ship in much less time.

This BP does have a nice Niagara particle system attached, though, that emits particles from the rear engine when they fire up. I followed the “Create a GPU Sprite Effect” tutorial on from the UE4 documentation to start, and then made changes. It was very straightforward and looks pretty good, I think.

View fullsize

BP_RockScatter

This Actor is the most complex in this tutorial as it isn’t really a single “object”, but rather a generator for a set of rocks covering the asteroid surface. The basic idea here is not complicated - I am going to generate random points on a 3D plane above the asteroid, shoot rays downwards, and if the rays hit a relatively flat spot, I’ll add a new randomly-deformed rock at that location.

That might sounds costly, but actually this actor is surprisingly inexpensive - it updates very quickly as I drag it in the Editor viewport. This is because the computation involved amounts to a raycast and then a mesh copy. It’s much cheaper than even a single mesh boolean, let alone voxel operations or simplification. All the rocks are accumulated into a single mesh, so this doesn’t add a tick or draw call per-rock (however it also means there is no instanced rendering). That said, if I crank up the rock count, things will start to get chunky (on my quite powerful computer, 50 rocks is interactive but 200 takes a second or so to update).

Note that this definitely isn’t the most efficient way to implement scattering like this. At minimum all the ray-shooting and mesh generation/accumulation could easily be ported to a single C++ UFunction, and much of it done in parallel. But it’s kind of nice to prototype it in Blueprints, where an artist can easily go in and make changes.

View fullsize

You might note in the gif above there is a yellow box that is moving with the scattered rocks. This is a Box Collision component that I added in the Actor to define the scattering bounds, as shown in the BP editor screenshot to the right. The ray origin points are randomly generated on the top face of the box, and shot down the -Z axis. The box dimensions/etc could have been done with BP parameters, but having a visual box is a nice design guide and helps with debugging.

The scattering in the Actor BP is computed in the Do Scatter function, the Construction Script just calls this, like we saw in other examples above. Most of this BP is actually just generating the ray origin and mapping between coordinate systems. Basically we generate one rock and then inside the For loop, at each valid intersection point, we apply a random rotation and scale to break up the repetition. Although Append Tiled is used, it’s called once for each rock, with 1 repeat - so in this context it’s just a way to append a single mesh, because we don’t have an Append Once function. Finally in the bottom-right we return the accumulated Scatter Objects mesh.

View fullsize

One question is, what to scatter on. We could have used world linetraces to find hits, but then we would have had to filter out all the non-asteroid level elements. Instead I used the ADynamicMeshBaseActor spatial query function IntersectRay. The BP_RockScatter has a public array UProperty of ADynamicMeshBaseActor targets, as shown on the right. The Find Intersection Point BP function (pasted below) calculates the nearest ray-intersection point on each of these objects and returns the nearest point. Although I have hardcoded the ray direction in this point, that could easy be exposed as an argument, making this a very general BP function (that doesn’t rely on physics!)

View fullsize

One important note about working with this BP in the Editor. The rocks only update when the Construction Script runs. So, if you change the Asteroids, you need to force the Scattering to be recomputed by changing a setting of the Actor instance (ie, “jiggle it” a bit, change the Scatter Count, etc).

UVs and Triplanar Textures

I have avoided the question of UVs so far, because UVs potentially make all this procedural-mesh stuff a lot more complicated. The basic shape-generator functions for spheres, boxes, toruses, etc, all generate decent UVs. The underlying generators have more UV options that could be exposed. Boolean operations will combine UVs properly, and perations like Plane Cut will (for example) generate UVs on the cut surface, and there are controls for those UVs in the underlying C++ code (also not BP-exposed here). However none of these operations will update the UV Layout, ie make sure that islands are unique/etc. And there is no way (currently) to recompute UVs for an object after something like the Solidify operation. (This can be done in the Editor, but it requires calls to Editor-Only code, and only works on Windows currently).

This limits the options for texturing, but again, in a procedural context this is all pretty common. If you want to generate procedural worlds, you aren’t going to be hand-painting them. The most basic procedural texturing one can do is simply to apply tiled UV maps, based on the UV set. This can work surprisingly well if the “scale” of the UV islands on the mesh are all relatively similar, however (for example) if you subtract a small sphere from a big one, this won’t be the case by default. The UVs in the subtracted-small-sphere area will be denser, and so the texture pattern will be different sizes.

An alternative is to use local or world-space Projection. What this means at a conceptual level is, we take a geometric shape with known “good” UVs, eg like a plane/box/cylinder/sphere, and put the texture map on that shape. Then to find the color at a point on our detailed shape, we map that position onto the simple shape (eg by casting a ray, nearest point, etc) and use the color/etc at the mapped point. So for example with Planar Projection, to find the color for point P we would project P onto the tangent axes of the plane, ie U = Dot( P-PlaneOrigin, PlaneTangentX ) and V = Dot( P-PlaneOrigin, PlaneTangentY ), and then sample the Plane’s Texture Map at (U,V).

Planar Projection is cheap but only works if your surface is basically pointing at the plane, otherwise it just kind of smears out. A more complex version is TriPlanar Projection, where you have 3 planes and use the surface normal to choose which plane to project onto, or as a way to compute a blend weight between the 3 colors sampled from each plane. This works particularly well for things like rocks, cliffs, and so on. In UE there are special Material nodes to create TriPlanar texture, called WorldAlignedTexture, WorldAlignedNormal, etc (this technique does work for both world-space and local-space, despite the name). The Quixel website has an excellent tutorial on setting up these kinds of Materials. In this tutorial I have used TriPlanar materials extensively, for all the rocky surfaces. Quixel’s Megascans library has tons of great tileable textures to use with TriPlanars (all free if you are using UE4). And you can also use Quixel Mixer to create new ones - I made the textures in the tutorial sample by messing around with the Mixer sample projects.

Finally it is also possible to procedurally generate fully 3D materials, ie 3D patterns that the mesh “cuts through” to define the surface texture. These can work quite well if you are going to cut into the shape using booleans. I have used one of these for the destructible brick wall, but I won’t say this is necessarily the greatest example - I am a novice at creating UE Materials!

Gotchas, Pitfalls, Caveats, and so on

I quite enjoyed playing with procedural shape generators like this in the Editor. I’m not a great artist, so being able to generate shapes and mash them up let me build a level I probably would not have put in the effort to model by hand. But, I do want to be super clear that although the approach to procedural content generation that I have outlined here might be fine for a demo or small indie game, it won’t scale up to a large procedural world. There are some major problems.

For one, UProceduralMeshComponent is serialized in the Level. So every time I save the level, all my generated PMCActor meshes are being saved, and when I restart the Editor they are de-serialized, right before my Construction Scripts run and regenerate them all! It’s not only inefficient (it takes quite a long time), it also requires a lot of disk space - the AA_AsteroidLevel.umap file is 38MB, just for this small level. And if the content is all in the Level, you can’t have someone else working on it, as you can’t merge changes to the binary .umap file. So, saving and loading the Level is a bottleneck. (Note that this would not be an issue if the Actors were only spawned at runtime)

Second, I relied very heavily on Construction Scripts. This is mostly fine, as the objects are generally independent. However, it is a major problem for the BP_RockScatter scattering Actor. The issue is that this Construction script must run after the scripts for the Asteroids, or there is nothing for the raycasts to hit. However, it is not possible to explicitly specify the ordering of Construction scripts. So it’s easy for this to break. If you google you’ll find various tricks, like order of adding to the level, naming, etc, that can make this work, but these are not guarantees and the ordering could easily change in future Engine versions. If you wanted to build a complex sequence of procedural generators, with dependencies on eachother, this would not be possible to do with Construction scripts. It is possible to better handle these kind of dependencies at runtime, by making the generation dependent on events fired between Actors. But then you have to PIE to see what your generators are doing.

Third, it’s pretty easy to accidentally lock up the Editor when playing with these Blueprints. The computation all happens on the main thread, and cannot be interrupted, so if you do something that is going to take 20 minutes (or 20GB of RAM) to compute, you’ve just got to wait. In particular, dragging sliders in the Details panel is a problem, it tends to lock things up while it recomputes the BP for each slider update. I got in the habit of typing in new values instead of just scrubbing to see what happens, like you might in a Material.

Basically, we’re trying to wedge a procedural geometry dataflow graph into a system that was not designed for this. A real procedural node-graph system for doing expensive geometry operations has a very different underlying architecture than a runtime gameplay framework like Blueprints. For example, a procedural node-graph system usually automatically handles things like our mesh pool, caches expensive computations, evaluates nodes in parallel when possible, and so on. Then again, those DCC-tool node-graph systems don’t work at Runtime…

Wrapping Up

That’s it for this tutorial. If you make neat things with procedural meshes using the system I have developed here, please @ me on twitter (@rms80) with screenshots, comments, and suggestions, or send an email.

If you want to dive deeper into Procedural Content Authoring/Generation inside UE, I highly recommend watching the Getting Started with Procedural Mesh Generation twitch stream by Arran Langmead (twitter). In this video Arran explains how he builds a procedural tree generator using the basic UProceduralMeshComponent API (which allows you to build up meshes directly from vertex positions and triangle index arrays). There is an accompanying written article which walks through much of the same content on 80.lv. Unlike myself, Arran is a UE master and his tree sample can show you how to do awesome things like make procedural shaders and procedurally animate generated meshes with materials.

After I watched Arran’s video I realized there is so much more that could be added to UGeneratedMesh, particularly with vertex colors. I have not made any effort to support vertex colors. But, FDynamicMesh3 supports vertex colors, and it would not be difficult to add vertex color support so that (for example) vertex colors on different parts of a Boolean are preserved, or to add BP functions to calculate vertex colors from spatial fields, 3D noise, etc. Exciting!

Mesh Generation and Editing at Runtime in UE4.26

In my last tutorial, I showed you how to use the new experimental GeometryProcessing plugin in UE4.26 to do useful meshy things like mesh generation, remeshing, simplification, and Mesh Booleans (zomg!). When people first learn that we are building these capabilities in Unreal, one of their immediate questions is usually “Can I use it in a game?”. The short answer is, yes. However there is no Blueprint API to that plugin, so there are some hoops to jump through to do it.

A related question that comes up very frequently is how to implement runtime mesh creation in a UE4 game or application. UProceduralMeshComponent (API docs link) is historically how one would do such a thing in Unreal Engine. As of UE4.25, it is now also possible to “build” and update a UStaticMesh at Runtime, which can then be used in UStaticMeshComponent/Actor. So we now have a new question, which one should you use? In addition, there are third-party solutions like RuntimeMeshComponent (link) that provide more functionality than UProceduralMeshComponent and might be a better choice in some situations. (For the rest of this tutorial I am going to abbreviate UProceduralMeshComponent as PMC and UStaticMesh/Component as SMC, to save my fingers).

Unfortunately there is no “best” option - it depends on what you need. And it’s not immediately obvious how to hook any of them up to our GeometryProcessing plugin, which uses FDynamicMesh3 to represent meshes without any connection to Components or Actors. So, in this tutorial I will show you one way to implement runtime-generated-and-edited meshes that will work with any of these options.

The video above-right shows a small “runtime geometry gym” demo that I built using the Actors and utility code in this tutorial. As you can see there are Booleans, mesh operations, and some spatial-query demos. These are just a few things I exposed via Blueprints (BP), and by the end of this tutorial you should understand how it is very straightforward to expose other GeometryProcessing-based mesh editing code on the ADynamicMeshBaseActor I will describe below.

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games. However, gradientspace.com is his personal website and this article represents his personal thoughts and opinions. About triangles.)

Translation for Chinese Users: https://zhuanlan.zhihu.com/p/345724236

Getting and Running the Sample Project

Before we begin, this tutorial is for UE 4.26, currently in Preview release (Preview 4 at time of writing). You can install the Preview binaries from the Epic Games Launcher.

The project for this tutorial is on Github in the UnrealMeshProcessingTutorials repository (MIT License), in the UE4.26/RuntimeGeometryDemo subfolder. Unfortunately in UE4.26 this project will only work on Windows. It should be possible to get this tutorial working on OSX or Linux with some selective deleting, I will describe this at the end of the post. If you don’t want to check out with git, you can grab a zip of the current repository.

Once you are in the top-level RuntimeGeometryDemo folder, right-click on RuntimeGeometryDemo.uproject in Windows Explorer and select Generate Visual Studio project files from the context menu. This will generate RuntimeGeometryDemo.sln, which you can use to open Visual Studio. You can also open the .uproject directly in the Editor (it will ask to compile), but you probably will want to refer to the C++ code for this tutorial.

Build the solution and start (press F5) and the Editor should open into the sample map. You can test the project in PIE using the large Play button in the main toolbar, or click the Launch button to build a cooked executable. This will take a few minutes, after which the built game will pop up in a separate window. Run around and shoot the walls! You’ll have to press Alt+F4 to exit as there is no menu/UI.

The Code

There are two sides to this tutorial. First, I will describe an architecture for at-runtime dynamic/editable mesh Actors implemented in C++, and then the sample project that uses these Actors with Blueprints to do interesting things. None of the “game logic” is in C++, just the core functionality. I have put this all a plugin named RuntimeGeometryUtils, which you could easily copy to your own projects. Just to mention up front, in RuntimeGeometryUtils I have also included updated versions of DynamicMeshOBJReader/Writer from my previous tutorial, but I have changed the API to be static functions.

PMC or SMC?

If you are going to set about building dynamic in-game geometry, the immediate question is whether to use UProceduralMeshComponent (PMC) or UStaticMeshComponent (SMC). There are various small differences between these two, but the biggest is in terms of performance. To update a mesh at runtime, it needs to be “built”. By this we meant that the Rendering representation of the mesh needs to be created or updated. Unreal does not directly render from the Sections in a PMC or the FMeshDescription in a SMC. For any UMeshComponent (of which both PMC and SMC are), a FPrimitiveSceneProxy subclass is created which is the rendering representation of the Component. That Proxy will create one or more FMeshBatch from the Component data.

In PMC this is relatively straightforward and I would suggest you just go skim the code that does it in ProceduralMeshComponent.cpp, the FProceduralMeshSceneProxy class is at the top. You will see that in the constructor, FProceduralMeshSceneProxy converts the FProcMeshSection’s that you create externally and initializes a FStaticMeshVertexBuffers and FLocalVertexFactory. These store things you would expect the GPU to need, like vertex positions, triangle index buffer, Normals and Tangents, UVs, Vertex Color, etc. To the GPU this data is not different between a PMC or SMC, the only difference is how it gets there.

SMC is much more complex. I am playing a bit loose with terminology here, because a UStaticMeshComponent does not store a mesh itself - it references a UStaticMesh, and the UStaticMesh stores the mesh. Until UE4.25 it was not possible to update a UStaticMesh at runtime. This is because traditionally your “source mesh” in the Unreal Editor, stored as a FMeshDescription inside UStaticMesh, is “cooked” into a preprocessed, optimized “rendering mesh” that is used to initialize the FStaticMeshSceneProxy (done in StaticMeshRender.cpp). The source FMeshDescription is not used after cooking, so it is stripped out in your built game. This cooking process, kicked off by UStaticMesh::Build(), depends on various Editor-only functions and data, and that’s why you couldn’t update the UStaticMesh geometry at runtime.

But, in 4.25 a new function was added - UStaticMesh::BuildFromMeshDescriptions(). This function takes a list of FMeshDescriptions and initializes the rendering mesh data, allowing a UStaticMesh to be built at runtime. This build is not the same as the Editor-only ::Build() path - it skips various complex steps that are too slow to do at runtime (eg build Distance Field Lighting data) or not useful (eg generate lightmap UVs, which would be useless as you can’t bake new lightmaps at runtime).

Calling BuildFromMeshDescriptions() is more expensive than updating Sections in a ProceduralMeshComponent. The trade-off is that you can re-use the generated UStaticMesh in multiple StaticMeshComponents (and may even get instanced rendering), while if you want to have multiple of the “same” PMC, you need to copy the mesh into each one. In addition you get extra rendering features with SMC. For example the FProcMeshVertex used in the PMC only supports 4 UV channels, but a UStaticMesh supports up to 7. UStaticMesh also supports LODs and Sockets, and generally SMC is better-supported throughout the Engine.

One more fundamental difference has to do with how these different types use the renderer. PMC uses what’s called the “Dynamic Draw” path, which means it rebuilds and re-submits FMeshBatches every frame. This basically tells the renderer “my vertex/index buffers might change at any frame, so don’t bother caching anything” and this has a peformance cost. SMC uses the “Static Draw” path, which tells the renderer that the render buffers are not going to be changing and so it can do more aggressive caching and optimization. If you are interested in more details here, Marcus Wassmer gave an excellent GDC 2019 talk on the current UE4 Rendering Pipeline..

These are not the only differences, however in terms of at-runtime generated meshes, this is the core trade-off. SMC will give you better rendering performance but has a higher up-front cost. So if you are just loading generated meshes, or are “done” dynamically editing or changing a mesh, you will benefit from building it as an SMC. But if you are actively changing a mesh, you will really suffer if you are updating a SMC every frame. As a simple test, I used the infrastructure I will describe below to re-generate a sphere every frame, at “tessellation level 32”, which generates 2046 triangles and 1025 vertices. Using PMC this runs at 90-100fps in PIE. With SMC it drops down to 30fps. If I crank up the tessellation to 128 (32k triangles), it’s still hitting about 15fps with PMC, while with SMC it’s an unworkable 3fps.

A Third Option: USimpleDynamicMeshComponent

Having to deal with two different Components does make things complicated…and I’m about to make it worse! PMC has a fundamental limitation in that it cannot have split normals, UVs, or other attributes at a vertex. So if you have a cube with connected mesh topology - ie it has no boundary edges - but 3 normals at each corner vertex, or a separate UV chart/island for each face, you have to split that cube up into 6 rectangles before you initialize the PMC. This is because the PMC wants to be as efficient as possible at initializing the RenderProxy, and the GPU doesn’t support split-anything. Splitting up vertices and rewriting triangle indices is complicated and would make the PMC API much more complex, so you have to do it yourself.

But, this means that the PMC is not suitable to directly use for any kind of mesh editing. For example lets say you want to plane-cut a cube and fill the cut surface. Well, if you were to try to cut the PMC sections directly, you don’t actually have a cube, you have 6 disconnected triangle patches. So now instead of getting a closed boundary loop after the cut, which is ideal for hole-filling, you get some 3D lines that need to be chained up to identify the hole. This is all very bad for editing reliability. Similarly if you pull on a “cube” corner, you’re just going to create a crack. I could go on…just trust me, it’s a nightmare.

So, to implement the Mesh Modeling Editor Mode in UE 4.25, we introduced another type of mesh Component, USimpleDynamicMeshComponent. This component is like a PMC in that it uses the Dynamic Draw path and is designed to be fast to update. However unlike the PMC, it stores a more complex mesh representation that supports split-attributes at vertices, and internally handles rewriting that mesh as something suitable for the GPU. And what is this more complex mesh representation? It’s a FDynamicMesh3 of course.

(Why “Simple”? Because there is another variant - UOctreeDynamicMeshComponent - that is designed for efficiently updating sub-regions of huge meshes. That one is beyond the scope of this tutorial.)

USimpleDynamicMeshComponent (let’s call it SDMC) has many features that PMC lacks that are nice for interactive mesh editing situations. For example it supports overriding the material on a subset of triangles, or hiding them, without re-structuring the mesh. It also has various functions for “fast updates” of the different rendering buffers, for example if you only changed vertex positions, colors, or normals. It also supports “chunking” the mesh into multiple render buffers for faster updating, and can auto-compute tangents on mesh updates. We won’t be using any of these capabilities in this tutorial.

In terms of trade-offs, SDMC will generate larger render buffers than PMC. So, if GPU memory in your dynamic-geometry-game is a concern, it may not be the best choice. In interactive-mesh-editing contexts, this memory usage will generally pale in comparison to the many mesh copies and ancillary data structures you will need, though. SDMC also does not currently have any Physics support. And finally it cannot be serialized - you should only use SDMC in contexts where your generated mesh is saved some other way.

Runtime Geometry Architecture and ADynamicMeshBaseActor

Ok, so now we have 3 options - SMC, PMC, and SDMC. Each stores the mesh in a different way (FMeshDescription, FProcMeshSection, and FDynamicMesh3). Which one should we use? Let’s choose all of them!

The core architectural question is, where is your generated mesh coming from? If you are generating it completely procedurally, or just loading it from a file, then you can easily use any of these options, the only question is whether it’s static after being generated, frequently updated, or you want to have the convenience of not having to build sections yourself.

If you need to change the meshes after they are generated, then I strongly recommend you do not think of the mesh representation inside any of these Components as the canonical representation of your application’s data model. For starters, none of them will serialize your mesh data. And you probably have additional metadata beyond just the mesh vertices and triangles, that you would like to keep track of (and even if you don’t yet, you probably will eventually). So, I think the way you should think of the different Components is strictly as different ways to render your mesh data.

In this tutorial, “my mesh data” will be stored as FDynamicMesh3. This is a good choice if you don’t have your own mesh, in my opinion. However do know that currently there is no native serialization for FDynamicMesh3, you will need to implement that yourself. The next question is where to put this data. I am going to have it live on a C++ Actor class, ADynamicMeshBaseActor. If I were building a real app, say a mesh sculpting tool, I would probably have the mesh live in some other place, and just pass it to the ADynamicMeshBaseActor when it is modified. But for now I will have it live directly on the Actor:

UCLASS(Abstract)
class RUNTIMEGEOMETRYUTILS_API ADynamicMeshBaseActor : public AActor
{
protected:
    /** The SourceMesh used to initialize the mesh Components in the various subclasses */
    FDynamicMesh3 SourceMesh;
};

This Actor has no way to display this mesh, it needs a Component. Rather than have to make a choice, I’m going to make 3 Actor subclasses, one for each type of mesh Component:

UCLASS()
class RUNTIMEGEOMETRYUTILS_API ADynamicSMCActor : public ADynamicMeshBaseActor
{
    UPROPERTY(VisibleAnywhere)
    UStaticMeshComponent* MeshComponent = nullptr;
};

UCLASS()
class RUNTIMEGEOMETRYUTILS_API ADynamicPMCActor : public ADynamicMeshBaseActor
{
    UPROPERTY(VisibleAnywhere)
    UProceduralMeshComponent* MeshComponent = nullptr;
};

UCLASS()
class RUNTIMEGEOMETRYUTILS_API ADynamicSDMCActor : public ADynamicMeshBaseActor
{
    UPROPERTY(VisibleAnywhere)
    USimpleDynamicMeshComponent* MeshComponent = nullptr;
};

Now on the ADynamicMeshBaseActor we are going to have the following function, which has no implementation (but cannot be C++-abstract, ie = 0, because UE does not support that on UObjects):

protected:
    /**
     * Called when the SourceMesh has been modified. Subclasses override this function to 
     * update their respective Component with the new SourceMesh.
     */
    virtual void OnMeshEditedInternal();

Finally we implement this function in each of the subclasses. Essentially what each of those functions has to do, is generate and update their Component’s mesh data from the FDynamicMesh3. In the file MeshComponentRuntimeUtils.h I have added converter functions to do this, UpdateStaticMeshFromDynamicMesh() and UpdatePMCFromDynamicMesh_SplitTriangles(). The former uses the FDynamicMeshToMeshDescription class, part of GeometryProcessing, to do the conversion. For the PMC the function currently just splits each triangle. This is not the most efficient in terms of GPU memory, but is the fastest on the CPU side (in interactive mesh editing we tend to focus on the CPU side, as that’s generally the bottleneck).

For SDMC, it’s just a straight copy into the Component. Note that the SDMC does support directly editing it’s internal FDynamicMesh3. If I was cleverer, I could have allowed the base-class to access this mesh and sometimes avoid a copy. However, then I would not be using the Component-owned data as my canonical Source Mesh, which I said above was a bad idea. In some performance-sensitive situations it might make sense, but FDynamicMesh3 is very fast to copy and so just to keep things clean, I didn’t do it here.

Finally, we have one top-level API function on ADynamicMeshBaseActor that we use to actually modify the SourceMesh:

/**
 * Call EditMesh() to safely modify the SourceMesh owned by this Actor.
 * Your EditFunc will be called with the Current SourceMesh as argument,
 * and you are expected to pass back the new/modified version.
 * (If you are generating an entirely new mesh, MoveTemp can be used to do this without a copy)
 */
virtual void EditMesh(TFunctionRef<void(FDynamicMesh3&)> EditFunc);

Basically you call this function with a C++ lambda that does your actual edit. This pattern allows us to better control access to the SourceMesh, so we could in theory do things like “borrow” it from somewhere else. Another function, ::GetMeshCopy(), allows you to extract a copy of the SourceMesh from the Actor, which is needed in cases where you want to combine two meshes, for example.

And that’s basically it. If we have an instance of any of the 3 ADynamicMeshBaseActor subclasses above, we can update it in C++ by doing something like the following:

SomeMeshActor->EditMesh([&](FDynamicMesh3& MeshOut)
{
    FDynamicMesh3 NewMesh = (...);
    MeshOut = MoveTemp(NewMesh);
});

and the underlying PMC, SMC, or SDMC will be automatically updated.

One valid design question here is, why is this all done on the Actor, instead of the Component? It could of course be done on the Component too. It’s question of what you intend to do with your meshes. One complication with UE is that one Actor might have many Components, and then if you want to do things like “combine meshes”, you would have to decide how to handle these multiple, possibly hierarchical Components, some of which might not be your editable meshes. And what happens to the Actors if the Components are your primary “thing”? (These are conceptual problems we continue to struggle with in the design of the Modeling Editor Mode!!). For this tutorial I want to think of each mesh as an “object” and so organizing via Actors made sense. In addition, Actors have blueprints and this will make it easier to do fun things below.

Mesh Generation

Unfortunately our current ADynamicMeshBaseActor won’t do anything interesting in the Editor unless we initialize it in C++. So I have added some basic mesh generation functionality to it. A top-level UProperty SourceType determines whether the mesh is initialized with a generated primitive (either a box or sphere), or an imported mesh in OBJ format. The relevant sections of the Actor properties are shown below (click to enlarge). I also added the ability to control how Normals are generated, what Material is assigned to the underlying Component, and additional options for the Generation and Import. In addition there are options to enable automatic building of an AABBTree and FastWindingTree, which I will discuss below.

View fullsize

View fullsize

One note on the “Imported Mesh” option - the import path can either be a full C:\-style path, or a path relative to the project Content folder. I have included the Bunny.obj mesh with the project. This mesh will be included in the packaged build because I have added the SampleOBJFiles folder to the “Additional Non-Asset Directories to Copy” array in the Project Settings under Project - Packaging.

With these additions, we now have fully dynamic generated and imported meshes. If you open the Editor, you can find ‘Dynamic SMCActor”, as well as the PMC and SDMC actors, in the Place Actors panel (via the search box is easiest), drop one into the scene, and then change it’s parameters in the Actor DetailsView and the mesh will update, as shown in the short clip above-right.

Blueprint API

The final part of ADynamicMeshBaseActor is a small set of UFunction’s for executing mesh import/copy, spatial queries, booleans, solidification, and simplification. These are all marked BlueprintCallable and I will explain them in more detail below. But let’s look at the code for one of them, just to see what it’s like:

void ADynamicMeshBaseActor::CopyFromMesh(ADynamicMeshBaseActor* OtherMesh, bool bRecomputeNormals)
{
    // the part where we generate a new mesh
    FDynamicMesh3 TmpMesh;
    OtherMesh->GetMeshCopy(TmpMesh);

    // apply our normals setting
    if (bRecomputeNormals)
    {
        RecomputeNormals(TmpMesh);
    }

    // update the mesh
    EditMesh([&](FDynamicMesh3& MeshToUpdate)
    {
        MeshToUpdate = MoveTemp(TmpMesh);
    });
}

This is a simple function, but the point is that you can basically cut-and-paste this function, rename it, and plug any GeometryProcessing code in at “the part where we generate a new mesh”, and you’ll have access to that operation in Blueprints. The other BP API functions that apply mesh updates all do exactly that. A useful exercise would be to add the a Remesh() function by cutting-and-pasting the remeshing call from the Command-Line Geometry Processing Tutorial.

The Project

Then RuntimeGeometryDemo project has a single map, AA_RuntimeGeometryTest, with 4 “stations”. Each area does something different with runtime geometry based on the BP API I have added to ADynamicMeshBaseActor. From right-to-left we have a boolean operation, mesh simplification/solidification, spatial queries, and then another boolean demo where you get to chew away at some blocks!

The embedded video at the top of the tutorial shows a quick run-through of the different stations. We’ll walk through them in detail below.

View fullsize

Booleans!

In the first area, there are two dynamic mesh actors (both SMC in this case, but it doesn’t really matter). The red sphere is animated, and when you step on one of the three buttons on the ground labeled Union, Difference, and Intersection, that Boolean operation will be applied to these two objects, and the sphere will be deleted. The Blueprint Actor BP_ApplyBooleanButton is where the action is, and is shown below. Basically when you overlap the respective green box, it changes material, then we get both the Target and ‘Other’ Actors and call ADynamicMeshBaseActor::BooleanWithMesh(Target, Other). Then the Other Actor is Destroyed. Easy!

View fullsize

The objects for each station are grouped into a folder, shown for this part below-left. Below-right is the DetailsView properties for the above blueprint on the Button_XYZ actors. Here the various parameters in the Button BP can be configured for each Button Actor instance. Basically, you set the “Target” and “Other” Actors to two mesh actors in the current level, and pick an operation. In addition you can set the “Pressed” and “Not Pressed” materials. The SM_ButtonBox static mesh used in the BP is configured to only register Pawn overlaps, and so the ActorBeginOverlap above will only fire when the player steps on it, and kick off the Boolean operation.

View fullsize

One little BP tip, the “Validated Get” used above to only continue execution if BooleanOtherActor “Is Valid”, can be quickly created by right-clicking on a normal parameter-Get node and selecting ‘Convert to Validated Get’ at the bottom of the context menu. I only learned this after wasting countless minutes wiring up explicit IsValid branches.

Mesh Algorithms!

At the next station you can repeatedly jump or walk on/off the Simplify button to simplify the green Bunny mesh by 50% each time, or step on Solidify to run the Fast Mesh Winding Number-based remeshing. These are both essentially cut-and-pastes of the BP_ApplyBooleanButton, but they don’t take a second Actor. Below I have zoomed in on the relevant “action” section of BP_ApplySimplifyButton.

View fullsize

Spatial Queries!

The third station is not really interactive, although if you get in there and jump at just the right time, you can knock the flying sphere around. There are two objects “attached” to the semitransparent bunny. Neither are our editable mesh actors, they are just normal blueprinted StaticMeshActors, BP_MagnaSphere and BP_RotatoSphere. Their BPs are more complicated, I have shown BP_RotatoSphere below. Basically this one just moves around in a circle (“Then 0” off the Sequence node), moves a little sphere sub-Component to the nearest-point on the Bunny mesh surface (“Then 1” branch) and then changes it’s color depending on whether the StaticMesh’s location is inside or outside the Bunny (“Then 2” branch).

These latter two steps call the ContainsPoint() and DistanceToPoint() functions on the target ADynamicMeshBaseActor. These are just utility functions that query an AABBTree and FastWindingTree built for the SourceMesh automatically, if the bEnableSpatialQueries and bEnableInsideQueries UProperties are true, respectively. Otherwise they will just return false. Building these data structures can be expensive if the mesh is changing every frame, and should be disabled unless they are needed.

There is also a ADynamicMeshBaseActor::IntersectRay() function exposed to BP, which is not used in any of the examples. You might find this capability useful as runtime-generated meshes can’t necessarily be hit by LineTraces. For PMC and SMC it requires runtime physics cooking, which is not fully supported by Chaos and is generally somewhat expensive, and SDMC doesn’t support it at all. In addition ::IntersectRay() is implemented based on the double-precision DynamicMesh3/AABBTree, which can be helpful with huge meshes. (We rebuild AABBTree’s per-frame during many Modeling Mode operations in the Editor, it is not unreasonably expensive in an “editing tool” context.)

View fullsize

The BP_MagnaSphere is similar, except it uses the nearest point to add an impulse to the sphere, basically “attracting” it to the Bunny surface. This sometimes goes flying off into the world, so you might not always see it.

Shoot This!

In the final station, you can left-click to fire spheres at the red and green walls, and the spheres will be Boolean subtracted when they hit the wall. There is no physics involved here, the blueprint below detects the hits using the ADynamicMeshBaseActor::DistanceToPoint() query, between the center of the BP_Projectile actor and the wall mesh. The distance is compared to a fraction (0.25) of the radius of the projective bounding-box - this is the input to the CompareFloat node below. If it’s within range, the projectile sphere mesh is subtracted from the wall, and then destroyed. The red wall is an SDMC and the green wall is a PMC, and the projectile sphere is an SDMC, but the whole point here is it really doesn’t matter in this context.

If you recall from above, after each Subtract operation, the mesh has to be updated and the AABBTree recomputed so that the Distance to Point can be calculated. This might sound slow, but for me it generally runs at 90-100fps in PIE (run ‘stat fps’ in the console to see framerate) even if I’m shooting as fast as I can. This is surprisingly fast (I was surprised!). Turning up the tessellation level on the wall or projectile will have a noticeable effect, and it’s easy to end up getting noticeable hitches. One note, if you just hit ‘play’ and go to the wall, the pulsing red sphere at the first station will still be regenerating every frame, which slows things down (see PMC/SMC discussion above, the red sphere is an SMC). You will notice that shooting is snappier if you disable ‘Regenerate on Tick’ on the red sphere, or jump on one of the Boolean buttons first.

View fullsize

Frequent use of Get All Actors Of Class is not recommended…but it is easy!

View fullsize

Using physics for this kind of thing could be problematic because generally physics collision detection requires “simple collision” geometry, which has to be boxes spheres, capsules, or convex hulls. Decomposing the complex result of a half-blasted wall into those shapes is very difficult (read: slow). “Complex Collision” can also be used, but in that case the collision tests are much more expensive than a single distance-to-point query. A raycast could be used, and in fact I did this initially, but it meant that the ball could easily “go through” tiny holes. The distance threshold makes it “feel” much better (and can be decreased to allow each ball to do more damage). Finally it’s kind of neat to play around with the projectile mesh and/or wall mesh, like I did on the right…

Note that it would also be possible to test for exact overlaps between the two meshes here, too. TMeshAABBTree has a TestIntersection() function that takes a second TMeshAABBTree (and optional transform), and this could easily be exposed in BP, just like DistanceToPoint() is. However in this case, it would mean that the ball might not get a chance to penetrate into the wall before being subtracted (which would also be the case with complex collision). And this function is much more expensive than a simple distance query.

One final note, the BP_Projectile’s are emitted by the Fire() function on ARuntimeGeometryDemoCharacter. This could probably also be done in BP. But note that it is the only code I added to the auto-generated Third Person template project - everything else in C++ was done by the RuntimeGeometryUtils plugin.

What About Collisions?

You will notice if you run the demo that you can run right through any of the runtime-generated meshes, there is no collision. As I described above, the Boolean-gun does not use the collision system, even for line traces. Physics “cooking” is separate from rendering mesh cooking, and support for runtime physics cooking is more complicated. UProceduralMeshComponent does support runtime physics cooking, but currently only with PhysX. The situation is murkier with SMC, since the runtime Build option is very new, it’s not clear that runtime physics cooking will work (and would have the similar PhysX requirement). And SDMC does not support physics at all, as it is meant for fast visualizing during editing, and physics cooking is expensive!

However even if we do want physics, we still have a complication because as I mentioned above, “Simple Collision” is required to support physics simulation (ie things that move) and only allows for spheres, capsules, boxes, and convex hulls. So it’s necessary to approximate a complex object with a set of these simpler shapes for it to be simulated at runtime. This is essentially an unsolved problem to solve well automatically - just look at that wall above riddled with bunny-bullet-hits and imagine trying to split it up into boxes and spheres! The other option is “Complex Collision”, which is limited to static objects (ie that can be collided with but aren’t simulated) and is expensive both to cook and to test for collisions. It will do in a pinch or a prototype, but you probably don’t want to build your game around complex collision.

This is without a doubt a major thorn in the side of any game or app dependent on runtime-generated-geometry. As I have shown, it is possible to implement some physics-like effects without the full physics system. And it would be possible to implement the UPrimitiveComponent LineTrace and Overlap tests against the FDynamicMeshAABBTree, which would allow many things to “just work” (but not physics simulation). Perhaps a topic for a future article!

Late Breaking Update!

As of UE4.26 Preview 5, the default Physics system has been switched back to PhysX in the binary builds. You can still enable Chaos if you are building from source, and experiment with all the great new features that are coming in the future. However one result of this switch is Runtime Physics Cooking for the UProceduralMeshComponent is available again. So, I have added a Collision Mode field to the ADynamicMeshBaseActor, with options for Complex as Simple and Complex as Simple Async. These options will only currently have an effect on the ADynamicPMCActor, not with the SMC or SDMC. It may be possible to also get this to work with the SMC, I haven’t tried yet myself (maybe you will figure it out and submit a PR!)

The video on the right shows what happens if you switch the BP_ShootableBlock_PMC object to use either of these new modes (I also changed the material in this video, to a volumetric procedural brick texture, which is why it keeps looking like brick as it is destroyed). Since it’s not happening every frame, the physics cooking is actually quite snappy and I can’t say I noticed any real performance hit. Exciting!

A short note about the ‘Async’ variant. What this means is that the Collision cooking is done on a background thread and so it doesn’t block the game thread. This improves performance but the trade-off is that the updated collision geometry isn’t necessarily available immediately. As a result if you have quickly-changing geometry and fast-moving objects, they could more easily end up “inside” the generated meshes before the collision is finished updating.

Should you make your own Component?

This is a question that frequently comes up when looking more deeply into this problem of runtime-generated geometry. The most common case I have heard about is, you are generating meshes using an existing C++ library that has it’s own YourMeshFormat. You want to see this mesh in Unreal Engine. So as we’ve done in this tutorial, you are going to have to stuff it into a PMC or SMC to get it on the screen. This will involve one or more copies/translations of YourMeshFormat into something the Engine can ingest - either PMC Sections, an FMeshDescription, or now a FDynamicMesh3 with SDMC.

But if you dive into the PMC code, you’ll see that there is not much to the PMC and it’s SceneProxy. It won’t take you long to figure out that you could “cut out the middleman” and have a custom UYourMeshComponent that directly initializes the RenderBuffers from an instance of YourMeshFormat. In fact this is essentially what the SDMC does, where the alternative mesh format is FSimpleDynamicMesh3.

So, should you? My opinion would be, that depends on how much time you want to invest in saving a few mesh copies. If you have a large team of skilled engineers, it’s not a huge commitment, but you will have to do continual work keeping your Component up-to-date as the engine evolves. If you are a small team or indie, the small performance win may not be worth the effort. I would definitely want to profile the cost of the mesh copies/conversions, because in our experimentation, this has not been the bottleneck. Uploading the new render buffers to the GPU is still the main expense, and this doesn’t change with different Component types.

And if you organize your “mesh architecture” as I have in this tutorial, it wouldn’t necessarily matter - if you don’t depend on specific Component features, you could swap in a new Component type as needed.

(Addendum: khammassi ayoub has written a very detailed set of Medium articles about creating your own Mesh component - links here to Part 0, Part 1, and Part 2. However just a small note, much of the effort in that tutorial goes into being able to have a custom vertex shader, which is not necessary if you just want to make a “PMC but with my mesh format to avoid copies” Component. In particular you don’t need to make your own Vertex Factory/etc if you are just rendering “normal” meshes. But it’s a great read as he covers all the critical parts of Rendering-side Component/Proxy infrastructure)

Wrapping Up

That’s the end of this tutorial. I focused on Booleans here because they don’t require any parameter manipulation. However GeometryProcessing and the ModelingOperators module in the MeshModelingToolset plugin have operations like Extrusion, Offset, Bend/Twist/Taper space deformers, and more, that could easily be added to something like ADynamicMeshBaseActor and manipulated interactively in-game, with UMG or by in-world actions.

Although you could directly use ADynamicMeshBaseActor and the RuntimeGeometryUtils plugin, I really see this more of a guide for how you could build your own versions. If you are creating a game or app that involves storing content created at runtime, I would encourage you to spend some time thinking about how you want to organize this data. Storing the source meshes in the Actor was convenient for this demo, but if I were building something real, I would move ownership of those source meshes out of the Actor to some more centralized place, like a UGameInstanceSubsystem. It might seem like you can “do this later”, but if you build a lot of Blueprints on top of this current system, it will be messy to refactor later (I initially had ADynamicMeshBaseActor in the game folder, and just being able to move the .h/.cpp to the plugin without completely breaking everything involved spending an afternoon learning about Redirectors…)

It’s also not strictly necessary to have the separate PMC/SMC/SDMC Actors. Since I wanted to compare them, it was useful to split them up this way. But it would be possible to have one base actor that dynamically spawns the different Component types based on an enum. This might make life easier for working with Blueprints, as right now if you make a BP for the one of the Actor subclasses, and want to switch it to a different one, you have to jump through some hoops to change the base type, and you can’t share between multiple types (that’s why there are two shootable-wall BP’s in the tutorial, one for PMC and one for SDMC).

Finally I mentioned earlier that this will not currently work on OSX. That’s because of the USimpleDynamicMeshComponent - it is part of the MeshModelingToolset plugin, which depends on some editor-only modules that require third-party DLLs currently only available on Windows. It should be possible to get the ModelingComponents module that contains the SDMC working with some strategic #ifdef’s, but that would require recompiling the engine. A more immediate solution would be to remove ADynamicSDMCActor .h/.cpp and the “ModelingComponents” reference in the RuntimeGeometryUtils.build.cs file, and only use the SMC or PMC variants. I have verified that on Windows everything still compiles if you do this, which means it should work on OSX, but I have not tested it myself. (Note that this also breaks most of the sample project)

Thanks for reading! Don’t hesitate to post questions in the comments, or on twitter @rms80.

Command-Line Mesh Processing with Unreal Engine 4.26

This is the first of several tutorials that will (hopefully) teach you how to do advanced Mesh/Geometry Processing with Unreal Engine. Past Gradientspace Tutorials focused on the open-source Geometry3Sharp library that I developed in C#, and demonstrated how to do things like Mesh Simplification, Remeshing, Implicit Surface Modeling, and so on. G3Sharp became quite powerful, I used it to create the Cotangent 3D printing tool, and helped others use it to build Archform (a tool for designing dental aligners) and NiaFit (for designing 3D printable prosthetics). Quite a few other developers seemed to like it, too.

However, ultimately C# became a limiting factor for G3Sharp. I really like coding in C#, but the performance cost can be high, and critical math libraries like sparse linear solvers are missing from the C# ecosystem. The thought of porting even more WildMagic/GTEngine code, it was just too much! So, in December 2018 I joined Epic Games and started a C++ port of G3Sharp. Thanks to the hard work of the UE Geometry Team, this library - the GeometryProcessing plugin - has now far surpassed G3Sharp in capability. So, I think it’s about time to start showing you how to use it.

In this tutorial, I am going to walk you through a single example that generates all the meshes in the image below. In doing so, we will cover the main content of most of the previous GradientSpace G3Sharp tutorials, but in C++, in Unreal Engine. To avoid any UE complexity in this intro tutorial, we’re going to do everything in a simple command-line tool. But keep in mind that everything we’re going to do is available both in the Editor, and in-game at Runtime.

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games)

Translation for Chinese users: https://zhuanlan.zhihu.com/p/343789879

View fullsize

Preliminaries / UE4 Setup

View fullsize

Click to Enlarge

One small hurdle we have to overcome is that binary UE4 engine installations cannot build command-line executables. So, we’ll need to use the UE4 source, which you can get on Github once you have joined the Epic Games Github Organization (click link for instructions - it’s free for anyone who accepts the UE4 license agreement). This tutorial depends on code only available in version 4.26 or later, so I suggest you use the 4.26 branch (https://github.com/EpicGames/UnrealEngine/tree/4.26) directly (this tutorial should also work against the Release branch by the time you read it).

The simplest thing to do (in my opinion) is to use the Download Zip option, available under the Code drop-down button (see image to the right). Download and unzip (this will require about 1.7 GB of disk space). After that, you’ll need to run the Setup.bat file in the top-level folder, which will download another ~11GB of binary files and then run an installer that unpacks that into another ~40 GB. Unfortunately there is no more compact variant. Time for coffee!

The code for this tutorial is available on GitHub in the gradientspace UnrealMeshProcessingTools repository (click for link), in a folder named CommandLineGeometryTest in the UE4.26 samples subfolder. Again, you can download a zip of the top-level repository (click for direct link), or you can sync with a git client, too.

View fullsize

Assuming you unzipped the UE repository into a folder named “UnrealEngine-4.26”, then you’ll need to copy or move the sample code folder UE4.26\CommandLineGeometryTest to the path UnrealEngine-4.26\Engine\Source\Programs\, as shown in the image on the right. This folder contains various other command-line tools and apps that UE uses. You might be able to put it in other places, but this is where I tested it from, and where the sample HoleyBunny.obj file paths are hardcoded relative to.

For reference, I created this sample project based on the BlankProgram command-line executable that is included with the Engine (you can see it in the list on the right). This is a minimal Hello-World example program and a good starting point for any command-line executable based on UE (eg for unit testing, etc). The only modification I had to make to get things to work was to add references to several of the modules in the GeometryProcessing plugin, in the CommandLineGeometryTest.Build.cs file:

PrivateDependencyModuleNames.Add("GeometricObjects");
PrivateDependencyModuleNames.Add("DynamicMesh");

If you wanted to use these modules in other projects, you will have to do the same. Note that many parts of the Engine are not immediately available in a command-line or “Program” target type. For example in BlankProgram the UObject system is not initialized. The GeometryProcessing plugin modules have minimal engine dependencies, and do not define UObjects, so this is not a problem for this tutorial. (It is possible to initialize various engine systems, see for example the SlateViewer program.)

View fullsize

click to enlarge

Once you have the files in the right place, run the top-level GenerateProjectFiles.bat file. This will generate a Visual Studio 2019 UE4.sln file. Oh, by the way, you probably want to have Visual Studio 2019 installed, if you are on Windows. If you are on Linux or OSX, there are .command/.sh versions of the batch files I mentioned above, and this tutorial should work on those platforms, too. (GeometryProcessing has already been used in shipping games on desktop, mobile, and console platforms!!)

Open up UE4.sln, and you will find a long list of projects in the Solution Explorer subwindow. Find our CommandLineGeometryTest project, right-click on it, and select the Set as Startup Project option that appears in the context menu. Then click the Start Debugging button or hit F5. This will build for a minute or so, then pop up a command-line dialog box and print a bit of info as the tutorial runs (should only be a few seconds, though).

Note that this is not a full build of UE4. Since we are building a simple command-line app, we don’t have any dependencies on the majority of the Engine, or the Editor. A full build would take much longer - from ~15 minutes on my 24-core Threadripper to well over 2 hours on my 4-core laptop. So, make sure you don’t do a “Build Solution” or “Rebuild All”, or you are in for a long wait.

Tutorial Files

View fullsize

The sample code contains just a few files, all the code we care about is in CommandLineGeometryTest.cpp. The CommandLineGeometryTest.Build.cs and CommandLineGeometryTest.Target.cs are configuration files for the CommandLineGeometryTest UE4 module, and the CommandLineGeometryTest.h is empty.

The GeometryProcessing module does not natively support any file I/O, so the DynamicMeshOBJReader.h and DynamicMeshOBJWriter.h are necessary to read/write OBJ mesh files. The OBJ Reader is just a wrapper around the tinyobjloader library (https://github.com/tinyobjloader/tinyobjloader, source is embedded) which constructs a FDynamicMesh3 (the mesh class we will use). The OBJ Writer is minimalist, but does the basics.

CommandLineGeometryTest.cpp just contains #includes and a main() function, and I'm going to paste the entire tutorial code below. We'll step through the blocks afterwards, but I think it's instructive to skim through it all first. In less than 150 lines, this code demonstrates normals calculation, sphere and box generators, Mesh AABBTree setup and queries (nearest-point and ray-intersection), appending meshes, fast-winding-number-based resampling, implicit morphological operations, mesh simplification, isotropic remeshing, mesh hole filling, and mesh booleans (twice) ((yes, MESH BOOLEANS zomg!!)) :

// import an OBJ mesh. The path below is relative to the default path that Visual Studio will execute CommandLineGeometryTest.exe,
// when using a normal UE4.26 auto-generated UE.sln file. If things change you might need to update this path
FDynamicMesh3 ImportMesh;
FDynamicMeshOBJReader::Read("..\\..\\Source\\Programs\\CommandLineGeometryTest\\HoleyBunny.obj", ImportMesh, true, true, true);
// flip to UE orientation
ImportMesh.ReverseOrientation();

// print some mesh stats
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d vertices, %d triangles, %d edges"), ImportMesh.VertexCount(), ImportMesh.TriangleCount(), ImportMesh.EdgeCount());
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d normals"), ImportMesh.Attributes()->PrimaryNormals()->ElementCount());
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d UVs"), ImportMesh.Attributes()->PrimaryUV()->ElementCount());

// compute per-vertex normals
FMeshNormals::QuickComputeVertexNormals(ImportMesh);

// generate a small box mesh to append multiple times
FAxisAlignedBox3d ImportBounds = ImportMesh.GetBounds();
double ImportRadius = ImportBounds.DiagonalLength() * 0.5;
FMinimalBoxMeshGenerator SmallBoxGen;
SmallBoxGen.Box = FOrientedBox3d(FVector3d::Zero(), ImportRadius * 0.05 * FVector3d::One());
FDynamicMesh3 SmallBoxMesh(&SmallBoxGen.Generate());

// create a bounding-box tree, then copy the imported mesh and make an Editor for it
FDynamicMeshAABBTree3 ImportBVTree(&ImportMesh);
FDynamicMesh3 AccumMesh(ImportMesh);
FDynamicMeshEditor MeshEditor(&AccumMesh);

// append the small box mesh a bunch of times, at random-ish locations, based on a Spherical Fibonacci distribution
TSphericalFibonacci<double> PointGen(64);
for (int32 k = 0; k < PointGen.Num(); ++k)
{
    // point on a bounding sphere
    FVector3d Point = (ImportRadius * PointGen.Point(k)) + ImportBounds.Center();

    // compute the nearest point on the imported mesh
    double NearDistSqr;
    int32 NearestTriID = ImportBVTree.FindNearestTriangle(Point, NearDistSqr);
    if (ImportMesh.IsTriangle(NearestTriID) == false)
        continue;
    FDistPoint3Triangle3d DistQueryResult = TMeshQueries<FDynamicMesh3>::TriangleDistance(ImportMesh, NearestTriID, Point);

    // compute the intersection between the imported mesh and a ray from the point to the mesh center
    FRay3d RayToCenter(Point, (ImportBounds.Center() - Point).Normalized() );
    int32 HitTriID = ImportBVTree.FindNearestHitTriangle(RayToCenter);
    if (HitTriID == FDynamicMesh3::InvalidID)
        continue;
    FIntrRay3Triangle3d HitQueryResult = TMeshQueries<FDynamicMesh3>::TriangleIntersection(ImportMesh, HitTriID, RayToCenter);

    // pick the closer point
    bool bUseRayIntersection = (HitQueryResult.RayParameter < DistQueryResult.Get());
    FVector3d UsePoint = (bUseRayIntersection) ? RayToCenter.PointAt(HitQueryResult.RayParameter) : DistQueryResult.ClosestTrianglePoint;

    FVector3d TriBaryCoords = (bUseRayIntersection) ? HitQueryResult.TriangleBaryCoords : DistQueryResult.TriangleBaryCoords;
    FVector3d UseNormal = ImportMesh.GetTriBaryNormal(NearestTriID, TriBaryCoords.X, TriBaryCoords.Y, TriBaryCoords.Z);

    // position/orientation to use to append the box
    FFrame3d TriFrame(UsePoint, UseNormal);

    // append the box via the Editor
    FMeshIndexMappings TmpMappings;
    MeshEditor.AppendMesh(&SmallBoxMesh, TmpMappings,
        [TriFrame](int32 vid, const FVector3d& Vertex) { return TriFrame.FromFramePoint(Vertex); },
        [TriFrame](int32 vid, const FVector3d& Normal) { return TriFrame.FromFrameVector(Normal); });
}

// make a new AABBTree for the accumulated mesh-with-boxes
FDynamicMeshAABBTree3 AccumMeshBVTree(&AccumMesh);
// build a fast-winding-number evaluation data structure
TFastWindingTree<FDynamicMesh3> FastWinding(&AccumMeshBVTree);

// "solidify" the mesh by extracting an iso-surface of the fast-winding field, using marching cubes
// (this all happens inside TImplicitSolidify)
int32 TargetVoxelCount = 64;
double ExtendBounds = 2.0;
TImplicitSolidify<FDynamicMesh3> SolidifyCalc(&AccumMesh, &AccumMeshBVTree, &FastWinding);
SolidifyCalc.SetCellSizeAndExtendBounds(AccumMeshBVTree.GetBoundingBox(), ExtendBounds, TargetVoxelCount);
SolidifyCalc.WindingThreshold = 0.5;
SolidifyCalc.SurfaceSearchSteps = 5;
SolidifyCalc.bSolidAtBoundaries = true;
SolidifyCalc.ExtendBounds = ExtendBounds;
FDynamicMesh3 SolidMesh(&SolidifyCalc.Generate());
// position the mesh to the right of the imported mesh
MeshTransforms::Translate(SolidMesh, SolidMesh.GetBounds().Width() * FVector3d::UnitX());

// offset the solidified mesh
double OffsetDistance = ImportRadius * 0.1;
TImplicitMorphology<FDynamicMesh3> ImplicitMorphology;
ImplicitMorphology.MorphologyOp = TImplicitMorphology<FDynamicMesh3>::EMorphologyOp::Dilate;
ImplicitMorphology.Source = &SolidMesh;
FDynamicMeshAABBTree3 SolidSpatial(&SolidMesh);
ImplicitMorphology.SourceSpatial = &SolidSpatial;
ImplicitMorphology.SetCellSizesAndDistance(SolidMesh.GetCachedBounds(), OffsetDistance, 64, 64);
FDynamicMesh3 OffsetSolidMesh(&ImplicitMorphology.Generate());

// simplify the offset mesh
FDynamicMesh3 SimplifiedSolidMesh(OffsetSolidMesh);
FQEMSimplification Simplifier(&SimplifiedSolidMesh);
Simplifier.SimplifyToTriangleCount(5000);
// position to the right
MeshTransforms::Translate(SimplifiedSolidMesh, SimplifiedSolidMesh.GetBounds().Width() * FVector3d::UnitX());

// generate a sphere mesh
FSphereGenerator SphereGen;
SphereGen.Radius = ImportMesh.GetBounds().MaxDim() * 0.6;
SphereGen.NumPhi = SphereGen.NumTheta = 10;
SphereGen.bPolygroupPerQuad = true;
SphereGen.Generate();
FDynamicMesh3 SphereMesh(&SphereGen);

// generate a box mesh
FGridBoxMeshGenerator BoxGen;
BoxGen.Box = FOrientedBox3d(FVector3d::Zero(), SphereGen.Radius * FVector3d::One());
BoxGen.EdgeVertices = FIndex3i(4, 5, 6);
BoxGen.bPolygroupPerQuad = false;
BoxGen.Generate();
FDynamicMesh3 BoxMesh(&BoxGen);

// subtract the box from the sphere (the box is transformed within the FMeshBoolean)
FDynamicMesh3 BooleanResult;
FMeshBoolean DifferenceOp(
    &SphereMesh, FTransform3d::Identity(),
    &BoxMesh, FTransform3d(FQuaterniond(FVector3d::UnitY(), 45.0, true), SphereGen.Radius*FVector3d(1,-1,1)),
    &BooleanResult, FMeshBoolean::EBooleanOp::Difference);
if (DifferenceOp.Compute() == false)
{
    UE_LOG(LogBlankProgram, Display, TEXT("Boolean Failed!"));
}
FAxisAlignedBox3d BooleanBBox = BooleanResult.GetBounds();
MeshTransforms::Translate(BooleanResult, 
    (SimplifiedSolidMesh.GetBounds().Max.X + 0.6*BooleanBBox.Width())* FVector3d::UnitX() + 0.5*BooleanBBox.Height()*FVector3d::UnitZ());

// make a copy of the boolean mesh, and apply Remeshing
FDynamicMesh3 RemeshBoolMesh(BooleanResult);
RemeshBoolMesh.DiscardAttributes();
FQueueRemesher Remesher(&RemeshBoolMesh);
Remesher.SetTargetEdgeLength(ImportRadius * 0.05);
Remesher.SmoothSpeedT = 0.5;
Remesher.FastestRemesh();
MeshTransforms::Translate(RemeshBoolMesh, 1.1*RemeshBoolMesh.GetBounds().Width() * FVector3d::UnitX());

// subtract the remeshed sphere from the offset-solidified-cubesbunny
FDynamicMesh3 FinalBooleanResult;
FMeshBoolean FinalDifferenceOp(
    &SimplifiedSolidMesh, FTransform3d(-SimplifiedSolidMesh.GetBounds().Center()),
    &RemeshBoolMesh, FTransform3d( (-RemeshBoolMesh.GetBounds().Center()) + 0.5*ImportRadius*FVector3d(0.0,0,0) ),
    &FinalBooleanResult, FMeshBoolean::EBooleanOp::Intersect);
FinalDifferenceOp.Compute();

// The boolean probably has some small cracks around the border, find them and fill them
FMeshBoundaryLoops LoopsCalc(&FinalBooleanResult);
UE_LOG(LogBlankProgram, Display, TEXT("Final Boolean Mesh has %d holes"), LoopsCalc.GetLoopCount());
for (const FEdgeLoop& Loop : LoopsCalc.Loops)
{
    FMinimalHoleFiller Filler(&FinalBooleanResult, Loop);
    Filler.Fill();
}
FAxisAlignedBox3d FinalBooleanBBox = FinalBooleanResult.GetBounds();
MeshTransforms::Translate(FinalBooleanResult,
    (RemeshBoolMesh.GetBounds().Max.X + 0.6*FinalBooleanBBox.Width())*FVector3d::UnitX() + 0.5*FinalBooleanBBox.Height()*FVector3d::UnitZ() );

// write out the sequence of meshes
    FDynamicMeshOBJWriter::Write("..\\..\\Source\\Programs\\CommandLineGeometryTest\\HoleyBunny_processed.obj", 
    { AccumMesh, SolidMesh, SimplifiedSolidMesh, BooleanResult, RemeshBoolMesh, FinalBooleanResult }, true);

Import and Attributes

Ok lets step through the code. The first block just reads a mesh, prints some information, and computes normals (just a reminder, as I mentioned above, FDynamicMeshOBJReader is not part of UE4, this is a class included with the sample code). Note the call to FDynamicMesh3::ReverseOrientation(). Whether this is necessary depends on your input file, but generally, UE4 uses a left-handed coordinate system, while most content tools are right-handed. This means that a right-handed mesh, when imported into UE4, will be “inside-out”, and so (for example) the positive/outward surface normal direction for that mesh would point inwards. If we ReverseOrientation() on import, and again on export, then things will be fine.

// import an OBJ mesh. The path below is relative to the default path that Visual Studio will execute CommandLineGeometryTest.exe,
// when using a normal UE4.26 auto-generated UE.sln file. If things change you might need to update this path
FDynamicMesh3 ImportMesh;
FDynamicMeshOBJReader::Read("..\\..\\Source\\Programs\\CommandLineGeometryTest\\HoleyBunny.obj", ImportMesh, true, true, true);
// flip to UE orientation
ImportMesh.ReverseOrientation();

// print some mesh stats
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d vertices, %d triangles, %d edges"), ImportMesh.VertexCount(), ImportMesh.TriangleCount(), ImportMesh.EdgeCount());
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d normals"), ImportMesh.Attributes()->PrimaryNormals()->ElementCount());
UE_LOG(LogBlankProgram, Display, TEXT("Mesh has %d UVs"), ImportMesh.Attributes()->PrimaryUV()->ElementCount());

// compute per-vertex normals
FMeshNormals::QuickComputeVertexNormals(ImportMesh);

There is nothing special about the logging calls, I just wanted to have a reason to mention the calls to Attributes(), which return a FDynamicMeshAttributeSet. The design of FDynamicMesh3 is quite similar to DMesh3 from Geometry3Sharp, to the point where this documentation on DMesh3 basically applies directly to FDynamicMesh3. However, one major addition that has been made in the GeometryProcesing implementation is support for arbitrary Attribute Sets, including per-triangle indexed Attributes which allow for representation of things like split normals and proper UV islands/atlases/overlays (depending on your preferred terminology). Generally, mesh editing operations in GeometryProcessing (eg like the mesh edge splits/flips/collapses, the FDynamicMeshEditor, the Simplifier and Remeshers, change tracking, etc) handle updating the Attribute Sets automatically.

Generating a Box Mesh

The next step is to generate a simple box, that we are going to append to the imported bunny a bunch of times. There are a variety of mesh generators in the /Public/Generators/ subfolder in the GeometricObjects module. FMinimalBoxMeshGenerator makes a box with 12 triangles, and we’ll use FGridBoxMeshGenerator later to generate a subdivided box. The GeometricObjects module also includes a library of basic geometry and vector-math types, templated on Real type, with typedefs for float and double. So FAxisAlignedBox3d is a 3D double-precision axis-aligned bounding box, while FAxisAlignedBox2f is a 2D float variant. Conversions to the standard FVector/FBox/etc UE4 types are defined wherever possible (implicit where safe, otherwise via casts). However generally the GeometryProcessing library will calculate in double precision if not templated on Real type.

// generate a small box mesh to append multiple times
FAxisAlignedBox3d ImportBounds = ImportMesh.GetBounds();
double ImportRadius = ImportBounds.DiagonalLength() * 0.5;
FMinimalBoxMeshGenerator SmallBoxGen;
SmallBoxGen.Box = FOrientedBox3d(FVector3d::Zero(), ImportRadius * 0.05 * FVector3d::One());
FDynamicMesh3 SmallBoxMesh(&SmallBoxGen.Generate());

You will note that nearly every type is prefixed with “F”. This is a UE4 convention, generally all structs and classes have an F prefix. Similarly the code here basically follows the UE4 coding standard (which includes quite a bit more whitespace than I generally prefer, but it is what it is).

Making an AABBTree

This is a one-liner, the constructor for FDynamicMeshAABBTree3 will automatically build the AABBTree (this can be disabled with an optional argument). The AABBTree construction is quite fast and there generally is no excuse to use something less reliable (or, horror of horrors, a linear search). Similarly copying a FDynamicMesh3 is very quick, as the storage for the mesh does not involve per-element pointers, it is all in chunked arrays (see TDynamicVector) that can be memcopied. Finally this block creates a FDynamicMeshEditor, which implements a many common low-level mesh editing operations. If you need to do something it doesn’t do, it’s generally a better idea to try and break your problem down into operations that are already implemented, even at the cost of some efficiency, as handling Attribute Set updates gets quite hairy.

// create a bounding-box tree, then copy the imported mesh and make an Editor for it
FDynamicMeshAABBTree3 ImportBVTree(&ImportMesh);
FDynamicMesh3 AccumMesh(ImportMesh);
FDynamicMeshEditor MeshEditor(&AccumMesh);

If you were to look at the code for FDynamicMeshAABBTree3, you would find that it is just a typedef for TMeshAABBTree3<FDynamicMesh3>. The AABBTree is templated on mesh type, as only a few functions on the mesh are required. The FTriangleMeshAdapterd struct can be used to wrap virtually any indexed mesh in an API that will work with TMeshAABBTree3, as well as TMeshQueries<T> which supports many types of generic mesh…queries.

AABBTree Queries

This is a large block because we’re going to do a bit of logic, but the critical parts are the calls to FDynamicMeshAABBTree3::FindNearestTriangle() and FDynamicMeshAABBTree3::FindNearestHitTriangle(). These are two of the most common queries on an AABBTree. Note that in both cases, the query only returns an integer triangle ID/index, and then TMeshQueries<T> is used to execute and return a FDistPoint3Triangle3d/FIntrRay3Triangle3d object. Those classes can also be used directly. They return various information calculated for a point-triangle distance query, or ray-tri intersection. Distance and Intersection queries in GeometryProcessing are generally implemented in this style, and the calculation objects store any useful intermediate information which otherwise might be discarded. In some cases the FDistXY / FIntrXY class has static functions that will do a more minimal computation. The AABBTree class also has a ::FindNearestPoint() helper function (but no similar ray-intersection variant).

// append the small box mesh a bunch of times, at random-ish locations, based on a Spherical Fibonacci distribution
TSphericalFibonacci<double> PointGen(64);
for (int32 k = 0; k < PointGen.Num(); ++k)
{
    // point on a bounding sphere
    FVector3d Point = (ImportRadius * PointGen.Point(k)) + ImportBounds.Center();

    // compute the nearest point on the imported mesh
    double NearDistSqr;
    int32 NearestTriID = ImportBVTree.FindNearestTriangle(Point, NearDistSqr);
    if (ImportMesh.IsTriangle(NearestTriID) == false)
        continue;
    FDistPoint3Triangle3d DistQueryResult = TMeshQueries<FDynamicMesh3>::TriangleDistance(ImportMesh, NearestTriID, Point);

    // compute the intersection between the imported mesh and a ray from the point to the mesh center
    FRay3d RayToCenter(Point, (ImportBounds.Center() - Point).Normalized() );
    int32 HitTriID = ImportBVTree.FindNearestHitTriangle(RayToCenter);
    if (HitTriID == FDynamicMesh3::InvalidID)
        continue;
    FIntrRay3Triangle3d HitQueryResult = TMeshQueries<FDynamicMesh3>::TriangleIntersection(ImportMesh, HitTriID, RayToCenter);

    // pick the closer point
    bool bUseRayIntersection = (HitQueryResult.RayParameter < DistQueryResult.Get());
    FVector3d UsePoint = (bUseRayIntersection) ? RayToCenter.PointAt(HitQueryResult.RayParameter) : DistQueryResult.ClosestTrianglePoint;

    FVector3d TriBaryCoords = (bUseRayIntersection) ? HitQueryResult.TriangleBaryCoords : DistQueryResult.TriangleBaryCoords;
    FVector3d UseNormal = ImportMesh.GetTriBaryNormal(NearestTriID, TriBaryCoords.X, TriBaryCoords.Y, TriBaryCoords.Z);

    // position/orientation to use to append the box
    FFrame3d TriFrame(UsePoint, UseNormal);

    // append the box via the Editor
    FMeshIndexMappings TmpMappings;
    MeshEditor.AppendMesh(&SmallBoxMesh, TmpMappings,
        [TriFrame](int32 vid, const FVector3d& Vertex) { return TriFrame.FromFramePoint(Vertex); },
        [TriFrame](int32 vid, const FVector3d& Normal) { return TriFrame.FromFrameVector(Normal); });
}

The final call in the block above appends the SmallBoxMesh we created above, via the FDynamicMeshEditor. The two lambdas transform the vertices and normals of the box mesh (which is centered at the origin) to be aligned with the surface position and normal we calculated using the distance/ray-intersection. This is done via a FFrame3d, which is a class that is heavily used in GeometryProcessing.

A TFrame3<T> is a 3D position (referred to as the .Origin) and orientation (.Rotation), which is represented as a TQuaternion<T>, so essentially like a standard FTransform without any scaling. However the TFrame3 class has an API that allows you to treat the Frame as a set of 3D orthogonal axes positioned in space. So for example the X(), Y(), and Z() functions return the three axes. There are also various ToFrame() and FromFrame() functions (in the case of FVector3<T> you must differentiate between Point and Vector, but for other types there are overloads). ToFrame() maps geometry into the local coordinate system of the frame, so for example ToFramePoint(P) returns returns a new position that measures the distance from P to the Frame.Origin along each of it’s three axes. FromFrame() does the inverse, mapping points “in” the Frame into “world space” (as far as the Frame is concerned). So in the code above, we are treating the cube as being “in” the Frame coordinate system, and mapping it onto the mesh surface.

A final note, the FFrame3d(Point, Normal) constructor used above results in a Frame with “Z” aligned with the Normal, and somewhat arbitrary X and Y axes. In many cases you might wish to construct a Frame with specific tangent-plane axes. There is a constructor that takes X/Y/Z, but a frequent case is where you have a Normal and another direction that is not necessarily orthogonal to the Normal. In that case you can construct with Z=Normal and then use the ::ConstrainedAlignAxis() function to best-align one of the other Frame axes (eg axis X/0) with a target direction, by rotating around the Z.

“Solidification” with the Fast Mesh Winding Number

Several previous Gradientspace tutorials [1] [2] used the Fast Mesh Winding Number to reliably compute Point Containment (ie inside/outside testing) on meshes. An implementation of the Fast Mesh Winding Number is available in GeometricObjects as TFastWindingTree<T>, where T is FDynamicMesh3 or a MeshAdapter. This data structure is built on top of a TMeshAABBTree<T>. In the code below we construct one of these, and then use a TImplicitSolidify<T> object to generate a new “solidified” mesh. TImplicitSolidify interprets the inside/outside values produced by TFastWindingTree as an Implicit Surface (see previous tutorial) and uses the FMarchingCubes class to generate a triangle mesh for that implicit.

// make a new AABBTree for the accumulated mesh-with-boxes
FDynamicMeshAABBTree3 AccumMeshBVTree(&AccumMesh);
// build a fast-winding-number evaluation data structure
TFastWindingTree<FDynamicMesh3> FastWinding(&AccumMeshBVTree);

// "solidify" the mesh by extracting an iso-surface of the fast-winding field, using marching cubes
// (this all happens inside TImplicitSolidify)
int32 TargetVoxelCount = 64;
double ExtendBounds = 2.0;
TImplicitSolidify<FDynamicMesh3> SolidifyCalc(&AccumMesh, &AccumMeshBVTree, &FastWinding);
SolidifyCalc.SetCellSizeAndExtendBounds(AccumMeshBVTree.GetBoundingBox(), ExtendBounds, TargetVoxelCount);
SolidifyCalc.WindingThreshold = 0.5;
SolidifyCalc.SurfaceSearchSteps = 5;
SolidifyCalc.bSolidAtBoundaries = true;
SolidifyCalc.ExtendBounds = ExtendBounds;
FDynamicMesh3 SolidMesh(&SolidifyCalc.Generate());
// position the mesh to the right of the imported mesh
MeshTransforms::Translate(SolidMesh, SolidMesh.GetBounds().Width() * FVector3d::UnitX());

The TImplicitSolidify code is relatively straightforward, and we could have easily used FMarchingCubes here directly. However, you will find that there are many such “helper” classes like TImplicitSolidify in the GeometryProcessing modules. These classes reduce the amount of boilerplate necessary to do common mesh processing operations, making it easier to implement “recipes” and/or user interfaces that expose certain parameters.

Mesh Morphological Operations and Mesh Simplification

We’ve now generated a “solid” mesh of our holey-bunny-plus-boxes. The next step is to offset this mesh. Offset can be done directly on the mesh triangles, but it can also be considered a Morphological Operation, sometimes referred to as ‘Dilation’ (and a negative offset would be an ‘Erosion’). There are also more interesting Morphological Operations like ‘Opening’ (Erode, then Dilate) and ‘Closure’ (Dilate, then Erode), which is particularly useful for filling small holes and cavities. These are generally quite difficult to implement directly on a mesh, but easily done with implicit surface / level-set techniques in the TImplicitMorphology<T> class. Similar to TImplicitSolidify, this class builds the necessary data structures and uses FMarchingCubes to generate an output mesh.

// offset the solidified mesh
double OffsetDistance = ImportRadius * 0.1;
TImplicitMorphology<FDynamicMesh3> ImplicitMorphology;
ImplicitMorphology.MorphologyOp = TImplicitMorphology<FDynamicMesh3>::EMorphologyOp::Dilate;
ImplicitMorphology.Source = &SolidMesh;
FDynamicMeshAABBTree3 SolidSpatial(&SolidMesh);
ImplicitMorphology.SourceSpatial = &SolidSpatial;
ImplicitMorphology.SetCellSizesAndDistance(SolidMesh.GetCachedBounds(), OffsetDistance, 64, 64);
FDynamicMesh3 OffsetSolidMesh(&ImplicitMorphology.Generate());

// simplify the offset mesh
FDynamicMesh3 SimplifiedSolidMesh(OffsetSolidMesh);
FQEMSimplification Simplifier(&SimplifiedSolidMesh);
Simplifier.SimplifyToTriangleCount(5000);
// position to the right
MeshTransforms::Translate(SimplifiedSolidMesh, SimplifiedSolidMesh.GetBounds().Width() * FVector3d::UnitX());

Marching Cubes meshes are generally very dense, and so it’s a common pattern to Simplify the mesh afterwards. This can be done in a few lines using the FQEMSimplification class, which has a variety of simplification criteria you can specify. There are also several other Simplifier implementations, in particular FAttrMeshSimplification will consider the normal and UV Attribute Overlays.

Mesh Booleans (!!!)

It’s the moment you’ve been waiting for - Mesh Booleans! In this block we first use FSphereGenerator and FGridBoxGenerator to generate two meshes, and then use FMeshBoolean to subtract the Box from the Sphere. The FMeshBoolean constructor takes a transform for each input mesh, but only supports two input meshes (ie it’s not an N-way Boolean). If you would like to use multiple input meshes, you will have to use repeated FMeshBoolean operations, but if the inputs are not intersecting it can be more efficient to combine them using FDynamicMeshEditor::AppendMesh() first.

// generate a sphere mesh
FSphereGenerator SphereGen;
SphereGen.Radius = ImportMesh.GetBounds().MaxDim() * 0.6;
SphereGen.NumPhi = SphereGen.NumTheta = 10;
SphereGen.bPolygroupPerQuad = true;
SphereGen.Generate();
FDynamicMesh3 SphereMesh(&SphereGen);

// generate a box mesh
FGridBoxMeshGenerator BoxGen;
BoxGen.Box = FOrientedBox3d(FVector3d::Zero(), SphereGen.Radius * FVector3d::One());
BoxGen.EdgeVertices = FIndex3i(4, 5, 6);
BoxGen.bPolygroupPerQuad = false;
BoxGen.Generate();
FDynamicMesh3 BoxMesh(&BoxGen);

// subtract the box from the sphere (the box is transformed within the FMeshBoolean)
FDynamicMesh3 BooleanResult;
FMeshBoolean DifferenceOp(
    &SphereMesh, FTransform3d::Identity(),
    &BoxMesh, FTransform3d(FQuaterniond(FVector3d::UnitY(), 45.0, true), SphereGen.Radius*FVector3d(1,-1,1)),
    &BooleanResult, FMeshBoolean::EBooleanOp::Difference);
if (DifferenceOp.Compute() == false)
{
    UE_LOG(LogGeometryTest, Display, TEXT("Boolean Failed!"));
}
FAxisAlignedBox3d BooleanBBox = BooleanResult.GetBounds();
MeshTransforms::Translate(BooleanResult, 
    (SimplifiedSolidMesh.GetBounds().Max.X + 0.6*BooleanBBox.Width())* FVector3d::UnitX() + 0.5*BooleanBBox.Height()*FVector3d::UnitZ());

Note that the MeshBoolean is not 100% reliable. Below I will show how to (try to) handle failures.

Remeshing

Next we apply a pass of isotropic triangular remeshing to the Boolean result. This is a standard step if you are planning on doing further mesh processing like deformations/smoothing/etc, as output of a Mesh Boolean often has highly variable triangle size/density (which constraints how the mesh can move) and sliver triangles that can cause numerical issues. The standard approach is to use FRemesher and run a fixed number of passes over the full mesh. Below I used FQueueRemesher, which produces nearly the same result, but rather than full-mesh passes, an “active queue” of meshes that need to be processed is tracked. This can be significantly faster (particularly on large meshes).

// make a copy of the boolean mesh, and apply Remeshing
FDynamicMesh3 RemeshBoolMesh(BooleanResult);
RemeshBoolMesh.DiscardAttributes();
FQueueRemesher Remesher(&RemeshBoolMesh);
Remesher.SetTargetEdgeLength(ImportRadius * 0.05);
Remesher.SmoothSpeedT = 0.5;
Remesher.FastestRemesh();
MeshTransforms::Translate(RemeshBoolMesh, 1.1*RemeshBoolMesh.GetBounds().Width() * FVector3d::UnitX());

I covered the basics of Isotropic Remeshing in a previous G3Sharp tutorial. That tutorial basically applies directly to the UE4 GeometryProcessing implementation, down to the type and field names (don’t forget to add F). However the UE4 version is quite a bit more capable, for example the FQueueRemesher is much faster, and there is also FSubRegionRemesher which can remesh a portion of a larger mesh.

Two notes about the block above. First, I did not use a Projection Target (described in the linked tutorial), so the nice crisp edges of the sphere-minus-cube will be smoothed away. Setting up a Projection Target only takes a few lines, search for any usage of FMeshProjectionTarget in the Engine code. Second, the first thing I did after making the mesh copy above is to call RemeshBoolMesh.DiscardAttributes(). This call removes all attribute overlays from the mesh, specifically the per-triangle the UV and Normal layers. The Remeshers do support remeshing with per-triangle attributes, however it is more complex because those attributes have additional topological constraints that must be preserved. The utility function FMeshConstraintsUtil::ConstrainAllBoundariesAndSeams() can be used to more-or-less automatically set all that up, but even just calling that is a bit complicated, so I thought I would save it for a future tutorial (look up FRemeshMeshOp if you want to see an example).

Hole Filling and Boolean Failure Handling

View fullsize

Finally, we are going to compute the Boolean Intersection of the smoothed-out-sphere-minus-cube with the solidified-offset-cubesbunny. This is again just a single construction of a FMeshBoolean object and a call to Compute(). However, in this case the input objects are quite complex and it’s relatively likely that the Mesh Boolean output is not fully closed.

Why? Well, Mesh Booleans are notoriously difficult to compute reliably. If you have used tools like Maya or Max over many years, you will recall that Mesh Booleans used to be extremely unreliable, and then at some points they switched to being somewhat more reliable. This is mainly due to those packages changing which third-party Mesh Boolean library they were using. There actually aren’t that many to choose from. The CGAL library has quite powerful Polyhedral Booleans, but they are very, very slow, and cannot be redistributed with a commercial game engine. Carve is used by Blender, and is quite good, but it is GPL-licensed. Cork is reasonably capable but not actively maintained. The Mesh Booleans in LibIGL use the recently-introduced Mesh Arrangements technique and are basically the current state-of-the-art, but are also somewhat slow on large meshes, and depend on some CGAL code. If you dig, you will find that the Booleans available in many commercial tools or open-source libraries are using one of these four.

Another complication with third-party mesh boolean libraries is they generally don’t support arbitrary complex mesh atttributes, like the indexed per-triangle overlays I mentioned above. So, in UE4.26 we wrote our own. One benefit to writing an implementation specifically for FDynamicMesh3 is that we could take advantage of some modern triangle-mesh-processing techniques. For example when previous Mesh Booleans failed catastrophically, ie with parts of the output disappearing, it was often because they couldn’t geometrically tell what was “inside” and “outside”. Now that we have the Fast Mesh Winding Number, this is basically a solved problem, and as a result UE4’s FMeshBoolean tends to fail in a way that is localized, and often recoverable. For example in the images above-right, the sphere mesh has a giant hole in it, usually a no-go for a Mesh Boolean, but as long as the intersection curve is well-defined, FMeshBoolean will usually work. Even if it does (lower image), the Boolean no longer really makes sense, but the failure is not catastrophic, we just get a hole where the hole is.

So, all of that is a long-winded way of saying that if your FMeshBoolean::Compute() returns false, it’s probably got some holes and you can fill them. The FMeshBoundaryLoops object will extract a set of FEdgeLoop objects that represent the open boundary loops of a mesh (another surprisingly difficult problem…) and then FMinimalHoleFiller will fill them (we also have FPlanarHoleFiller and FSmoothHoleFiller but they likely aren’t applicable in this context). Note that most of the “holes” are zero-area cracks along the intersection curve between the two objects, so it can be helpful to collapse away degenerate triangles (something the library does not do automatically, yet).

// subtract the remeshed sphere from the offset-solidified-cubesbunny
FDynamicMesh3 FinalBooleanResult;
FMeshBoolean FinalDifferenceOp(
    &SimplifiedSolidMesh, FTransform3d(-SimplifiedSolidMesh.GetBounds().Center()),
    &RemeshBoolMesh, FTransform3d( (-RemeshBoolMesh.GetBounds().Center()) + 0.5*ImportRadius*FVector3d(0.0,0,0) ),
    &FinalBooleanResult, FMeshBoolean::EBooleanOp::Intersect);
FinalDifferenceOp.Compute();

// The boolean probably has some small cracks around the border, find them and fill them
FMeshBoundaryLoops LoopsCalc(&FinalBooleanResult);
UE_LOG(LogGeometryTest, Display, TEXT("Final Boolean Mesh has %d holes"), LoopsCalc.GetLoopCount());
for (const FEdgeLoop& Loop : LoopsCalc.Loops)
{
    FMinimalHoleFiller Filler(&FinalBooleanResult, Loop);
    Filler.Fill();
}
FAxisAlignedBox3d FinalBooleanBBox = FinalBooleanResult.GetBounds();
MeshTransforms::Translate(FinalBooleanResult,
    (RemeshBoolMesh.GetBounds().Max.X + 0.6*FinalBooleanBBox.Width())*FVector3d::UnitX() + 0.5*FinalBooleanBBox.Height()*FVector3d::UnitZ() );

The GeometryProcessing Library

The examples above have shown you how to use a handful of the data structures and algorithms in the GeometryProcessing Plugin. There are many, many more, and even the ones used above have many more options and capabilities. You will find all the code in \Engine\Plugins\Experimental\GeometryProcessing\, there are four modules:

• GeometryObjects: templated vector-math and geometry types, Distance and Intersection computations, spatial data structures like AABBTrees/Octrees/Grids/HashTables, and Grids, Mesh Generators, 2D graphs and polygons, generic mesh algorithms (not specific to FDynamicMesh3), and Implicit Surfaces

• DynamicMesh: FDynamicMesh3 and related data structures, booleans and cutting, editing operations like extrusions and offsets, deformation, sampling, parameterization, baking, shape fitting, and so on. Nearly all the Mesh Processing code is here

• GeometryAlgorithms: Computational-Geometry algorithm implementations like Delaunay Triangulation, Convex Hulls, Line Segment Arrangement, and so on. This module uses the third-party boost-licensed GTEngine library in some places (included in /Private/ThirdParty/) and also Shewchuck’s Exact Predicates.

• MeshConversion: Helper classes for converting between mesh types. Currently main for converting to/from FMeshDescription, the other main mesh format used in Unreal Engine.

I encourage you to explore. If you find a class or function that looks interesting but aren’t sure exactly how to use it, you will almost certainly find some usage elsewhere in the Engine codebase. One great thing about Unreal Engine is you have the code for literally everything, including the Editor. So if you see something interesting when using the Modeling Tools Editor Mode, and want to know how to do it yourself, you can find the code in the MeshModelingToolset plugin. This is built on top of GeometryProcessing and implements nearly all the interactive in-Editor Tools.

Many of those Tools (particularly the ones that are more “set options and process” and less “pointy-clicky”) are split into the Tool-level code (in the MeshModelingTools module) and what we call an “Operator” (in the ModelingOperators module). An Operator is basically an object that executes a more complex multi-step mesh processing recipe, with higher-level parameters exposed. So for example the FBooleanMeshesOp operator ultimately runs a FMeshBoolean on two input FDynamicMesh3, however it will automatically do the hole-filling repair step above if bAttemptFixHoles is set to true. Operators are safe to run on background threads, and take a FProgressCancel object, which can be used to safely abort their computation if they take too long.

Create your own In-Editor Geometry Processing Tools

This tutorial has shown you how to use the GeometryProcessing modules in a a command-line tool. However, as I mentioned above, this plugin can be used to implement the same mesh processing in the Editor. My previous tutorial on using LibIGL in UE 4.24 to make an interactive mesh smoothing tool in the Editor already showed how to do this!! That tutorial ultimately reduced the problem to implementing a MakeMeshProcessingFunction() function that returned a TUniqueFunction<void(FDynamicMesh3&)>, ie a lambda that processed the input FDynamicMesh3. In that tutorial we wanted to call LibIGL code so we converted to/from the LibIGL mesh format. But now you know that you can also just skip LibIGL and edit the input mesh using GeometryProcessing code directly!

I have updated that tutorial for UE 4.26, there is a small addendum explaining the necessary changes. In UE 4.26 we added a new “base tool” class UBaseGeometryProcessingTool which makes the code for that tutorial much simpler.

As I mentioned, the GeometryProcessing Plugin is made up of Runtime modules, so there is nothing stopping you from using it in your games, either. I will be exploring this in future tutorials - stay tuned!

Interactive Mesh Processing with libigl in Unreal Engine 4.24

The code for this tutorial has been updated for UE 4.26 - see the update notes below!

View fullsize

This tutorial describes how to embed libigl triangle mesh processing code inside an Interactive Tool in the Unreal Editor. Interactive Tools are an Experimental feature in UE 4.24, meaning they are not documented or officially supported. However this doesn’t mean they aren’t useful! Using the sample project below, you will be able to select a StaticMesh Actor/Component in the scene, and then start a Tool that applies Laplacian Mesh Smoothing to the underlying StaticMesh Asset. The smoothing parameters (ie sliders, checkboxes, etc) are automatically exposed in a DetailsView panel. The gif to the right shows a quick demo of applying this smoothing to one of the chairs in the default UE scene.

(Of course the point of this tutorial is not just to provide a mesh smoothing Tool, it’s to show you how to create your own Tools inside the Editor. Libigl is just a convenient (and awesome) example.)

(Mandatory Disclaimer: your author, Ryan Schmidt, is an employee of Epic Games)

What is libigl? Why would I want to do this?

Libigl (https://libigl.github.io/) is an open-source C++ mesh processing library (github) initially created by two computer graphics PhD students (now professors) Alec Jacobson (UToronto) and Danielle Panozzo (NYU). If you see a cool SIGGRAPH paper that does something crazy with meshes, there is a good chance it is based on libigl. For example, Alec and his student Derek Liu had a paper Cubic Stylization at SIGGRAPH Asia 2019 that was reviewed on the popular 2-Minute Papers youtube channel (click here to watch). Their code is open-source (github) and built on top of libigl.

So, if you wanted to Cubic-Stylize some of your game assets, you could try to download and compile their software and run it on your objects. However as research software, it’s UI has…limitations (your assets are all OBJ files, right?). If you could get this code running in the Editor as an Interactive Tool, you could apply it to your already-created-and-configured Unreal Assets.

Did I mention that libigl has an enormous tutorial that demonstrates a ton of amazing geometry processing algorithms, with sample code easily cut-and-pasteable? In fact the mesh smoothing in the gif above is just the 205_Laplacian sample code [link] and the purpose of this tutorial is to get you as close as possible to literally being able to cut-and-paste libigl-based code into an Editor Tool.

(By the way, libigl is not the only C++ mesh processing library out there, and the plugin provided as part of this tutorial should be adaptable to any of those, too - details later on.)

UE 4.24 Sample Project & MeshProcessingPlugin

This is the tab for the Mesh Processing Mode

The Tool Buttons will activate when a valid object is selected

You must Accept the active Tool to commit the current preview to the underlying StaticMesh asset

To make it trivial to use libigl inside of UE, I have written a small plugin that provides two things. First, it’s an Editor Mode plugin, which means it adds its own tab in the Editor Modes tab panel on the left-hand side of the Editor. The tab for this mode will have a default “Wrench-Brush-Pencil” icon (see images to right).

When you select this new mode, a small toolbar of buttons will appear below the main toolbar. It will contain two buttons labeled IGLSmooth and Export. You have to select a StaticMesh object in the viewport to start these Tools. The Export Tool will allow you to export the selected mesh as an OBJ file, but I won’t cover this in more detail in the tutorial.

When you start a tool, two additional buttons will appear, labeled Accept and Cancel. A tool is like a mini-mode with a live preview, so what you see in the chair-smoothing gif above is not actually affecting the input StaticMesh Asset yet. Selecting Accept will commit the current preview to the Asset (or Cancel to discard it). Note that clicking Accept edits the Asset but does not save it! You must save the Asset manually (eg Save-All from the File menu, select the Asset and click Save, etc, etc)

And that’s it. This sample project is on Github at github.com/gradientspace/UnrealMeshProcessingTools in the UE4.24 subfolder. The project itself is just an empty default Game C++ project, all the actual code is in the Editor Mode Plugin located in the subdirectory /Plugins/MeshProcessingPlugin/. You should be able to copy that Plugin to another UE 4.24 Project without difficulty, if you prefer.

Note that the Plugin contains copies of libigl and Eigen (an awesome header-only math library that libigl is built on). If you want to use your own copies of these at some other system path, you can edit the quoted strings in Plugins/MeshProcessingPlugin/Source/MeshProcessingPlugin/MeshProcessingPlugin.Build.cs (you can use absolute paths).

Details on how to install UE4.24 and import this sample project are provided below, if you need it. But lets cover the libigl-related parts first.

IGLSmoothingTool Code

The code you need to care about for this tutorial is located in /Plugins/MeshProcessingPlugin/Source/MeshProcessingPlugin/Public/Tools/IGLSmoothingTool.h and Private/Tools/IGLSmoothingTool.cpp. There are roughly 40 lines of non-whitespace/comment code between these two files, so there really is not much to it beyond the actual libigl code. I’ll describe all the salient parts. It will feel a bit like magic that this works. Don’t worry about it - that’s the whole point of the Editor Tools Framework! There are 3 objects we have to provide for the magic to happen - a ToolBuilder, and PropertySet, and the Tool itself:

The ToolBuilder

UIGLSmoothingToolBuilder is a trivial factory class that creates instances of UIGLSmoothingTool. The ToolBuilder code should be straightfoward, it’s just allocating a new object using NewObject<T>, which is an Unrealism for creating new UObject-derived subclasses (many things in Unreal are UObjects). If this is your first exposure to Unreal Engine you might note that all classes/structs are prefixed with U or F. U means UObject, F is everything-else (just go with it for now). Similarly just ignore the UCLASS() and GENERATED_BODY() macros. Unreal has a custom pre-processor/code-generator that parses these macros, so they have to be there.

The PropertySet

Next is UIGLSmoothingToolProperties. This is a UInteractiveToolPropertySet implementation, which means it provides a list of configuration variables that will appear in the properties panel on the left-hand side of the Editor when the Tool is active. When you change a property the Tool will recompute the preview. The properties have to be annotated with UPROPERTY() macros but again you can cut-paste what is there if you wanted to add more (only certain types are supported though - stick to int/float/boolean, and enums if you need it, see the MeshExportTool.h header for an example). Note that as long as you initialize the values in the header you don’t need anything for this class in the cpp file.

The Tool

Finally we have UIGLSmoothingTool. The header declaration of this class isn’t really important, if you want to change the libigl code all that matters is the implementation of the ::MakeMeshProcessingFunction() function. I have included the code for this function below (slightly edited to compact it vertically).

The basic task of this function is to create and return a lambda that updates the input FDynamicMesh3 (our editable Unreal mesh). To do that with libigl we will first have to convert the mesh vertices and triangles to matrix format. The rest of the code is taken from libigl sample Laplacian_205 (github), lightly edited to remove the origin scaling/translation in that sample (otherwise we would need to invert that transformation).

TUniqueFunction<void(FDynamicMesh3&)> UIGLSmoothingTool::MakeMeshProcessingFunction()
{
    // make local copies of current settings
    int SolveIterations = Properties->Iterations;
    float Smoothness = Properties->Smoothness;

    // construct compute lambda
    auto EditFunction = [Smoothness, SolveIterations](FDynamicMesh3& ResultMesh)
    {
        Eigen::MatrixXd V;      Eigen::MatrixXi F;    
        iglext::DynamicMeshToIGLMesh(ResultMesh, V, F);    // convert FDynamicMesh3 to igl mesh representation

        Eigen::SparseMatrix<double> L;
        igl::cotmatrix(V, F, L);    // Compute Laplace-Beltrami operator L

        Eigen::MatrixXd U = V;      // smoothed positions will be computed in U

        for (int k = 0; k < SolveIterations; ++k)
        {
            Eigen::SparseMatrix<double> M;     // Recompute mass matrix on each step
            igl::massmatrix(U, F, igl::MASSMATRIX_TYPE_BARYCENTRIC, M);

            const auto& S = (M - Smoothness * L);
            Eigen::SimplicialLLT<Eigen::SparseMatrix<double>> solver(S);
            U = solver.solve(M * U).eval();    // Solve (M-delta*L) U = M*U
        }
        
        iglext::SetVertexPositions(ResultMesh, U);   // copy updated positions back to FDynamicMesh3
    };

    return MoveTemp(EditFunction);  // return compute lambda
}

The conversion between the FDynamicMesh3 and the libigl V/F mesh format is done by utility code in /Tools/IGLUtil.h. If you want to use some other mesh library, you will need to write similar converters. FDynamicMesh3 supports many capabilities not available in most open-source mesh libraries, such as split normals, multiple layers of UV maps, deleting vertices and triangles, etc. This class is a ported and evolved version of the DMesh3 format from the geometry3Sharp library, which I documented here, if you are interested in using it directly.

Note also that the local copies of the configuration settings SolveIterations and Smoothness are pretty important (see extended comments in the github cpp). The lambda we return here (TUniqueFunction is an Unreal version of std::function) will be called from a different thread. So we cannot reference the Properties object directly.

Note also that multiple instances of the lambda may execute simultaneously, as the Tool framework will spawns new computations when the user edits settings, rather than wait for the previous one to finish. If your code is going to depend on global variables/etc, you will need to use a lock. Unreal’s FCriticalSection is an easy way to do this (please post in the comments if you would like me to add instructions on doing this, or handle it in the parent MeshProcessingTool).

That’s it! (p.s. Live Coding)

You now know everything you need to do to write libigl code that will be run inside an Interactive Tool in the Unreal Editor. That’s really all there is to it. You can edit the libigl code in Visual Studio, hit Play to recompile and launch the Editor, and try out your changes. This is the development loop for Unreal Engine.

….except, Unreal Engine also supports hot reloading of C++. This feature is called Live Coding and it will let you iterate much more quickly. Live Coding is not enabled by default, but if you click on the Compile drop-down arrow in the main toolbar, you can toggle on Enable Live Coding (see image to the right).

Then you just hit Ctrl+Alt+F11 in the Unreal Editor to recompile and patch the currently-running Editor. The Live Coding Log Window will show compiler output and/or errors. Note that some changes cannot be made with Live Coding. In particular, you cannot add/edit UPROPERTY() fields in the Properties object - changes to those require a restart. (In this context I do recommend Cancelling out of the Tool before doing the hot-reload, otherwise you might get crashes when you Cancel later).

Detailed Setup Instructions

The instructions above explain how to do the libigl part of this tutorial. However if you are new to UE4, it might not be obvious how to get to the point where you will be able to edit that block of libigl code. So, this section will walk you through it step by step.

Step 0 - Pre-requisites

To do anything with Unreal Engine you will need to have a C++ development environment set up. Currently this tutorial only works on Windows, so you will need to install Visual Studio - I used Visual Studio Community 2019 which is free and can be downloaded here.

You also need to get the sample project from Github, at https://github.com/gradientspace/UnrealMeshProcessingTools. The simplest way to get the project is to just download a zip of the repository, which you can do by clicking here. Alternately you can clone out and/or fork the repository - you’ll have to find instructions on doing that elsewhere, though.

Between Visual Studio and Unreal Engine you will probably need about 30 GB of free disk space. If you are hurting for space, you should be able to customize the configuration of each to get it down to maybe 15GB total.

Step 1 - Install Unreal Engine version 4.24.x

You will need to have installed Unreal Engine 4.24 to use this tutorial. Go to https://www.unrealengine.com and click the Download button in the top-right. You will have to sign up for an Epic Games account, then download and run the Epic Games Launcher, and sign in to the launcher with that account.

Once you have done that, follow the instructions to the right to install Unreal Engine. Click the thumbnails on the bottom to see instructions for the various steps in the image captions. You can save some disk space by disabling support for the various platforms (Android, iOS, etc), as we’re only using the Editor. But don’t disable the Starter Content Packs, or you won’t have anything in the scene to work with.

I also strongly recommend that you check the box to include the full Engine/Editor source (not shown in the images). Being able to look at the Engine source can be extremely useful both for debugging and just for seeing “how things are done” when you want to do something similar. Entrian Source Search is quite good for this kind of Engine code spelunking.

Browse to the Unreal Engine tab on the left, and then the Library tab on the top bar. Click the + button to add a new engine version.

Select a version of UE 4.24 and click the Install button

Click through the EULA and then choose an install location (the default works fine). You can save some disk space by going into Options and disabling all the optional platforms. Then click Install and get a coffee.

Click the More button to get to a different dialog where you can open an existing project

On this screen click the Browse button to pop up a file browser

Browse to wherever you have your local copy of the project, select the IGLMeshProcessing.uproject file, and click Open

This dialog will pop up. Click Yes. A progress bar will appear for a while, and after that the UE Editor will open.

Once the compile finishes, Unreal Editor will launch. The Modes Tabs are in the top-left and the highlighted button will get you into the Mesh Processing Mode

Open the File menu and click on Generate Visual Studio Project

Click on the File menu again and select Open Visual Studio to launch Visual Studio with the generated project file

Step 2 - Open The Sample Project

Once you have installed Unreal Engine, the greyed-out Launch button in the top-right of the Epic Launcher will turn orange. Click that button to start the Unreal Editor. The first screen you see will be the one on the right, to Select or Create New Project. Follow the instructions in the images. You will open and compile the project you downloaded from Github, and then the Editor will launch with that project.

Once the Editor launches you can run the IGL Smooth Tool described above, by switching to the Mesh Processing Editor Mode. To get to the C++ code, you will need to first run Generate Visual Studio Project from the File menu, then Open Visual Studio, again from the File menu, to launch VS with the project code open.

Once you have launched Visual Studio, close the instance of the Unreal Editor that you already opened. When you are working with the C++ code it is likely that you will need to relaunch the Editor frequently (eg after code changes…or crashes), and also use the debugger, and this is all much smoother if launching from Visual Studio.

Step 3 - Working in Visual Studio

View fullsize

The image to the right shows the expanded code tree for the IGLMeshProcessing plugin in Visual Studio (click to enlarge it). /Plugins/ is the top-level plugins directory, below that /MeshProcessingPlugin/ is our plugin, then /Source/ is where the source code modules are, and then we have another /MeshProcessingPlugin/ folder, this is the Module and probably should have been named differently (my mistake). A Plugin is a collection of Modules, and each Module will become a separate DLL (Modules link to other Modules, Plugins are just an organizational structure).

Finally we have the /Private/ and /Public/ folders. Generally headers containing types we may need to export (in the DLL) go in /Public/ and everything else goes in /Private/. The IGLSmoothingTool code is in the /Tools/ subdirectory. We could (should?) have put the actual Tools code in a separate Module from our Editor Mode but that would complicate this sample project.

Click the Start Debugging button in Visual Studio (green triangle in the top toolbar) to launch the Editor with the IGLMeshProcessing project.

If you want to add additional Tools, the simplest thing to do is just duplicate the IGLSmoothingTool.h and .cpp, and string-replace “IGLSmoothing” with something else. If you do this, you may also need to manually “Regenerate Project Files”. You can do this by right-clicking on the IGLMeshProcessing.uproject file and selecting Generate Visual Studio project files. Visual Studio will prompt you to reload the solution, click Yes to All.

Step 4 - Import, Export, and Assets

to import a mesh file (FBX or OBJ) as a StaticMesh asset, right-click in the Content Browser and select Import To /Game

For OBJ files, configure the FBX Import options as shown here

Your mesh file will be imported as a new StaticMesh Asset in the Content Browser

Drag-and-drop the Mesh Asset into the scene. Your bunny appears!

At this point you can edit the code, run the project, and apply your libigl code to the default meshes in the scene. If you want to import other objects, you will need to know a tiny bit about the UE4 Asset system. UE4 does not have a “scene file” that contains mesh data, like you might have in Maya or Blender. In UE4 every mesh is a separate “Asset” with is stored in a .uasset file.

To Import a mesh file (OBJ, FBX, and a few other formats) as an asset, right-click in the Content Browser (the part on the bottom) and select Import to /Game. Select your file and then the FBX Import Options dialog will pop up (the FBX importer is used for OBJ files too). For “geometry processing” meshes, I recommend disabling creating of Materials. You should also un-check Remove Degenerates, or small triangles will be deleted on import (yes this is really the default). Also check Combine Meshes unless you are sure you want multiple objects (any ‘g’ or ‘o’ lines in an OBJ file will result in a separate mesh asset). Finally click Import All. If you were to do this with this bunny OBJ file (click), you would end up with a StaticMesh Asset named UEBunny. You can then drag-and-drop that mesh into the scene.

Click through to the last image on the right, and you will see a star indicator ( ☆ ) on the imported UEBunny Asset icon. This means the Asset is in the modified-but-unsaved state. Assets are saved separately from the actual scene in UE, and an imported Asset is not explicitly saved. You must either Save All (Ctrl+Shift+S) or select the Asset itself and hit Ctrl+S to Save (or use Save from the context menu). When you do this, you create a new file UEBunny.uasset in the top-level Content folder. Similarly when you edit the Asset with the IGL Smooth Tool, it will be modified but unsaved. If you shut down the Editor, you will be prompted to save any modified-but-unsaved Assets. You can skip this if you don’t want to save it. In any case, your imported mesh will not be modified or affected by what you do inside Unreal, because you are working with the Asset file, not the OBJ/FBX/etc (which is called the “Source File” in UE terminology).

Note that you can easily Re-import an external mesh by right-clicking on the Asset and selecting Reimport. Unreal remembers the import settings in the uasset file. If your mesh doesn’t import correctly (for example if there are “cracks”) you might try some of the mesh repair tools in Modeling Mode (see below).

You can Export a StaticMesh Asset by right-clicking on it and selecting Asset Actions and then Export. FBX and OBJ format are supported, however the OBJ exporter exports each triangle separately (ie more like an STL file). For your Geometry Processing experiments you might want that connectivity. In that case, use the Export button in the Mesh Processing Editor Mode, which will allow you to export an OBJ file using the MeshExportTool I have provided.

Finally, note that Unreal uses a left-handed Z-Up coordinate system (more details here). It’s unlikely that you are using this same system (it is a bit unusual outside of game engines). For example Maya and Meshmixer use right-handed Y-Up, while Blender and 3DS Max use right-handed Z-Up. The FBX Importer will convert OBJ format from right-to-left handed (and FBX specifies handedness in the file) but will not modify the Up direction. The Mesh Export Tool defaults will export right-handed Y-Up suitable for use in Maya and Meshmixer (my preferred external tools), but you can change the options.

Finally Finally, the default units in Unreal are centimeters. So an object on the scale of a unit-box (ie good for algorithms) will be tiny compared to the default ground-plane-box (which is 5 meters wide). Also note that if you scale an object in the 3D viewport using the 3D gizmo, that’s just modifying a Transform on the StaticMeshComponent, not the actual local coordinates of the mesh vertices in the Asset.

MeshProcessingPlugin Details

IGLSmoothingTool is the “end-goal” for the MeshProcessingPlugin, allowing you to write a tiny bit of libigl code that will drive a relatively complex underlying system. Much of that system is part of UE 4.24, however a few parts were written specifically for this tutorial. If you want to know how they work, here are some details (and if you don’t - skip this section!)

MeshProcessingTool

The UIGLSmoothingTool class shown above is based on a parent Tool implementation called UMeshProcessingTool. This Tool provides the “glue” that allows our libigl code to manipulate a UE4 StaticMesh Asset without really having to know anything about UE4. This interface is provided by way of the Interactive Tools Framework. UMeshProcessingTool implements UInteractiveTool (by way of USingleSelectionTool), which is the base interface for Interactive Tools in the Framework. You can think of an Interactive Tool as a “mini-mode” in the Editor - when a Tool is active it is Ticked each frame, has the opportunity to do things like debug line drawing in it’s Render function, provides sets of editable properties that are shown in the Mode Panel, and can do things like handle mouse input or create 3D gizmos (we aren’t using those capabilities in this tutorial, though).

UMeshProcessingTool::Setup() creates an instance of an object called UMeshOpPreviewWithBackgroundCompute, which does most of the heavy lifting. This object (lets called it MOPWBC for short :P) implements a common UX pattern in which we want to edit a mesh based on a set of properties, and show a live preview, and we want the edit computation to run in a background thread so it doesn’t freeze the Editor. The “edit a mesh” operation is expressed as a FDynamicMeshOperator, and MeshProcessingTool.h defines a subclass FMeshProcessingOp that basically just owns and runs a lambda that edits the mesh. This lambda is provided by the ::MakeMeshProcessingFunction() we defined above. MOPWBC takes the FDynamicMeshOperator instance created by UMeshProcessingTool::MakeNewOperator(), gives it to a background thread to execute, and when the execution finishes, it uses the result mesh that was returned to update a UPreviewMesh instance that the MOPWBC also creates and manages (magic!).

UPreviewMesh is an independent utility object, that can be used to display the result of interactive mesh editing - it creates and manages a temporary Actor with a special mesh component (USimpleDynamicMeshComponent) that is faster to update than a normal UStaticMeshComponent. The input StaticMeshActor/Component are hidden while the Tool is active, and updated when you click the Accept button. If you click Cancel, they are never modified.

MeshProcessingPlugin Editor Mode, and Adding New Tools

The Mesh Processing Editor Mode is also provided by the Plugin. This is really getting into Unreal Editor dark arts, however what I have done here is basically a stripped down version of several built-in experimental Editor Modes - the ModelingToolsMode and SampleToolsMode Plugins (both located in /Engine/Plugins/Experimental/). The Modeling Tools Mode in particular has many more features than our basic mode (including icons!). In each case we have a subclass of FEdMode, which is how we get our own tab in the Editor Modes tab panel. You can create an FEdMode from scratch by selecting the Editor Mode type in the New Plugin dialog (like I said, dark arts).

The vast majority of the code at this level is boilerplate code you will won’t have any reason to modify. However if you want to add additional Tools - ie more buttons like “IGL Smooth” and “Export” in the toolbar - you will have to add 5 lines of code in specific places. Lets say your new tool is called UIGLSimplifyTool (perhaps based on libigl sample 703_Decimation) and you want the button to say “IGL Simplify”. Then you add the following lines:

1) In MeshProcessingPluginCommands.h, add a new command:

TSharedPtr<FUICommandInfo> BeginIGLSimplifyTool;

2) Configure that command in MeshProcessingPluginCommands.cpp:

UI_COMMAND(BeginIGLSimplifyTool, "IGLSimplify", "Start the LibIGL Simplify Tool", EUserInterfaceActionType::Button, FInputChord());

3) In MeshProcessingPluginEdMode.cpp, include your tool header and then in ::RegisterModeTools(), add a call to RegisterToolFunc() for your new Tool and Command:

#include "Tools/IGLSimlpifyTool.h"
...(snip)....
RegisterToolFunc(PluginCommands.BeginIGLSimplifyTool, TEXT("IGLSimplifyTool"), NewObject<UIGLSimplifyToolBuilder>());

4) in MeshProcessingPluginEdModeToolkit.cpp, in function ::BuildToolPalette(), add your new Command to the Toolbar.

ToolbarBuilder.AddToolBarButton(Commands.BeginIGLSimplifyTool);

That’s it! Done! New Tool appears in the Toolbar!

Modeling Mode in UE 4.24

I mentioned Modeling Mode several times above. This is another new Experimental feature of UE 4.24, which is built on the same Interactive Tools Framework that we used to create the IGLSmoothTool. It is much more extensive, and includes a variety of Mesh Editing and Repair Tools. By default this Mode Plugin is not enabled, and you have to open the Plugins browser and enable the Modeling Tools Editor Mode Plugin to turn it on. However in the IGLMeshProcessingProject I have already enabled it in the settings, so if you switch to the tab with the “Sphere-Cone-Box” icon, you will get a set of tabs and icons in the Mode Toolbar (Most Tools will be disabled unless you have a suitable object(s) selected):

View fullsize

Modeling Mode is relevant to this tutorial because there is a reasonable chance you might need to massage input data to experiment with mesh processing code. For example the FBX/OBJ importer frequently leaves “cracks” in objects along material boundaries. You can use the Inspector Tool to see if this is the case (it will highlight boundary edges in red), and if there are cracks, the Weld Edges Tool can probably repair them.

Another problem you might come across is that many game Assets have very coarse “low-poly” triangulations that are not suitable for most research geometry processing algorithms. The Remesh Tool can be used to add triangle density to these meshes without ruining the UV coordinates or hard normals. The image on the right shows the result of Remeshing the table from the standard UE scene.

The images below show the results of the IGLSmooth Tool on the default Table asset (left) and the remeshed triangulation (right). The remeshed version has better (ie more consistent and “smoother”) behavior because there is more freedom to move the vertices, and because numerically the “energy” that is minimized to compute the smoothed version is better-behaved numerically on more even triangulations. You can always use the Simplify Tool to get rid of these extra triangles after the processing. (PS: the Remesher in Unreal is incredibly powerful and you might find it quite useful to mix with libigl code! Check out RemeshMeshTool.cpp in the MeshModelingToolset plugin for sample code.)

View fullsize

Using Other Mesh Processing Code/Libraries

In this tutorial I focused on libigl because it is widely used, has a lot of neat sample code you can easily drop into an Unreal Editor Tool, and it’s header-only. Other header-only C++ libraries should be similarly-easy to use, the main “gotcha” is that Unreal configures the C++ compiler to consider all Warnings as Errors. As a result it may be necessary to disable some warnings to get your code to build. That’s what the file IGLIncludes.h does in the Mesh Processing Plugin, for example. (Of course you could also fix the warnings!)

If you want to use existing cpp files, things get a bit trickier. You have two options. One is to compile those separately into static libraries or DLLs and link to them. To do that you would add them in the MeshProcessingPlugin.Build.cs file. This is not trivial but there is a nice tutorial here (link) explaining how to do it for PCL, the Point Cloud Library. It’s from 2017 so the instructions should still apply (if you google you will likely find many older tutorials that are now out-of-date…).

The second option is to include your code (cpp and headers) directly within the /Private/ and/or /Public/ subdirectories of the Plugin Source folder. Then when you Regenerate Project Files (see step 3 above) your code will be automatically picked up by Unreal Build Tool (UBT) and included in the generated Visual Studio solution, and built into the Plugin’s DLL. This is in fact how many third-party libraries are included in Unreal Engine (there is actually a version of Eigen used in Unreal, it’s just quite out-of-date). Note however that there is not an easy way to exclude cpp files within the /Source/ subdirectory. This can trip up your attempts to just drop a full repository into the Plugin (for example Eigen’s repo includes a lot of cpp test and example code that UBT will try to build and link, unless those files are literally deleted.

Finally, UE4.24 by default configures the compiler to C++14. If your code requires C++17 or higher, it’s not hopeless. You can configure the Build.cs to enable this level of support for your plugin. The first post in this thread explains the lines to add. However that thread also describes some problems you might encounter. Good luck!

UE 4.26 Update

UE 4.26 introduced some changes to the Interactive Tools framework API, and the 4.24 tutorial code will no longer compile. I have ported it to 4.26 and made some updates. I kept the 4.24 version in the Github repo, and put the the 4.26 version in a separate path. If you would like to see the minimal changes necessary, see this commit. After that, I made further updates I will describe below. I also fixed an issue where the Eigen third-party code did not include any files or folders named ‘Core’, due to the .gitignore.

Another UE 4.26 addition is a “Base Tool” class named UBaseMeshProcessingTool. This was inspired by UMeshProcessingTool above, but with some useful additions. In the current 4.26 sample I have ported UMeshProcessingTool to use UBaseMeshProcessingTool. This intermediate might not be necessary anymore, but removing it meant adding quite a bit of boilerplate to the IGL tool, and rewriting some of the tutorial above, so I left it in. From the perspective of the IGL code, not much changed - the diff is here. The main difference is that I used the new PropertySet Watcher API to watch for changes in the properties, rather than a universal event handler.

One other important thing to know is that by default UBaseMeshProcessingTool will scale the input mesh to a unit box before calling any mesh processing code (and inverse-scale the corresponding live-preview and output meshes appropriately). This helps to “normalize” for the vast differences in scale that occur in a game environment, where we can easily have tiny rocks and enormous cliffs in the same scene. You can disable this behavior by overriding UBaseMeshProcessingTool::RequiresScaleNormalization(). Note that because of this normalization, I had to scale the 0-100 range of the Smoothness parameter presented in the UI (a standard complication in Laplacian mesh processing).

Finally two practical notes. First, make sure you install the Starter Content with the Engine, or you will have an empty level when you open the project. Second, UE has a file path limit when building. If you put the sample code in an already-long path, you might find that it won’t build, with errors about being unable to find files. If this is the case try moving the whole folder to a shorter path.

Surfacing Point Sets with Fast Winding Numbers

View fullsize

Winding number of different regions inside and outside a mesh with self-intersecting and overlapping components.

In my previous tutorial on creating a 3D bitmap from a triangle mesh, I used the Mesh Winding Number to robustly voxelize meshes, even if they had holes or overlapping self-intersecting components. The Mesh Winding Number tells us “how many times” a point p is “inside” a triangle mesh. It is zero when p is outside the mesh, 1 if it is inside one component, two if it is inside twice, and so on, as illustrated in the image on the right. The Winding Number is an integer if the mesh is fully closed, and if there are holes, it does something reasonable, so that we can still pick an isovalue (say 0.5) and get a closed surface.

This is a very powerful technique but it is also very slow. To compute the Mesh Winding Number (MWN) for a given point p, it is necessary to evaluate a relatively expensive trigonometric function for each triangle of the mesh. So that’s an O(N) evaluation for each voxel of an O(M^3) voxel grid. Slow.

The original Winding Number paper by Jacobson et al had a neat trick to optimize this evaluation, which takes advantage of the fact that if you are outside of the bounding box of an “open” patch of triangles, the summed winding number for those triangles is the same as the sum over a triangle fan that “closes off” the open boundary (because these two numbers need to sum to 0). We can use this to more efficiently evaluate the winding number for all the triangles inside a bounding box when p is outside that box, and this can be applied hierarchically in a bounding-box tree. This optimization is implemented in DMeshAABBTree3.WindingNumber(). However, although this gives a huge speedup, it is not huge enough - it can still take minutes to voxelize a mesh on a moderately-sized grid.

At SIGGRAPH 2018, I had the pleasure to co-author a paper titled Fast Winding Numbers for Soups and Clouds with Gavin Barill, Alec Jacobson, and David Levin, all from the University of Toronto’s DGP Lab, and Neil Dickson of SideFX. As you might have gathered from the title, this paper presents a fast approximation to the Mesh Winding Number, which also can be applied directly to surface point sets. If you are interested in C++ implementations, you can find them on the paper’s Project Page. In this tutorial I will describe (roughly) how the Fast Winding Number (FWN) works and how to use the C# implementation in my geometry3Sharp library, which you can find on Nuget or Github.

[Update 09-26-18] Twitter user @JSDBroughton pointed out that in the above discussion I claim that the Winding Number is an integer on closed meshes. This is true in the analytic-math sense, however when implemented in floating point, round-off error means we never get exactly 0 or 1. And, the approximation we will use below will introduce additional error. So, if you want an integer, use Math.Round(), or if you want an is-this-point-inside test, use Math.Abs(winding_number) > 0.5.

Fast Winding Number Approximation

The key idea behind the Fast Winding Number is that if you are “far away” from a set of triangles, the sum of their individual contributions to the overall mesh winding number can be well-approximated by a single function, ie instead of evaluating N things, you evaluate 1. In the Mesh Winding Number, the contribution of each triangle is it’s solid angle measured relative to evaluation point p. The figure on the right illustrates what the solid angle is - the area of the projection of the 3D triangle onto a sphere around p, which is called a spherical triangle.

When p is relatively close to the triangle, like in the figure, then any changes to the 3D triangle will have a big effect on this projected spherical triangle. However, if p is “far away” from the triangle, then its projection will be small and changes to the triangle vertices would hardly change the projected area at all. So, when the triangle is far away, we might be able to do a reasonable job of numerically approximating its contribution by replacing it with a small disc. In this case, instead of a 3D triangle we would have a point, a normal, and an area.

View fullsize

Of course, replacing an O(N) evaluation of triangles with an O(N) evaluation of discs would not be a big win. But, once we have this simplified form, then through some mathematical trickery, the spherical angle equation can be formulated as a mathematical object called a dipole. And the sum of a bunch of dipoles can be approximated by a single dipole, if you are far enough away. The figure on the right, taken from the paper, shows a 2D example, where the sum of 20 dipoles is approximated by a single stronger dipole. Even at relatively small distances from the cluster of dipoles, the scalar field of the sum is hardly affected by replacing the simplification.

This is how we get an order-of-magnitude speedup in the Winding Number evaluation. First we compute an axis-aligned bounding volume hierarchy for the mesh. Then at each internal node of the tree, we find the coefficients of a single dipole that approximate the winding number contributions for each triangle below that node. When we are evaluating the Winding Number later, if the evaluation point p is far enough away from this node’s bounding box, we can use the single-dipole approximation, otherwise we recursively descend into the node. Ultimately, only the triangles very near to p will actually have their analytic solid angles evaluated. The speedups are on the order of 10-100x, increasing as the mesh gets larger. It is…super awesome.

Also, since the dipole is a function at a point, we can apply this same machinery to a set of points that are not connected into triangles. We will still need a normal and an “area estimate” for each point (more on that below). But the result will the a 3D scalar field that has all the same properties as the Mesh Winding Number.

Mesh Fast Winding Number

There really isn’t much to say about using the Mesh Fast Winding Number. Instead of calling DMeshAABBTree3.WindingNumber(), call FastWindingNumber(). They behave exactly same way, except one is much faster, at the cost of a small amount of approximation error. Note that the internal data structures necessary to do the fast evaluation (ie the hierarchy of dipole approximation coefficents) are only computed on the first call (for both functions). So if you are planning to do multi-threaded evaluation for many points, you need to call it once before you start:

DMeshAABBTree3 bvtree = new DMeshAABBTree3(mesh, true);
bvtree.FastWindingNumber(Vector3d.Zero);   // build approximation
gParallel.ForEach(list_of_points, (p) => {
    double winding_num = bvtree.FastWindingNumber(p);
});

There are a few small knobs you can tweak. Although the paper provides formulas for up to a 3rd order approximation, the current g3Sharp implementation is only second-order (we don’t have a third-order tensor yet). You can configure the order you want using the DMeshAABBTree3.FWNApproxOrder parameter. First order is faster but less accurate. Similarly, the parameter DMeshAABBTree3.FWNBeta controls what “far away” means in the evaluation. This is set at 2.0, as in the paper. If you make this smaller, the evaluation will be faster but the numerical error will be higher (I have never had any need to change this value).

Point Fast Winding Number

geometry3Sharp also has an implementation of the Fast Winding Number for point sets. This involves several interfaces and classes I haven’t covered in a previous tutorial. The main class we will need to use is PointAABBTree3, which works just like the Mesh variant. However, instead of a DMesh3, it takes an implementation of the IPointSet interface. This interface just provides a list of indexed vertices, as well as optional normals and colors. In fact DMesh3 implements IPointSet, and works fine with “only” vertices. So we can use a DMesh3 to store a point set and build a PointAABTree3, or you can provide your own IPointSet implementation.

To test the Point Fast Winding Number implementation, we will use a mesh of a sphere. Here is a bit of sample code that sets things up:

Sphere3Generator_NormalizedCube gen = new Sphere3Generator_NormalizedCube() { EdgeVertices = 20 };
DMesh3 mesh = gen.Generate().MakeDMesh();
MeshNormals.QuickCompute(mesh);
PointAABBTree3 pointBVTree = new PointAABBTree3(mesh, true);

Now, I mentioned above that each point needs a normal and an area. We computed the normals above. But the per-point areas have a big effect on the resulting iso-surface, and there is no standard “right way” to compute this. In this case, since we know the point sampling of the sphere is approximately regular, we will assume the “area” of each point should be a disc around it, with radius equal to half the average point-spacing. Here is a way to calculate this:

double mine, maxe, avge;
MeshQueries.EdgeLengthStats(mesh, out mine, out maxe, out avge);
Circle2d circ = new Circle2d(Vector2d.Zero, avge * 0.5);
double vtxArea = circ.Area;

The way we tell PointAABBTree3 about the per-vertex area estimates is to provide an implementation of the lambda function FWNAreaEstimateF:

pointBVTree.FWNAreaEstimateF = (vid) => {
    return vtxArea;
};

Now we can call pointBVTree.FastWindingNumber(), just like the mesh version. Now, say you would like to generate a mesh surface for this winding number field. We can easily do this using the MarchingCubes class. We just need to provide an ImplicitFunction3d implementation. The following will suffice:

class PWNImplicit : BoundedImplicitFunction3d {
    public PointAABBTree3 Spatial;
    public AxisAlignedBox3d Bounds() { return Spatial.Bounds; }
    public double Value(ref Vector3d pt) {
        return -(Spatial.FastWindingNumber(pt) - 0.5);
    }
}

Basically all we are doing here is shifting the value so that when the winding number is 0, ie “outside”, the scalar field value is -0.5, while it is 0.5 on the “inside”, and 0 at our “winding isosurface”, where the winding number is 0.5. We have to then negate these values because all our implicit surface machinery assumes that negative == inside.

Finally, this bit of code will do the surfacing, like in our previous implicit surface tutorials. Note that here we are using a cube resolution of 128, you can reduce this for quicker, lower-resolution results. It is also quite important to use the Bisection root-finding mode. The default is to use linear interpolation, but because of the “shape” of the winding number field, this will not work (as is described in the paper).

MarchingCubes mc = new MarchingCubes();
mc.Implicit = new PWNImplicit() { Spatial = pointSpatial };
mc.IsoValue = 0.0;
mc.CubeSize = pointSpatial.Bounds.MaxDim / 128;
mc.Bounds = pointSpatial.Bounds.Expanded(mc.CubeSize * 3);
mc.RootMode = MarchingCubes.RootfindingModes.Bisection;
mc.Generate();
DMesh3 resultMesh = mc.Mesh;

The result of running this code is, as expected, a mesh of a sphere. Not particularly exciting. But the point is, the input data was in fact just a set of points, normals, and areas, and through the magic of the Point Fast Winding Number, we turned that data into a 3D isosurface.

Area Estimates and Scan Surface Reconstruction

In the example above, we were cheating because we knew the point cloud came from a sphere, and specifically from a quite regular mesh of the sphere. This made it easy to get a sensible per-vertex area estimate. What if our estimate was not so good? An interesting experiment is just to scale our fixed per-vertex area. In the example below, we have the “correct” result on the left, and then the result with the area scaled by 2x, 4x, and 0.5x. The effects are neat, but also…not ideal for surface reconstruction.

View fullsize

Unfortunately there is no “right” way to assign an area to each point in a point cloud (in fact there is no “right” way to assign normals, either!). The Fast Winding Number paper describes a method based on using Delaunay Triangulations in local 2D planar projections around each point. This is a great way to do it, but it also involves several complicated steps, and can take quite a bit of time for a large point set. So, we’ll try something simpler below.

View fullsize

But first, we need a point set. For this test I will use a “real” point set, rather than a nice “synthetic” one that is sampled from a known triangle mesh. I am going to use the Chinese Dragon sample scan from the AIM@SHAPE 3D model repository. Actually I just used the “upper” scan, which contains 1,766,811 points, in XYZ format, which is a simple list of point positions and normals. You can directly open and view XYZ point cloud files Meshlab, a few screenshots are shown to the right. As you can see, the scan points are spaced very irregularly, and there are huge regions with no data at all! So, we cannot expect a perfect reconstruction. But if we could get a watertight mesh, then we can take that mesh downstream to tools where we could, for example, 3D sculpt the mesh to fix the regions where data was missing, take measurements for digital heritage applications, or just 3D print it.

Since the scanner provided (approximate) surface normals, the main thing we need to do is estimate an area for each point. This area clearly needs to vary per-point. We’ll try something just slightly more complicated than we did on the sphere - we’ll find the nearest-neighbour to each point, and use the distance to that point as the radius of a disc. The disc area will then be the point radius. Here’s the code:

DMesh3 pointSet = (load XYZ file here...)

// estimate point area based on nearest-neighbour distance
double[] areas = new double[pointSet.MaxVertexID];
foreach (int vid in pointSet.VertexIndices()) {
    bvtree.PointFilterF = (i) => { return i != vid; };   // otherwise vid is nearest to vid!
    int near_vid = bvtree.FindNearestPoint(pointSet.GetVertex(vid));
    double dist = pointSet.GetVertex(vid).Distance(pointSet.GetVertex(near_vid));
    areas[vid] = Circle2d.RadiusArea(dist);
}    
bvtree.FWNAreaEstimateF = (vid) => {
    return areas[vid];
};

Note that this is not the most efficient way to compute nearest-neighbours. It’s just convenient. Now we can run the MarchingCubes surfacing of the Point-Set Winding Number Field defined with these areas. The result is surprisingly good (I was, in fact, literally surprised by how well this worked - the first time, no less!). The images below-far-left and below-far-right show the raw Marching Cubes output mesh, at “256” resolution. There is some surface noise, but a Remeshing pass, as described in a previous tutorial, does a reasonable job of cleaning that up (middle-left and middle-right images). The only immediately-obvious artifact of the dirty hack we used to estimate surface areas seems to be that in a few very sparsely sampled areas (like the rear left toe) the surface was lost.

View fullsize

View fullsize

In areas where there were no surface points, the winding field has produced a reasonable fill surface. I can’t quite say “smooth” because one artifact of the Fast Winding Number approximation is that in the “far field”, ringing artifacts can be visible. This is an artifact of using a hierarchical evaluation of a functional approximation. At each point in space we have to make a decision about whether to use a finer approximation or not, and this decision varies over space. (One potential fix here would be to smoothly transition or“blend” between approximations at different levels, instead of picking one or the other - something for a reader to implement?)

Summary

Traditionally, determining point containment for an arbitrary 3D mesh has been problematic to use in many applications because there wasn’t a great way to compute it. Raycast parity-counting is not efficient and can go horribly wrong if the mesh has imperfections, and voxelizing is memory-intensive and similarly fails on many real-world meshes. The Mesh Winding Number provides a much better solution, and the Fast Winding Number approximation makes it practical to use, even on huge meshes at runtime.

For example I have encountered many situations in building VR user interfaces where I want to be able to check if a point (eg on a spatial controller) is inside a 3D UI element (eg for selection). In most cases I would need to approximate the UI element with simpler geometric bounding-objects that support analytic containment tests. With the Fast Winding Number, we can now do these tests directly on the UI element.

Remeshing and Mesh Constraints

Recently geometry3Sharp user samyuchao asked a question about a topic I've been meaning to write about for nearly a year. The question was, for the mesh on the right, how to re-triangulate it so that the triangles are uniform but the boundary shape is preserved. This can easily be done with the geometry3Sharp Remesher class, with just a few lines of code. 

Before we begin, I'll just mention that although this tutorial is about using the Remesher directly from C#, you can do the same experiments using the Remesh Tool in Gradientspace's Cotangent app, because it uses the same Remesher class internally. You can get Cotangent here. 

The Remesher class works much like the Reducer class I covered in a previous tutorial. In fact they both inherit from MeshRefinerBase which provides common functionality based on the MeshConstraints we will use below. Here is the minimal code to run a remesh:

DMesh3 mesh = load_my_mesh_somehow();
Remesher r = new Remesher(mesh);
r.PreventNormalFlips = true;
r.SetTargetEdgeLength(0.5);
for ( int k = 0; k < 20; ++k )
    r.BasicRemeshPass();

View fullsize

If we run this code on our standard bunny mesh, we get the result to the right. There are a few things to explain here. First of all, the goal of Remesher is to create a uniform or isotropic mesh. So, we give it an edge-length goal, and it tries to convert the input mesh into one where all the edges have that length. In fact, as I will explain below we need to give it both a minimum and maximum edge length, because we can't achieve exactly a specific length. The function SetTargetEdgeLength() sets suitable min/max lengths based on the given goal length, but you can also directly set .MinEdgeLength and .MaxEdgeLength. Note that this is an absolute length, so it needs to be defined to a value that makes sense for your input mesh (in this case our standard bunny has an average edge length of 1.0, which keeps things simple). See below for tips about calculating a relative edge length.

Next we do 20 iterations of BasicRemeshPass(). I will explain what this does below, but the main thing to understand is that Remesher does iterative mesh refinement or mesh optimization. That means we take "steps" towards our goal, in the form of passes. More passes means better results, but also more compute time. 

View fullsize

You may also have noticed that in the above-right example, the surface has been smoothed out. This is because our mesh refinement is combined with mesh smoothing. This smoothing is necessary to achieve the reguarly-shaped triangles, but as an artifact the surface shrinks. The .SmoothSpeedT property controls how quickly the smoothing happens. More passes means more smoothing, which can mean that if you want to get a very regular triangulation, your object will shrink a lot. Maybe this is what you want, though! In the grid of images to the right, SmoothSpeedT is set to 0.1, 0.25, and 1.0 in the 3 rows, and the columns are after 20, 40, and 60 iterations. In this case I used a target edge length of 1 (Click on this image to make it bigger).

Projection Targets

Most of the time where we would like to use remeshing, we don't want to smooth out the shape so drastically. We just want to improve the mesh quality and/or modify triangle density. To preserve the shape we need to reproject the evolving mesh onto the input surface. We can do this with a slight modification to the Remesher setup:

r.SetTargetEdgeLength(0.75);
r.SmoothSpeedT = 0.5;
r.SetProjectionTarget(MeshProjectionTarget.Auto(mesh));
(...remesh passes...)

MeshProjectionTarget.Auto() is a utility function that copies the input mesh and creates a DMeshAABBTree3 bounding-box hierarchy (which I covered in a previous tutorial). A copy is required here because we are going to modify the mesh in Remesher, if you already have a copy lying around, MeshProjectionTarget has other constructors that can re-use it. Here's the result of running this code for 20 iterations with SmoothSpeedT = 0.1 and 0.5:

View fullsize

In this case we can see that SmoothSpeedT has a different effect - the triangulation is much less regular in the middle image. This is what happens when you increase triangle density but smooth slowly - the triangles do not have "time" to redistribute themselves evenly. You might be thinking, well why don't I just always crank it up to 11 (or 1 in this case)? Well, here is another example:

View fullsize

In the leftmost image we set the target length to 1.5 (so, larger triangles than our initial mesh) and SmoothSpeedT to 1. The thin areas of the ears have eroded away. What happens in this case is that as we smooth and reproject the vertices, they tend to clip off bits of the thin extremities each pass. Because we are taking large smoothing steps, this happens very quickly. If we take smaller steps (SmoothSpeedT=0.1 in the middle), this happens more slowly. On the right, we have set a configuration flag Remesher.ProjectionMode = Remesher.TargetProjectionMode.Inline. Normally, we compute a smoothing pass, and then a projection pass. When we set the projection mode to Inline, we immediately compute the projected position of each vertex. This is less efficient but can reduce erosion of the thin features.

View fullsize

However, ultimately, Remesher is not a great way to drastically reduce the resolution of a mesh, because of the smoothing process (unless you have constraints that will preserve features, more on this below). Reducer is a much better choice if you want to really minimize triangle counts.

Note also that you can actually use any surface as the projection target, or even use more complicated programmatic projection targets. You can get many interesting effects this way. For example, in the screenshot on the right I am using Cotangent's Map To Target Tool in Bounded mode, to remesh the green bunny using the purple box as the target. This mode uses a custom projection target that smoothly blends between projecting onto the box, and projecting onto the bunny, based on a distance falloff. This produces a kind of surface-blending operation that would be quite difficult to achieve any other way. 

How does it work?

As I mentioned above, the Remesher class uses an implementation of iterative mesh refinement. What "iterative" means here is that we make passes over the mesh and in each pass we make improvements that get us closer to our goal (in this case a uniform mesh). Further down the page there are a few videos that show the evolving state of a mesh after each pass.

Inside each pass, we iterate over the edges of the mesh and apply one three operations - Flip, Split, or Collapse. The diagram to the right shows what happens in each of these operations. A Flip (sometimes called an edge "rotation") replaces two triangles with two new  triangles. A Split replaces two triangles with four new ones, by adding a vertex. By default this vertex is placed on the original edge, so a Split is the one operator we can do that is guaranteed to not change the mesh shape. Finally Collapse is used to remove an edge. This is is the most drastic change (and hardest to implement correctly!) because the one-rings of all four vertices of the initial triangle-pair are affected.

Mesh boundary edges can be can Split and Collapsed, but not Flipped. The DMesh3 implementations of these operations - SplitEdge(), CollapseEdge(), and FlipEdge(), will also not allow changes that would result in non-manifold mesh topology, such as an edge with more than two connected triangles. 

As I mentioned above, These edge operators are combined with mesh smoothing. The Remesher uses standard Laplacian smoothing with uniform weights, which maximizes inner fairness, ie triangle regularity. Unfortunately it also means the shape changes the most quickly. If you have a case where the triangle shapes need to be preserved (for example if the mesh has UVs), you can try changing the .SmoothType property - Cotangent and Mean Value weights are also implemented. 

Since the edge operators and smoothing are all applied locally, the order of operations matters - we call this the "remeshing policy". A standard approach is to do passes of each operator. Remesher does not do this as it results in much wasted work on large meshes, particularly as the mesh converges (just checking if we need to flip any edges on a million triangles is quite expensive). The policy in Remesher is as follows:

foreach ( edge in current_mesh ) {
    if ( edge too short ) collapse_edge();
    elif ( edge needs flip ) flip_edge();
    elif ( edge too long ) split_edge();
}
smooth_all_vertices();
reproject_all_vertices();

The outer steps are defined in BasicRemeshPass() and ProcessEdge(). The code for each of the inner steps is relatively clearly demarcated, and should be relatively easy to cut-and-paste if you wanted to re-organize this into separate flip/split/collapse passes. If you are interested in the academic research behind this, Remesher is in large part an implementation of the techniques described in A Remeshing Approach to Multiresolution Modeling (Botsch and Kobbelt, SGP 2004).

Boundary Constraints

View fullsize

So far we've been dealing with close meshes, but the original question was about a mesh with an open boundary. What happens if we run the code above on a mesh-with-boundary? Nothing good! As the boundary vertices are smoothed, some of the edges get shorter and are collapsed, which basically means that the open boundary erodes away. 

To fix this we will need to configure Remesher.Constraints, which is an instance of the MeshConstraints class. This class allows you to set constraints on the mesh edges and vertices, based on their IDs. Edges can be restricted so that they can't be flipped, collapsed, split, or any combination of these. Edges can also be associated with a particular IProjectionTarget. Similarly vertices can be constrained to be fixed in place, or allowed to slide along an IProjectionTarget.

To constrain the open boundaries of a mesh, we can use the helper class MeshConstraintsUtil as follows:

Remesher r = new Remesher(mesh)
MeshConstraintUtil.FixAllBoundaryEdges(r);

This will create a MeshConstraints instance and populate it with the boundary edge and vertex constraints. It's actually only a few lines of code, so if you want to experiment with setting up your own constraints, this is a good starting point. For these examples I'll use a flat mesh with boundary as it's easier to see what is happening. On the left we have the input mesh, and in the middle is the result using the above constraints. As you can see, the boundary is preserved. In fact it has been exactly preserved - exact same vertices in the same locations. This can be useful (eg if you want to remesh in parts and stitch back together later) but it does mean that there will be ugly triangles around the border, just like in samyuchao's example. So how do we get to the example on the right?

View fullsize

Instead of FixAllBoundaryEdges(), we can use the following:

MeshConstraintUtil.PreserveBoundaryLoops(r);

Although it's also just one call, internally this works in a completely different way. First it creates a MeshBoundaryLoops instance, which walks over the mesh and finds chains of open boundary edges (in this case there is just one) as EdgeLoop objects. These are converted to DCurve3 curves, which are basically 3D poly-lines. Then a DCurve3ProjectionTarget is created, which projects input points onto the curve. Finally the vertices and edges of the EdgeLoop are constrained such that the edges can be modified, but the vertices slide along this boundary loop. The result is a retriangulation where the boundary shape is preserved.

Except for one last thing. When using this approach, thin triangles will often be created on the boundary as a result of flipping boundary-adjacent edges. Currently I do not automatically remove these slivers (I might change this in the future). To remove these 'fin' triangles you can call MeshEditor.RemoveFinTriangles(mesh) after you are done with the remesh passes. That's what I did to create the rightmost example above.

Ok, one last constraint example. Lets say you had a mesh with triangles grouped into sets - Face Groups, to follow the terminology used in Meshmixer, which has a nice toolset for doing this kind of segmentation. An example cylinder with separate groups is shown below-left, which I exported from Meshmixer (the geometry3Sharp OBJ loader can read and writer Meshmixer-style face groups). A standard remesh pass will not preserve the crisp edges of this input mesh, as in the result below-middle. However, this snippet:

int set_id = 1;
int[][] group_tri_sets = FaceGroupUtil.FindTriangleSetsByGroup(mesh);
foreach (int[] tri_list in group_tri_sets) {
    MeshRegionBoundaryLoops loops = new MeshRegionBoundaryLoops(mesh, tri_list);
    foreach (EdgeLoop loop in loops) {
        MeshConstraintUtil.ConstrainVtxLoopTo(r, loop.Vertices, 
            new DCurveProjectionTarget(loop.ToCurve()), set_id++);
    }
 }

View fullsize

Will produce the rightmost example, where the group-region-border-loops have been preserved. This works similar to the PreserveBoundaryLoops() call above. First we find the triangle set for each face group using FaceGroupUtil.FindTriangleSetsByGroup(). Then for each set we construct a MeshRegionBoundaryLoops object, which will find the boundary paths of the selection as a set of EdgeLoop objects. Note that if the boundary topology had T-junctions, this would also return EdgeSpans and you would need to handle that case. Finally for each loop we call ConstrainVtxLoopTo to constrain the edgeloop vertices/edges to the DCurve3 polyline formed by that edge loop. Whew! 

Unity Remeshing Animation

One of my favorite things about C# is that, combined with the Unity 3D development environment, it is very easy to animate the guts of geometry algorithms. C# makes it easy to expose internal steps of an algorithm as something you can enumerate over at a higher level, and Unity makes it easy to run one of those enumerations with an arbitrary time delay between updates. I'll make this a topic of a future tutorial, but basically, this is all the code that I needed to create the animations below:

IEnumerator remeshing_animation() {
    foreach (int i in interactive_remesh(remesh, RemeshPasses)) {
        g3UnityUtils.SetGOMesh(meshGO, curMesh);
        yield return new WaitForSecondsRealtime(1.0f);
    }
}
IEnumerable<int> interactive_remesh(Remesher r, int nPasses) {
    for (int k = 0; k < nPasses; ++k) {
        r.BasicRemeshPass();
        yield return k;
    }
}

Then I can just initialize the remesh object and call StartCoroutine(remesh_playback()) to kick off the animation. The function g3UnityUtils.SetGOMesh() is a utility function that is included in the geometry3UnityDemos repo on the Gradientspace github, along with the scene I used to create the animations below (called remesh_demo). On the right you can see that although most of the mesh converges quickly, the ears continue to oscillate. This is the kind of thing that is quite difficult to tell from profiling, but jumps right out at you when you see the algorithm in-progress. If I want to inspect in more detail I can just hit pause in the Unity editor, easily add debug geometry, expose parameters that I can tweak at runtime in the Editor UI, and so many other things. But that's for a future tutorial!

Tips and Tricks

One thing you might find yourself wanting to do is to remesh with a "relative" density. For example if you have an input mesh you might want one with "half the edge length", approximately. One way to accomplish this is:

double min_edge_len, max_edge_len, avg_edge_len;
MeshQueries.EdgeLengthStats(mesh, out min_edge_len, out max_edge_len, out avg_edge_len);
r.SetTargetEdgeLength(avg_edge_len * 0.5);

So basically we are using the average mesh edge length as the "current" edge length and scaling it. There are variants of EdgeLengthStats() that can measure specific edge sets, which might be useful if for example you want to remesh relative to a boundary-loop vertex density.

There is another small extension of Remesher to specifically handle the case where you have an open boundary loop that you want to resample or clean up for further processing. This can be handled via the constraint functions above, but then you will have to "find" the boundary loop again, because your input loop edge/vertex indices will no longer be valid. Instead use the EdgeLoopRemesher class, which can limit changes to the loop itself or a border band, and will track changes so you can find the output boundary loop.

Ok that's it for this tutorial. I hope it is helpful. And if you are using Remesher in a production application where performance matters, I'd just like to mention that I have non-open-source extensions to this base class that can often significantly improve performance (these are used in Cotangent if you want to compare). If you are interested in licensing this more advanced Remesher, please get in touch.

Direct 3D Printer Control - Part 1

This is the first of a series of posts about how to directly generate GCode for your 3D printer. In the last article I demonstrated how to turn a mesh into GCode with about 12 lines of code. That's fine if you want to experiment with meshes. But what if you want to control the printer yourself? The Gradientspace Slicer is designed to make this easy at several different levels. 

To start, you'll need the geometry3Sharp, gsGCode, and gsSlicer libraries. If you check out the gsSlicerApps repository, this is all set up for you, and you'll find the sample code below in the GeneratedPathsDemo Visual Studio project.

Ok, here is the basic harness we will use for all our examples. This is largely boilerplate code, however you will need to use the right Settings object for your printer (assuming it's explicitly supported, otherwise you can try RepRapSettings, it will work with many printers). And you might need to modify some fields in the Settings. But otherwise you don't need to change this code, we'll just fill in the middle bit

// You'll need the Settings object suitable for your printer
RepRapSettings settings = new RepRapSettings();
// you can customize the settings below
settings.ExtruderTempC = 200;

// we want to accumulate the gcode commands to a GCodeFile
var gcode_accumulator = new GCodeFileAccumulator();
var builder = new GCodeBuilder(gcode_accumulator);

// the Compiler turns 2D/3D paths into GCode commands
SingleMaterialFFFCompiler compiler = new SingleMaterialFFFCompiler(
    builder, settings, RepRapAssembler.Factory);

compiler.Begin();

// (THIS IS WHERE WE ADD TOOLPATHS)

compiler.End();

// this bit writes out the GCodeFile to a .gcode file
GCodeFile gcode = gcode_accumulator.File;
using (StreamWriter w = new StreamWriter("c:\\demo\\generated.gcode")) {
    StandardGCodeWriter writer = new StandardGCodeWriter();
    writer.WriteFile(gcode, w);
}

Before we continue, a bit about the gsSlicer/gsGCode architecture and terminology. The basic idea here is that most of the time we want to be working at a higher level then GCode commands. We want to be able to define the geometric paths the print head will move along at the level of 2D/3D polygons and polylines. These are called Toolpaths.  We will build up ToolpathSet objects, which are just lists of IToolpath instances, and then pass these to a Compiler that will sort out how to turn them into GCode. 

The Compiler level is intended to support other outputs besides gcode, like laser paths for an SLS machine. The SingleMaterialFFFCompiler is suitable for use with 3-axis single-material FDM/FFF 3D printers. Internally, this Compiler creates an IDepositionAssembler instance, which currently is always a subclass of BaseDepositionAssembler. The Assembler provides lower-level commands like MoveTo, ExtrudeTo, and so on, which map more directly to actual GCode commands. The GCodeBuilder we created above is used by the Assembler to emit GCodeLine objects into a GCodeFile.

If that was confusing, here's a diagram. The basic idea is that, you can pass Toolpaths to the Compiler, and it will look at them and decide how to best turn them into lower-level commands that the Assembler will be able to translate into machine-specific GCode. This is what SingleMaterialFFFPrintGenerator does internally. That class takes the mesh slices and figures out how to fill them with Toolpaths, which it then compiles. But we can also generate Toolpaths directly with code, and send them to the Compiler. Or, we could skip over the Compiler entirely, and use the Assembler. You can even use the GCodeBuilder interface, if you really want to control every aspect of the printer (or program some other kind of machine). 

The Compiler/Assembler terminology here is borrowed from programming language compilers. I think about it the same way. GCode is very analogous to CPU assembly language - both are lists of very simple structured text commands, (mostly) evaluated in-order. If we push this analogy, we could think of Toolpaths as the "C" of 3D printers, and Meshes are perhaps a high-level scripting language. 

In this post we'll focus on the Toolpath level. To simplify the creation of Toolpaths we'll use a helper class called ToolpathSetBuilder. This class knows how to transform basic geometry3Sharp classes like Polygon2d into ToolpathSet objects, which are a bit more complicated. Here is a function that compiles a vertical stack of circles, to make a tube. You would call this function in the "// THIS IS WHERE WE ADD TOOLPATHS" space above.

static void generate_stacked_polygon(SingleMaterialFFFCompiler compiler,
    SingleMaterialFFFSettings settings)
{
    int NLayers = 10;
    for (int layer_i = 0; layer_i < NLayers; ++layer_i) {        
        // create data structures for organizing this layer
        ToolpathSetBuilder layer_builder = new ToolpathSetBuilder();
        SequentialScheduler2d scheduler = new SequentialScheduler2d(layer_builder, settings);
        if (layer_i == 0)  // go slower on first layer
            scheduler.SpeedHint = SchedulerSpeedHint.Careful;

        // initialize and layer-up
        layer_builder.Initialize(compiler.NozzlePosition);
        layer_builder.AppendZChange(settings.LayerHeightMM, settings.ZTravelSpeed);

        // schedule a circle
        FillPolygon2d circle_poly = new FillPolygon2d(Polygon2d.MakeCircle(25.0f, 64));
        circle_poly.TypeFlags = FillTypeFlags.OuterPerimeter;
        scheduler.AppendPolygon2d(circle_poly);

        // pass paths to compiler
        compiler.AppendPaths(layer_builder.Paths, settings);
    }
}

As you can see, there really is not much to it. We create and initialize a ToolpathSetBuilder, add a Toolpath that moves up one layer in Z, and then add a second Toolpath that extrudes a circular polygon. We pass these to the Compiler, and repeat 10 times. The only extra bit is the SequentialScheduler2d. In many cases we would like to be able to add a set of Toolpaths and have the library figure out the best order to print them. This is what the Scheduler is for. Here we are using the dumbest possible Scheduler, that just passes on the paths in-order. SortingScheduler2d is an alternative that tries to be a bit smarter (but wouldn't matter here).

Ok, run this, get the .gcode file, and print it. You should get the result above right.

We made a tube - exciting! Now you know how to extrude any 2D outline that you can generate in code, without having to make a mesh. Here's another example, where I apply a simple deformation to the circle that varies with height. First we need a few parameters:

double height = 20.0;  // mm
int NLayers = (int)(height / settings.LayerHeightMM);  // 20mm
int NSteps = 128;
double radius = 15.0;
double frequency = 6;
double scale = 5.0;

Now replace the line that generates circle_poly above with this block:

// start with circle
FillPolygon2d circle_poly = new FillPolygon2d(Polygon2d.MakeCircle(radius, NSteps));

// apply a wave deformation to circle, with wave height increasing with Z
double layer_scale = MathUtil.Lerp(0, scale, (double)layer_i / (double)NLayers);
for ( int i = 0; i < NSteps; ++i ) {
    Vector2d v = circle_poly[i];
    double angle = Math.Atan2(v.y, v.x);
    double r = v.Length;
    r += layer_scale * Math.Sin(frequency * angle);
    circle_poly[i] = r * v.Normalized;
}

Run it, print it, and you should get the shape on the right. 

That's it for this tutorial. Next time we'll go further down the stack and generate individual print-head moves. But first, just a bit about how this ties into mesh toolpathing. What we've done above is exactly what SingleMaterialFFFPrintGenerator is doing. However instead of directly using the mesh slice polygons as toolpaths, the PrintGenerator uses various toolpathing strategies to fill in each polygon with nested perimeters, dense and sparse infill, support, and so on. These are all done by IFillPolygon implementations like ShellsFillPolygon. Each of these classes takes an input polygon and outputs a set of 2D polygon and polyline Toolpaths that are passed to the layer Scheduler, exactly like we did above.

You can also use these toolpathing classes yourself. So, if you wanted to do standard shells-and-infill for your procedurally-generated polygons, you could use a ShellsFillPolygon to create the perimeter toolpaths. This class also returns the "inner" polygons, which you could then pass to a SparseLinesFillPolygon to get the infill toolpaths. Easy! 

Mesh to GCode with gsSlicer

Most of the tutorials I've written so far have focused on geometry3Sharp, my geometry-processing library. But that's not my only commercial-friendly open-source library. I've also been working on another one, for 3D printing. In this tutorial, we'll use this library to convert a mesh to a GCode file that can be 3D printed. 

The gsSlicer library is in the gradientspace github, and we'll also need the gsGCode library. Combined, these three components - geometry3Sharp, gsSlicer, and gsGCode - have everything we need to build a command-line slicing tool. The gsSlicer library takes meshes as input, converts the meshes to a stack of planar slice polygons, and fills in those "2D solids" with paths ("toolpaths"). These are passed on down to gsGCode, which generates and manipulates GCode. If you aren't familiar, GCode is the command language used by most FDM/FFF 3D printers, and also by many other types of CNC machine. A GCode file is just a long list of of very simple commands - "move to x,y" and so on. In addition to generating GCode output, gsGCode can parse GCode files into various representations, including back into 2D/3D path geometry.

If you would like to avoid figuring out how to get all these libraries connected together, you can just check out the gsSlicerApps repository. This repo includes the others as submodules, and has various demo programs, including a 2D slice viewer which we will use below. Since everything is pure C#, you can open the solution file on windows or OSX using Visual Studio For Mac. The code I will explain below is taken directly from the MeshToGCodeDemo project in this solution.

A small caveat: gsSlicer is under active development, it's not (yet!) at the point where you should be throwing out your other printing tools. In terms of standard slicer capabilities, the one thing missing right now is bridging. Support structures are available but still a work-in-progress. And there are also lots of small tweaks that have yet to be done. But, if you want to experiment with printing from code, or try your own toolpathing techniques, I think you'll find gsSlicer is much cleaner and more straightforward than the other available open-source slicers, and you have the very strong toolset in geometry3Sharp to build on.

Ok, step 1 - we need a mesh. You could load one using StandardMeshReader, but I'll generate a cone procedurally instead:

CappedCylinderGenerator cylgen = new CappedCylinderGenerator() {
    BaseRadius = 10, TopRadius = 5, Height = 20, Slices = 32
};
DMesh3 mesh = cylgen.Generate().MakeDMesh();
MeshTransforms.ConvertYUpToZUp(mesh);       // g3 meshes are usually Y-up

// center mesh above origin
AxisAlignedBox3d bounds = mesh.CachedBounds;
Vector3d baseCenterPt = bounds.Center - bounds.Extents.z*Vector3d.AxisZ;
MeshTransforms.Translate(mesh, -baseCenterPt);

The only thing of note here is the call to ConvertYUpToZUp(). A problem you are likely to have already encountered in 3D printing is that many mesh modeling tools assume that "up" is the Y axis, but 3D printing tools always use the Z axis as up. If you load an STL file, this might not be necessary (but neither the STL or OBJ formats stores the up direction in the file).

View fullsize

Ok, next we create a PrintMeshAssembly, which in this case is just one mesh. However, gsSlicer has some advantages here over most existing slicers. For example, overlapping mesh components will be handled correctly in the vast majority of cases. You can also add open meshes to the assembly, and they will be printed as single-line-wide paths, like in the image on the right. And you can tag meshes as "support", in which case they are subtracted from the solids. 

// create print mesh set
PrintMeshAssembly meshes = new PrintMeshAssembly();
meshes.AddMesh(mesh, PrintMeshOptions.Default);

Next we need a Settings object. Currently gsSlicer does not support a very wide range of printers. However, the majority of printers out there use RepRap-style GCode, and so RepRapSettings will work fine with those machines. You will need to modify a few fields in the Settings though. In Settings.Machine, you will find the print bed dimensions, the nozzle and filament diameter, and the heated bed control. The Settings object has fields for the extruder and bed temperature, retraction, and the various print speeds. If you test a printer and it works, or it doesn't but you're willing to do some experimentation, let me know!

// create settings
MakerbotSettings settings = new MakerbotSettings(Makerbot.Models.Replicator2);
//PrintrbotSettings settings = new PrintrbotSettings(Printrbot.Models.Plus);
//RepRapSettings settings = new RepRapSettings(RepRap.Models.Unknown);

Ok, in the next few lines we will use MeshPlanarSlicer to convert the PrintMeshAssembly into a PlanarSliceStack, which is a list of per-layer 2D polygons and polyline paths. There's not really any options here, although if you are experimenting with open meshes you might need to tweak MeshPlanarSlicer.OpenPathDefaultWidthMM. 

// do slicing
MeshPlanarSlicer slicer = new MeshPlanarSlicer() {
    LayerHeightMM = settings.LayerHeightMM };
slicer.Add(meshes);
PlanarSliceStack slices = slicer.Compute();

And we're almost done, just one last block to do the toolpathing and write out the GCode. I will point out here that although the SingleMaterialFFFPrintGenerator does take the mesh assembly as input, the printing is entirely driven off the slices. So, you don't have to use MeshPlanarSlicer. In fact, you don't have to use a mesh at all! You can construct a 2D polygon stack in many other ways, and print it using this next block.

// run print generator
SingleMaterialFFFPrintGenerator printGen =
    new SingleMaterialFFFPrintGenerator(meshes, slices, settings);
if ( printGen.Generate() ) {
    // export gcode
    GCodeFile gcode = printGen.Result;
    using (StreamWriter w = new StreamWriter("c:\\demo\\cone.gcode")) {
        StandardGCodeWriter writer = new StandardGCodeWriter();
        writer.WriteFile(gcode, w);
    }
}

Basically, printGen.Generate() does all the work here, and if you try a large model, this will take some time - possibly several minutes (having more cores helps!). But, load the GCode onto your printer and within a few minutes (7, on my ancient-but-so-reliable Replicator 2), you'll have a small plastic shape!

That's it! If we leave off the mesh setup, let's call it 12 lines of code, to convert a mesh to GCode. 

I mentioned a GCode viewer above. If you would like to see your GCode paths, the gsSlicerApps solution also includes a project called SliceViewer. This is a GTKSharp app that uses SkiaSharp for 2D vector graphics drawing. Both of these open-source libraries are also cross-platform, I use this app regularly on Windows and OSX. 

I also use this project for active development of gsSlicer, so by default SliceViewer will usually be loading and slicing one of the included sample files on startup. However, if you drag-and-drop a .gcode file onto the window, SliceViewer will use gsGCode to parse it and extract the layer path geometry, which you can scan through using the up/down arrow keys.

Implicit Surface Modeling

[Update July 6, 2018] My new tool Cotangent has several Tools that use the operations I describe below, if you want to try them without writing C# code. Find then under Shell/Hollow, VoxWrap, VoxBoolean, VoxBlend, and Morphology [/EndUpdate]

In my previous post on Signed Distance Fields, I demonstrated ways to create a watertight surface around a set of input meshes. The basic strategy was, append all the meshes to a single mesh, and then create an SDF for the entire thing. That post led user soraryu to ask if it was possible to do this in a more structured and efficient way, where one could create separate per-mesh SDFs and then combine them. Not only is this possible, but taking this approach opens up quite a wide space of other modeling operations. In this post I will explain how this kind of modeling - called Implicit Modeling - works.

The first thing we need to do is understand a bit more about the math of SDFs. Remember, SDF means Signed Distance Field. Lets break this down. Distance in this context is the distance to the surface we are trying to represent. Field here means, it's a function over space, so at any 3D point p we can evaluate this function and it will return the distance to the surface. We will write this as F(p) below - but don't worry, the math here is all going to be straightforward equations. Finally, Signed means the distance will either be positive or negative. We use the sign to determine if p is inside the surface. The standard convention is that Negative == inside and Positive == outside. The surface is at distance == 0, or F(p) = 0. We call this an Implicit Surface because the surface is not explicitly defined - the equation doesn't tell us where it is. Instead we have to find it to visualize it (that's what the MarchingCubes algorithm does).

Lets forget about an arbitrary mesh for now and consider a simpler shape - a Sphere. Here is the code that calculates the signed distance to the surface of a sphere:

public double Value(Vector3d pt)
{
    return (pt-Center).Length - Radius;
}

So, this code is the function F(p) - sometimes we call this the "field function". You can evaluate it at any 3D point p, and the result is the signed distance to the sphere. The image to the right shows a "field image", where we sampled the distance field on a grid and converted to pixels. In fact, it's actually a 2D slice through the 3D sphere distance field. Here the (unsigned) distance value has been mapped to grayscale, and the zero values are red. 

In the case of a sphere, the SDF is analytic, meaning we can just calculate it directly. You can write an analytic SDF for many simple shapes. The current g3Sharp code includes ImplicitSphere3d, ImplicitAxisAlignedBox3d, ImplicitBox3d, ImplicitLine3d, and ImplicitHalfSpace3d (that's a plane).

If you look at the Value() functions for these classes you will see that they are all relatively simple. Íñigo Quílez has the code for a bunch of other analytic SDF shapes (he calls them "distance functions"). The same math I will explain on this page can be used with realtime GPU raytracing, which is pretty cool. You can check out his Shadertoy demo of these shapes as well, and here's one of mine based on his code.

For a Mesh, doing an analytic distance evaluation is possible (using DMesh3AABBTree, for example), but it is quite expensive if there are lots of triangles. So when using Mesh SDFs we usually sample the distance values on a grid (just like the pixel image), and then interpolate between the sampled values. This is exactly what we did in the previous tutorial - MeshSignedDistanceGrid did the sample-to-grid and then DenseGridTrilinearImplicit did the interpolation. 

Boolean Operators

If you just wanted to make some basic 3D shapes, using the SDF form and then running MarchingCubes to mesh them, is not particularly efficient. The big advantage of SDFs is that you can easily combine shapes represented in SDF form by mathematically combining the SDF functions. A function that takes in one or more input SDFs, and generates an output SDF, is called an Operator. 

View fullsize

The simplest compositions you can do with SDFs are the Boolean Operators Union, Intersection, and Difference. This is the complete opposite of meshes, where a mesh Boolean is incredibly difficult. With SDFs, Booleans are trivial to implement and always work (although you still have to mesh them!). The functions for the Boolean Operators are shown on the right. These are really just logical operations. Consider the Union, which is just the min() function. If you have two values, one less than 0 (inside) and one greater than 0 (outside), and you want to combine the two shapes, then you keep the smaller value. 

The code below generates the three meshes shown in the figure on the right. Here the SDF primitives are a sphere and a box. From left to right we have Union, Difference, and Intersection. In this code we are using a function generateMeshF, you will find that function at the end of this post. It is just running MarchingCubes and writing the mesh to the given path.

ImplicitSphere3d sphere = new ImplicitSphere3d() {
    Origin = Vector3d.Zero, Radius = 1.0
};
ImplicitBox3d box = new ImplicitBox3d() {
    Box = new Box3d(new Frame3f(Vector3f.AxisX), 0.5*Vector3d.One)
};

generateMeshF(new ImplicitUnion3d() { A = sphere, B = box }, 128, "c:\\demo\\union.obj");
generateMeshF(new ImplicitDifference3d() { A = sphere, B = box }, 128, "c:\\demo\\difference.obj");
generateMeshF(new ImplicitIntersection3d() { A = sphere, B = box }, 128, "c:\\demo\\intersection.obj");

We are using Binary Operators in this sample code. g3Sharp also includes N-ary operators ImplicitNaryUnion3d and ImplicitNaryDifference3d. These just apply the same functions to sets of inputs. 

Offset Surfaces

The Offset Surface operator is also trivial with SDFs. Remember, the surface is defined by distance == 0. If we wanted the surface to be shifted outwards by distance d, we could change the definition to distance == d. But we could also write this as (distance - d) == 0, and that's the entire code of the Offset Operator.

View fullsize

Just doing a single Offset of a Mesh SDF can be quite a powerful tool. The code below computes the inner and outer offset surfaces of the input mesh. If you wanted to, for example, Hollow a mesh for 3D printing, you can compute an inner offset at the desired wall thickness, flip the normals, and append it to the input mesh. 

double offset = 0.2f;
DMesh3 mesh = TestUtil.LoadTestInputMesh("bunny_solid.obj");
MeshTransforms.Scale(mesh, 3.0 / mesh.CachedBounds.MaxDim);
BoundedImplicitFunction3d meshImplicit = meshToImplicitF(mesh, 64, offset);

generateMeshF(meshImplicit, 128, "c:\\demo\\mesh.obj");
generateMeshF(new ImplicitOffset3d() { A = meshImplicit, Offset = offset }, 128, "c:\\demo\\mesh_outset.obj");
generateMeshF(new ImplicitOffset3d() { A = meshImplicit, Offset = -offset }, 128, "c:\\demo\\mesh_inset.obj");

This code uses a function meshToImplicitF, which generates the Mesh SDF using the code from the Mesh SDF tutorial. I included this function at the end of the post.

Smooth Booleans

View fullsize

So far, we have only applied Operators to input Primitives. But we can also apply an Operator to another Operator. For example this code applies Offset to the Union of our sphere and box:

var union = new ImplicitUnion3d() { A = sphere, B = box };
generateMeshF(new ImplicitOffset3d() { A = union, Offset = offset }, 128, "c:\\demo\\union_offset.obj");

Now you could plug this Offset into another Operator. Very cool! 

But, there's more we can do here. For example, what if we wanted this offset to have a smooth transition between the box and the sphere? The Min operator we use for the Boolean, has a discontinuity at the points where the two input functions are equal. What his means is, the output value abruptly "jumps" from one function to the other. Of course, this is what should happen on the surface, because a Boolean has a sharp transition from one shape to another. But it also happens in the "field" away from the surface. We don't see that field, but it affects the output of the Offset operation. 

We can create a field that has a different shape by using a different equation for the Union operator. We will use the form on the right. If either A or B is zero, this function will still return the other value, so it still does a Min/Max operation. But if both values are non-zero, it combines them in a way that smoothly varies between A and B, instead of the sharp discontinuous jump.

View fullsize

Here's some sample code that generates our Offset example with this "SmoothUnion". The original box/sphere union looks the same, however in the Offset surface, the transition is smooth. This is because the 

var smooth_union = new ImplicitSmoothDifference3d() { A = sphere, B = box };
generateMeshF(smooth_union, 128, "c:\\demo\\smooth_union.obj");
generateMeshF(new ImplicitOffset3d() { A = smooth_union, Offset = 0.2 }, 128, "c:\\demo\\smooth_union_offset.obj");

In this next section we will build on this SmoothUnion Operator, but first we need to cover one caveat. As I said above, if A and B are both non-zero, then this function produces a smooth combination of the input values. That's why we don't get the sharp transition. So, as you might expect, when we use d as the parameter to Offset, the offset distance in this smooth area cannot actually be d. 

View fullsize

However, this smooth-composition happens everywhere in space, not just around the transition. As a result, the actual offset distance is affected everwhere as well. The figure on the right shows the original shape, then the discontinuous Offset, and finally the Smooth Offset. You can see that even on the areas that are "just sphere" and "just box", the Smooth Offset is a little bit bigger.

This is the price we pay for these "magic" smooth Operators. We gain continuity but we lose some of the nice metric properties. Mathematically, this happens because the the SmoothUnion operator produces a field that has properties similar to a Distance Field, but it's not actually a Distance Field. Specifically, it's not normalized, meaning if you computed the gradient and took it's magnitude, it would not be 1. 

SmoothUnion is not just for shapes - it is called an R-Function, and R-functions implement Boolean logic using continuous functions, which has other applications. If this sounds interesting, here are a few starting points for further reading: [Shapiro88] [Shapiro07].

Blending Operator

By applying Offset to the SmoothUnion Operator, we can get a smooth transition in the offset surface. But what if we wanted that smooth transition between the input shapes, without the Offset? This is called a Blend Operator and is one of the biggest advantages of Implicit Modeling. 

We will build Blend off of SmoothUnion. Basically, we want to vary the offset distance, so that if the point is close to both the input surfaces, we offset, and if it's only close to one of them, we don't. This variation needs to be smooth to produce a continuous blend. We use the equation above, based on [Pasko95], and implemented in ImplicitBlend3d. Here is an example, followed by the resulting blended spheres.

ImplicitSphere3d sphere1 = new ImplicitSphere3d() {
    Origin = Vector3d.Zero, Radius = 1.0
};
ImplicitSphere3d sphere2 = new ImplicitSphere3d() {
    Origin = 1.5 * Vector3d.AxisX, Radius = 1.0
};
generateMeshF(new ImplicitBlend3d() { A = sphere1, B = sphere2, Blend = 1.0 }, 128, "c:\\demo\\blend_1.obj");
generateMeshF(new ImplicitBlend3d() { A = sphere1, B = sphere2, Blend = 4.0 }, 128, "c:\\demo\\blend_4.obj");
generateMeshF(new ImplicitBlend3d() { A = sphere1, B = sphere2, Blend = 16.0 }, 128, "c:\\demo\\blend_16.obj");
generateMeshF(new ImplicitBlend3d() { A = sphere1, B = sphere2, Blend = 64.0 }, 128, "c:\\demo\\blend_64.obj");

View fullsize

Mathematically, this blend is only C1 continous. As a result, although the surface is smooth, the variation in the normal is not. There are higher-order blending functions in [Pasko95], but they are computationally more intensive. Another aspect of this blend is that it has 3 parameters - w_blend, w_a, and w_b. Each of these affects the shape. In addition, the way they affect the shape depends on the scale of the distance values. In the example above, we used w_blend = 1,4,16,64. Each sphere had radius=1. If we use the same blending power with radius=2, we get different results:

It is possible to try to normalize w_blend based on, say, the bounding box of the input primitives. But, the per-shape weights w_a and w_b also come into play. If one shape is much smaller than the other, generally the larger one will "overwhelm" the smaller. You can use these weights to manipulate this effect. But changing these weights, also changes how much the blend surface deviates from the input surfaces in regions that are far from the places we would expect to see a blend. 

Does this all sound complicated? It is! This is the trade-off with Implicit Modeling. We can have almost trivial, perfectly robust Booleans, Offsets, and Blending, but our tools to precisely control the surface are limited to abstract weights and functions. It is possible to, for example, vary the blending weights over space [Pasko05], based on some other function, to provide more control. Mathematically this is all pretty straightforward to implement, much easier than even a basic Laplacian mesh deformation. But, the fact that you can't just grab the surface and tweak it, tends to make Implicit Modeling difficult to use in some interactive design tools.

Mesh Blending

View fullsize

Lets apply our Blend Operator to some Mesh SDFs. The image on the right is produced by this sample code. As you can see, something has gone quite wrong...

DMesh3 mesh1 = TestUtil.LoadTestInputMesh("bunny_solid.obj");
MeshTransforms.Scale(mesh1, 3.0 / mesh1.CachedBounds.MaxDim);
DMesh3 mesh2 = new DMesh3(mesh1);
MeshTransforms.Rotate(mesh2, mesh2.CachedBounds.Center, Quaternionf.AxisAngleD(Vector3f.OneNormalized, 45.0f));

var meshImplicit1 = meshToImplicitF(mesh1, 64, 0);
var meshImplicit2 = meshToImplicitF(mesh2, 64, 0);
generateMeshF(new ImplicitBlend3d() { A = meshImplicit1, B = meshImplicit2, Blend = 0.0 }, 128, "c:\\demo\\blend_mesh_union.obj");
generateMeshF(new ImplicitBlend3d() { A = meshImplicit1, B = meshImplicit2, Blend = 10.0 }, 128, "c:\\demo\\blend_mesh_bad.obj");

What happened? Well, we didn't cover this in the Mesh SDF tutorial, but now we can explain a bit more about what MeshSignedDistanceGrid does. Remember, it samples the Distance Field of the input Mesh. But, samples it where? If we want to just mesh the SDF, we don't need the precise distance everywhere, we just need it near the surface. So, by default, this class only computes precise distances in a "Narrow Band" around the input mesh. Values in the rest of the sample grid are filled in using a "sweeping" technique that only sets the correct sign, not the correct distance. The ridges in the above image show the extent of the Narrow Band. 

View fullsize

To get a better blend, we need to compute a full distance field, and the sampled field needs to extend far enough out to contain the blend region. This is much more expensive. The MeshSignedDistanceGrid class still only computes exact distances in a narrow band, but it will use a more expensive sweeping method which propagates more accurate distances. This is sufficient for blending. The meshToBlendImplicitF function (code at end of post) does this computation, and you can see the result of the sample code below on the right.

var meshFullImplicit1 = meshToBlendImplicitF(mesh1, 64);
var meshFullImplicit2 = meshToBlendImplicitF(mesh2, 64);
generateMeshF(new ImplicitBlend3d() { A = meshFullImplicit1, B = meshFullImplicit2, Blend = 1.0 }, 128, "c:\\demo\\blend_mesh_1.obj");
generateMeshF(new ImplicitBlend3d() { A = meshFullImplicit1, B = meshFullImplicit2, Blend = 10.0 }, 128, "c:\\demo\\blend_mesh_10.obj");
generateMeshF(new ImplicitBlend3d() { A = meshFullImplicit1, B = meshFullImplicit2, Blend = 50.0 }, 128, "c:\\demo\\blend_mesh_100.obj");

Lattice Demo

View fullsize

In the Mesh SDF post, I created a lattice by generating elements for each mesh edge. Now that we have these Primitives and Operators, we have some alternative ways to do this kind of thing. If we  first Simplify our bunny mesh using this code:

DMesh3 mesh = TestUtil.LoadTestInputMesh("bunny_solid.obj");
MeshTransforms.Scale(mesh, 3.0 / mesh.CachedBounds.MaxDim);
MeshTransforms.Translate(mesh, -mesh.CachedBounds.Center);
Reducer r = new Reducer(mesh);
r.ReduceToTriangleCount(100);

And then use this following code to generate Line Primitives for each mesh edge and Union them:

double radius = 0.1;
List<BoundedImplicitFunction3d> Lines = new List<BoundedImplicitFunction3d>();
foreach (Index4i edge_info in mesh.Edges()) {
    var segment = new Segment3d(mesh.GetVertex(edge_info.a), mesh.GetVertex(edge_info.b));
    Lines.Add(new ImplicitLine3d() { Segment = segment, Radius = radius });
}
ImplicitNaryUnion3d unionN = new ImplicitNaryUnion3d() { Children = Lines };
generateMeshF(unionN, 128, "c:\\demo\\mesh_edges.obj");

View fullsize

The result is an Analytic implicit 3D lattice. Now, say we wanted to strengthen the junctions.
We can just add in some spheres, and get the result on the right:

radius = 0.05;
List<BoundedImplicitFunction3d> Elements = new List<BoundedImplicitFunction3d>();
foreach (int eid in mesh.EdgeIndices()) {
    var segment = new Segment3d(mesh.GetEdgePoint(eid, 0), mesh.GetEdgePoint(eid, 1));
    Elements.Add(new ImplicitLine3d() { Segment = segment, Radius = radius });
}
foreach (Vector3d v in mesh.Vertices())
    Elements.Add(new ImplicitSphere3d() { Origin = v, Radius = 2 * radius });
generateMeshF(new ImplicitNaryUnion3d() { Children = Elements }, 256, "c:\\demo\\mesh_edges_and_vertices.obj");

Lightweighting Demo

View fullsize

Lightweighting in 3D printing is a process of taking a solid shape and reducing its weight, usually by adding hollow structures. There are sophisticated tools for this, like nTopology Element. But based on the tools we have so far, we can do some basic lightweighting in just a few lines of code. In this section we will hollow a mesh and fill the cavity with a grid pattern, entirely using Implicit modeling. The result is shown on the right (I cut away part of the shell to show the interior).

First we have a few parameters. These define the spacing of the lattice elements, and the wall thickness. This code is not particularly fast, so I would experiment using a low mesh resolution, and then turn it up for a nice result (and probably Reduce if you are planning to print it!).

double lattice_radius = 0.05;
double lattice_spacing = 0.4;
double shell_thickness = 0.05;
int mesh_resolution = 64;   // set to 256 for image quality

This is a bit of setup code that creates the Mesh SDF and finds the bounding boxes we will need

var shellMeshImplicit = meshToImplicitF(mesh, 128, shell_thickness);
double max_dim = mesh.CachedBounds.MaxDim;
AxisAlignedBox3d bounds = new AxisAlignedBox3d(mesh.CachedBounds.Center, max_dim / 2);
bounds.Expand(2 * lattice_spacing);
AxisAlignedBox2d element = new AxisAlignedBox2d(lattice_spacing);
AxisAlignedBox2d bounds_xy = new AxisAlignedBox2d(bounds.Min.xy, bounds.Max.xy);
AxisAlignedBox2d bounds_xz = new AxisAlignedBox2d(bounds.Min.xz, bounds.Max.xz);
AxisAlignedBox2d bounds_yz = new AxisAlignedBox2d(bounds.Min.yz, bounds.Max.yz);

View fullsize

Now we make the 3D lattice. Note that we are making a full 3D tiling here, this has nothing to do with the input mesh shape. The image on the right shows what the lattice volume looks like. The code is just creating a bunch of line Primitives and then doing a giant Union.

List<BoundedImplicitFunction3d> Tiling = new List<BoundedImplicitFunction3d>();
foreach (Vector2d uv in TilingUtil.BoundedRegularTiling2(element, bounds_xy, 0)) {
    Segment3d seg = new Segment3d(new Vector3d(uv.x, uv.y, bounds.Min.z), new Vector3d(uv.x, uv.y, bounds.Max.z));
    Tiling.Add(new ImplicitLine3d() { Segment = seg, Radius = lattice_radius });
}
foreach (Vector2d uv in TilingUtil.BoundedRegularTiling2(element, bounds_xz, 0)) {
    Segment3d seg = new Segment3d(new Vector3d(uv.x, bounds.Min.y, uv.y), new Vector3d(uv.x, bounds.Max.y, uv.y));
    Tiling.Add(new ImplicitLine3d() { Segment = seg, Radius = lattice_radius });
}
foreach (Vector2d uv in TilingUtil.BoundedRegularTiling2(element, bounds_yz, 0)) {
    Segment3d seg = new Segment3d(new Vector3d(bounds.Min.x, uv.x, uv.y), new Vector3d(bounds.Max.x, uv.x, uv.y));
    Tiling.Add(new ImplicitLine3d() { Segment = seg, Radius = lattice_radius });
}
ImplicitNaryUnion3d lattice = new ImplicitNaryUnion3d() { Children = Tiling };
generateMeshF(lattice, 128, "c:\\demo\\lattice.obj");

These two lines Intersect the lattice with the Mesh SDF, clipping it against the input mesh. If you just wanted the inner lattice, you're done!

ImplicitIntersection3d lattice_clipped = new ImplicitIntersection3d() { A = lattice, B = shellMeshImplicit };
generateMeshF(lattice_clipped, mesh_resolution, "c:\\demo\\lattice_clipped.obj");

Now we make the shell, by subtracting an Offset of the Mesh SDF from the original Mesh SDF. Finally, we Union the shell and the clipped lattice, to get out result

var shell = new ImplicitDifference3d() {
    A = shellMeshImplicit, 
    B = new ImplicitOffset3d() { A = shellMeshImplicit, Offset = -shell_thickness }
};
generateMeshF(new ImplicitUnion3d() { A = lattice_clipped, B = shell }, mesh_resolution, "c:\\demo\\lattice_result.obj");

That's it! If you wanted to, say, print this on a Formlabs printer, you might want to add some holes. This is easily done using additional operators. I'll leave it as an excerise to the reader =)

Ok, that's it. The remaining code is for the generateMeshF, meshToImplicitF, and meshToBlendImplicitF functions. Good luck!

// generateMeshF() meshes the input implicit function at
// the given cell resolution, and writes out the resulting mesh    
Action<BoundedImplicitFunction3d, int, string> generateMeshF = (root, numcells, path) => {
    MarchingCubes c = new MarchingCubes();
    c.Implicit = root;
    c.RootMode = MarchingCubes.RootfindingModes.LerpSteps;      // cube-edge convergence method
    c.RootModeSteps = 5;                                        // number of iterations
    c.Bounds = root.Bounds();
    c.CubeSize = c.Bounds.MaxDim / numcells;
    c.Bounds.Expand(3 * c.CubeSize);                            // leave a buffer of cells
    c.Generate();
    MeshNormals.QuickCompute(c.Mesh);                           // generate normals
    StandardMeshWriter.WriteMesh(path, c.Mesh, WriteOptions.Defaults);   // write mesh
};

// meshToImplicitF() generates a narrow-band distance-field and
// returns it as an implicit surface, that can be combined with other implicits                       
Func<DMesh3, int, double, BoundedImplicitFunction3d> meshToImplicitF = (meshIn, numcells, max_offset) => {
    double meshCellsize = meshIn.CachedBounds.MaxDim / numcells;
    MeshSignedDistanceGrid levelSet = new MeshSignedDistanceGrid(meshIn, meshCellsize);
    levelSet.ExactBandWidth = (int)(max_offset / meshCellsize) + 1;
    levelSet.Compute();
    return new DenseGridTrilinearImplicit(levelSet.Grid, levelSet.GridOrigin, levelSet.CellSize);
};

// meshToBlendImplicitF() computes the full distance-field grid for the input 
// mesh. The bounds are expanded quite a bit to allow for blending,
// probably more than necessary in most cases    
Func<DMesh3, int, BoundedImplicitFunction3d> meshToBlendImplicitF = (meshIn, numcells) => {
    double meshCellsize = meshIn.CachedBounds.MaxDim / numcells;
    MeshSignedDistanceGrid levelSet = new MeshSignedDistanceGrid(meshIn, meshCellsize);
    levelSet.ExpandBounds = meshIn.CachedBounds.Diagonal * 0.25;        // need some values outside mesh
    levelSet.ComputeMode = MeshSignedDistanceGrid.ComputeModes.FullGrid;
    levelSet.Compute();
    return new DenseGridTrilinearImplicit(levelSet.Grid, levelSet.GridOrigin, levelSet.CellSize);
};

AWS Cognito User Account Signup And Login with Unity

Let's get this out of the way up front: If you are mostly interested in the 3D geometry things I do at gradientspace, this post is Not For You. Sorry!

Although I also prefer to do the 3D geometry, once in a while I need to do something else. And the thing I needed to do today (for a client project) was figure out how to use the Amazon AWS Cognito service to manage user accounts. The Cognito APIs let you implement things like user registration and log-in, password resets, and so on. And AWS has a very extensive .NET SDK, so you can do all these things from a C# mobile or desktop app.

Which sounds great. Except, there is a special Unity version of the AWS .NET SDK. And this specific thing I needed to do - Cognito Signup and Login - is not supported in the Unity version of the SDK. 

So, I made it work.

If you would also like to make it work, continue reading. If not, really, check out these awesome signed distance fields!

Step 1 - Update the AWS SDK

The AWS .NET SDK for Unity seems...wildly out-of-date. The documentation is going on and on about Unity 5, but Unity doesn't even have version numbers anymore. Unity 2017 was released 6 months ago! So, this thing, it's kind of broken. Luckily, it's also open-source - right there on github. Although it's not clearly documented, the entire SDK is auto-generated, and so making large-scale changes just requires tweaks to a few template files. It was a one-character change to have the generator output visual studio projects for .NET 4.5 instead of .NET 3.5 (you're not still using .NET 3.5, are you? gross!). It was also not linking to the new split UnityEngine.dll system. These are fixed in the few commits I added to my fork of the project.

The other nice thing about this auto-generator is that adding the CognitoIdentityProvider service - the thing that is missing from the Unity SDK - was pretty straightforward. I can't say I really understand how it all works. But, there are some config files, you cut here, paste there, run the generator, and voila - it's in the Unity build. 

So, if you want to make your own Unity 2017.3 .NET 4.5 dlls, you can grab my fork, open sdk\AWSSDK.Unity.sln, and build all. Somebody else can figure out how to make it spit out the .unitypackage file, I just collected up the DLLs I needed manually from the bin\Release subfolders.

Step 2 - AWS User Pool Configuration

So, building the CognitoIdentityProvider for Unity turned out to be pretty easy. Using it? Not so much. Even using it in non-Unity "supported" .NET is a bit of a mess, based on the hundreds of confused developers you will find in your Googles. So, I have prepared for you a fully functional Unity project - it is here also on github. Open this project in Unity, and, after you configure your AWS appropriately, it should allow you to register a Cognito user account, as well as sign in and get those delicious tokens. At least, it did today, July 25 2018, on my Windows 10 computer with Unity 2017.3.0f3. Tomorrow, who could say? This is the world we have created for ourselves.

First you need to configure your Cognito User Pool appropriately. If you are reading this, you probably already know what a User Pool is. If not, the AWS Docs have a pretty good walkthrough of this, but there are a few critical settings you will need to know about. At some point in this setup, you are going to create an App Client and associate it with your User Pool. It will look like the screen on the right. By default, Generate client secret is checked. Un-check it!

If you don't do this, then AWS will generate and associate a secret key with this app client, and for each request you will have to combine this key with some other math things to create a hash. You'll be able to get this to work for the Signup request, because the request object it has a field for the hash. But, the Sign-in request does not. You can't change this setting after you create the App Client (but you can create multiple App Clients for a given User Pool, if you already have a User Pool you don't want to throw away)

Two other things. By default, email verification for your user pool will be enabled, but instead of sending an email verification link, it will send a numeric code. I have no idea what the user would do with this code. But, you can change it to email a clickable link instead. After you have created the user Pool, go to the Message Customizations page and change Verification Type to Link. 

Finally, you can set a domain for your App Client as well. You will find this in the the Domain Name page (one of the links in the left bar of the User Pool page).  Once you set that, you can actually go to this URL in a browser, and if you View Source, it looks like maybe this is a page to sign up and/or manage accounts. However, the page only renders a blank white background. Confusing. But until I did this, I got an exception when signing up for accounts. 

Step 3 - Unity!

You are almost there. Open my Unity sample project. Open the C# project. Open the CognitoThings.cs file. You will find this at the top:

This is the AWS Configuration strings you need to set up before you can talk to AWS. Note that this is much simpler than some other AWS things you might want/need to do, because there are no secret keys involved. The Cognito Signup/Login APIs do not need any secret keys, which is great because these are a pain to handle safely in Unity. The code comments tell you were to find everything. Note that the UserPoolName is a substring of UserPoolID. Don't forget to set the right RegionEndpoint.

Once you have set the magic strings, you are ready. Open the scene named CognitoTestScene. Hit Play. You will see an ugly form. Enter an email address and a password (that complies with the password policy you set in your User Pool. Don't remember? The default is lower and upper case, a number, and a symbol). Hit Signup. 

If it worked, you will get a confirmation email. Once you confirm, you can then click Sign in and see the first few characters of one of the authentication tokens that AWS returned. If you jump over to the Users and Groups page in the User Pool page of the AWS Console, you should see your new account listed as CONFIRMED.

It is a bit difficult to delete Cognito user accounts. You can't do it from the AWS management website, you have to use the command-line tools. But, you have to put in valid email addresses to test things. So, I found GMail's disposable address system to be helpful for testing.

Step X - The Code

If you are reading this post, it can only possibly be that you need/want to develop something that uses Cognito User Accounts (otherwise, why are you reading this? it is not interesting.) So, as far as the code goes, all the good stuff is in the CognitoThings Monobehavior. There are really only 2 functions, TrySignupRequest() and TrySignInRequest(). The Signup request is relatively simple, you just send the username and password (I may be mistaken, but it seems like this password is sent as plaintext. Hrm...).

The Sign-in is...complicated. Basically, you do not just send a username and password "over the wire" to AWS because that is a bad idea, security-wise. Even if you would really like to do it just this one time and promise to never ship it, it is not supported. Instead what you do is, you construct some math numbers, send them, and then AWS does more math things and sends back some other numbers, that you combine (irreversibly) with the password and send back a second time. AWS checks your math, and if it adds up, it is convinced that you know the password it has on file, without you ever having to send the password. Cryptography! it's wild. 

But, oddly, doing all this math stuff is not actually part of the AWS .NET SDK, and is in fact quite difficult to implement. AWS has released a developer preview of a library that handles this - but not for Unity. Let's hope that materializes soon? Luckily, Markus Lachinger has an excellent blog post about it, and standalone .NET sample code for Cognito Sign-in that I borrowed liberally from to make this work. Most of his code is in CognitoAuthUtil.cs, which handles computation of the math numbers. This code uses an open-source library called BouncyCastle from Australia (Australia!). I have included a compiled BouncyCastle.dll, you can make your own from their github repo if you prefer.

The two functions TrySignupRequest and TrySignInRequest take callback functions for success and error, however these have no arguments. In cases of failure, you will need to dive into the response objects yourself and decide what to do. Similarly, when the Sign In succeeds, you get an instance of AuthenticationResultType that contains the ID, Access, and Refresh tokens. You'll have to work out what to do with these yourself - here is an explanation of what they are for.

Ok, I hope I have saved you some suffering. Unless you read this far but aren't going to use it - then I apologize for the suffering I have caused.

DMesh3: A Dynamic Indexed Triangle Mesh

If you are using the g3Sharp library, there is a good chance it's because you need to do some things with triangle meshes. If so, then the triangle mesh data structure is kind of important! In g3Sharp, this is the DMesh3 class. In this post I will dive into the details of this data structure and the operations it provides. Along the way I will try to explain some of the central concepts of triangle mesh data structures, which should also apply to other triangle mesh libraries.

At its core, DMesh3 is an index-based triangle mesh. This means that we reference components of the mesh - ie the vertices and triangles - by integer indices, rather than pointers. This is similar to the basic mesh data structures used in many other libraries. For example, Unity's Mesh class is also an indexed mesh, and the vertex buffers you might pass to a low-level graphics API like OpenGL/Direct3D/Vulkan/Metal are indexed meshes. The diagram below shows how these things connect up. Each vertex is a triplet or 3-tuple of real values (x,y,z) which are the 3D coordinates. In DMesh3 we store these in double-precision floating point. Then, each triangle is an integer 3-tuple (a,b,c), where each integer is the index of one of the vertices.

View fullsize

For many mesh processing tasks, this is all we really need. For example to render the triangles we just need the vertices of each triangle. If we want to estimate vertex normals, we can iterate over the triangles and accumulate their facet normals at the vertices. If we want to animate the mesh, we can modify the vertices. We can do a lot with just the basic indexed mesh, and it is the most memory-efficient mesh representation. The SimpleMesh class stores a mesh in this format.

But what if we want to know which triangles are connected to a specific vertex, or find the triangles connected to a specific triangle? These are common tasks in mesh processing. Even for something as basic as deleting a set of vertices, we'll need to find the list of affected faces. Of course we can compute this information from the triangle indices - this is called the adjacency graph, and we frequently refer to it as part of the mesh topology. However, computing the adjacency graph takes time, and in g3Sharp we use it often enough that we want to just keep it around all the time. So, we will add it directly into our mesh data structure.

First, we will explicitly represent the edges of the mesh. In a manifold triangle mesh, each edge has a vertex at either end, and is connected to one or two triangles (if it's just one, then this edge is on an open boundary of the mesh). So each edge is a 4-tuple (v₀, v₁, t₀, t₁), where if the edge is a boundary edge, then t₁ will be set to the invalid index (which is -1, but you should use the constant DMesh3.InvalidID). These edges connect up pairs of vertices and faces, but we still need to know how to get from vertices to edges. So, for each vertex, DMesh3 stores a list of connected edges. The diagrams below illustrate this connectivity.

View fullsize

Storing the set of edges connected to a vertex adds a significant complication, because the number of edges is variable. At the implementation level, this means we need dynamically-sized per-vertex lists, which we will discuss further below. But at the conceptual level, we have largely solved our connectivity problems. If we have a vertex and want to find the set of faces it connects to - we call this it's one-ring - we can iterate over the edges, and collect up the unique triangle indices. If we would like to find the edge between two vertices A and B, we can just iterate over the edges at A and search for the one that connects to vertex B. 

However, because of this variable-sized list, some common tasks are still relatively expensive. In particular, consider finding the three neighbour triangles for a given triangle. This involves iterating over each edge one-ring of each of the vertices of the triangle. When we manipulate regions of selected triangles, we need to do this search for each triangle in the selection, often many times, and so this search overhead is significant. 

We can avoid these searches by explicitly storing the triplet of edges (e_ab, e_bc, e_ca) for each triangle, as shown in the diagram below.

View fullsize

View fullsize

Storing the triangle edges in this way is redundant. However it vastly simplifies many algorithms, and we find it to be worth the memory cost. For example, although one can find the edge between vertices A and B using the list-search described above, if A and B come from a known triangle, then the edge can be found in constant time. This is also a very frequent operation in many mesh processing algorithms. 

Accessors and Internal Storage

The DMesh3 class provides interfaces for accessing the above elements. For example, GetVertex(vi) returns (x,y,z) for a given vertex index, and GetTriangle(ti) returns the (a,b,c) tuple. For edges, GetEdgeV(ei) returns the two edge vertices, GetEdgeT(ei) returns the triangles, and GetEdge(ei) returns both in a 4-tuple Index4i struct. FindEdge(a,b) returns the index of the edge between a and b, while FindEdgeFromTri(a,b,ti) uses the more efficient triangle-based query described above. 

Similarly, convenient iterations are provided like VtxVerticesItr(vi) to iterate over the vertices connected to vertex vi, as well as VtxEdgesItr(vi) and VtxTrianglesItr(vi). The GetTriEdges(ti) function returns the triangle-edge triplet, while GetTriNeighbourTris(ti) returns the neighbour triangles, and TriTrianglesItr(ti) provides the same values via an IEnumerable<int>. So, you can iterate over an edge-one ring like so:

foreach (int eid in mesh.VtxEdgesItr(vid)) {
    //....
}

There are also various task-specific queries that are useful in certain situations. For example, GetVtxNbrhood(eid,vid) looks up the "other" vertex of edge eid, as well as the connected triangles and "opposing" vertices, which are needed to compute the cotangent weights used in Laplacian mesh processing. You can of course compute this yourself using the above functions, but DMesh3 can do it more efficiently because it can directly query its internal data structures.

And what are these data structures, exactly? Most DMesh3 clients will not need to know, but it is relevant in some situations, so I will describe it in detail here. DMesh3 stores its indexable lists using the DVector<T> class. This class provides an array/list-like interface, ie the i'th element of type T can be accessed as array[i], and set as array[i] = v. However, internally the elements are not stored in a single contiguous array. Instead, DVector allocates memory in blocks, and the index accessor maps between the external linear index and the internal block/index pair. 

View fullsize

In the current DVector implementation, each block is 2048 items. This is a hardcoded value to optimize indexing via bitwise operations. If you profile g3Sharp code, you will often find that DVector.this[] is the top hotspot, called via many DMesh3 functions. This is why DMesh3 stores the redundant triangle edges, and provides many variations on its accessor functions - because these allow us to minimize unnecessary queries that, when done millions of times, can really add up!

Why use a DVector instead of a C# List? The main reason is to avoid allocating huge linear blocks of memory. A triangle mesh can easily involve millions of elements, which means the internal buffers would be very large. In addition, if the mesh is growing - for example when adding triangles - the C# List class will resize itself multiple times, which means new allocations and buffer-copies. In interactive applications this can result in noticeable pauses. With DVector this situation never occurs. 

If you look inside DMesh3, you may note that rather than the vertices list being a DVector<Vector3d>, it is instead a DVector<double>, and similarly for the triangles, edges, and so on. Because C# does not support returning references, it is not possible to use common C++ idioms that would allow for more efficient access. Frankly, in C# storing structs inside a list is risky, and a common source of errors. In addition, by using POD types, we can directly serialize the DVector buffers, which can be useful in interop situations. However, this is a design decision that is largely encapsulated inside DMesh3 and may be revisited in the future.

Vertex Edge Lists

As I mentioned above, the variable-length per-vertex edge lists are a significant complication. For a small mesh, using a List<int> for each vertex is not outrageous, but if we have millions of vertices, then we have millions of tiny lists and this starts to become a problem. In particular, if we are changing the mesh, we will be updating these lists and so even more memory allocations (and garbage collections) will occur. In fact the initial DMesh3 implementation used Lists and during something like a remeshing pass, the GC was constantly working to clean up all the List objects being generated and discarded.

To alleviate this, the per-vertex lists are represented by a SmallListSet object. This class is designed to store a large number of small integer lists, where we have a priori knowledge of how many elements will be in the median list. If the median list size is K, then each list begins with K contiguous elements (think "array", but they are not stored as separate Array objects). If the list grows larger than this, then we spill into additional elements stored via a linked-list, as shown in the diagram.

K should be set so that "most" lists fit in the initial block of elements. In a perfectly regular mesh each vertex is connected to 6 edges, but in the current implementation we set K = 8. This gives us some breathing room. Internally, SmallListSet is built out of DVector<int> instances, and even can re-use previously-allocated lists that have been freed. As a result, memory allocations due to the vertex_edge lists are very infrequent. In addition, this scheme is approximately 30% more space-efficient than per-vertex Lists. Although most vertices will not need the full 8 ints in the initial per-list array, we make it up on the overhead of managing all those separate C# objects.

Dynamic Mesh Operations

DMesh3 is not just an indexed triangle mesh - it is a dynamic indexed triangle mesh. This means that we can modify the mesh topology, for example by deleting triangles, splitting edges, and so on. This are complex operations because the data structures above must be updated to remain internally consistent. However, these are mainly internal issues. From the perspective of the user of DMesh3, the immediate complication is that, if we delete a triangle, its index is now invalid.

Internally, for each of the vertices, edges, and triangles lists, DMesh3 also stores a reference count for each index, implemented via a RefCountVector object. When a vertex is deleted, its reference count is set to an invalid value (currently -1), which indicates that this index is no longer in use. The RefCountVector also maintains a list of these free indices, and functions like AppendVertex() and AppendTriangle() will preferentially re-use free indices. The reference counts themselves are stored as 16-bit short integers, which limits the valence of a vertex to ~65k.

These are internal implementation details - you don't have to interact with the reference counts yourself.  However, it is critical to understand that after some mesh processing operations - like after Mesh Simplification via Reducer - a DMesh3 instance will have gaps in its index space, where certain indices will be invalid. If there are invalid indices, we say the mesh is Non-Compact, and DMesh3.IsCompact can be used to determine when this is the case. 

When the mesh is Non-Compact, you *cannot* blindly iterate from 0 to TriangleCount or VertexCount, because some indices are invalid. The functions IsVertex(vi), IsTriangle(ti), and IsEdge(ei) can be used to check if a given index is valid. However, for a Non-Compact mesh you also cannot rely on VertexCount and TriangleCount as an iteration boundary, because they return the number of valid indices, not the maximum index. If you take a mesh with a million triangles and delete all but 100 of them, it is entirely possible that one of the triangles has an index of 999999. So, to properly iterate via indices over a Non-Compact mesh you must iterate from 0 to MaxTriangleID or MaxVertexID. These values are the maximum allocated indices. 

If this all sounds inconvenient, you are strongly encouraged to instead always use the functions VertexIndices() and TriangleIndices(). These functions return IEnumerables that iterate over only the valid indices. 

In some situations, such as converting a processed DMesh3 to a different mesh format, you may wish to Compact the mesh, so that the index space is dense. The simplest way to do this is to use the compacting copy-constructor like so:

DMesh3 compactMesh = new DMesh3(noncompactMesh, true)

The resulting mesh will have indices that are tightly packed. Note that compacting is more computationally and memory intensive than non-compacting copies, because the internal buffers cannot be copied directly. So if you are doing a series of mesh processing operations, it is best to only compact at the end, or when necessary. If you need to know the mapping from old to new indices, you can use CompactCopy(), which returns a data structure containing these index maps. And CompactInPlace() can compact a given mesh without having to create a copy. However, if the mesh is large and even moderately sparse, this is more expensive than compacting with a copy.

Vertex Attributes and Triangle Groups

DMesh3 provides a few common per-vertex attribute buffers for vertex normals, colors, and uvs. The normals and colors are stored in single-precision floating point, and for the colors, only RGB values are available, there is no alpha channel. The UVs are stored as 2-element floats. 

These buffers are optional. By default they are not allocated. The various constructors and copy functions can enable these buffers at setup. You can also use functions like EnableVertexNormals(), etc, to initialize vertex attributes for a given mesh, and DiscardVertexNormals()/etc to throw them away. The DMesh3.Components property returns a MeshComponents enum-flags, which will tell you if a mesh has a particular buffer, as can the HasVertexColors/etc properties.

There is only one per-triangle attribute, an integer triangle group field. Usage of this is up to you. However we do use triangle groups inside g3Sharp to indicate semantic groupings of triangles. For example Remesher and Reducer can be configured to preserve the boundaries of sets of triangles with the same group.

Modification Operations

Since DMesh3 is dynamic, you can change it. There are various functions to do so, which properly update all the internal data structures to keep the mesh consistent. RemoveTriangle() and RemoveVertex() can be used to delete elements. SplitEdge(), CollapseEdge(), and FlipEdge() implement the standard mesh refinement operations. PokeTriangle() does a 1-to-3 triangle subdivision by adding a vertex at the triangle centroid.

The MergeEdges() function combines two edges into one. Conceptually this is performed by welding each pair of vertices. However a single vertex weld creates a bowtie vertex, so MergeEdges does both, and the mesh is never left in a non-manifold state. In addition, MergeEdges will properly close the zero-area holes that occur when, for example, merging the second-last of a pair of edge loops. 

These functions return a MeshResult enum, and for the more complex operations, also an operation-specific data structure like DMesh3.EdgeCollapseInfo. These structs provide information on what happened to the mesh - indices of elements removed and added, and so on. 

Metadata, Timestamps, Sanity Checks, and Serialization

DMesh3 has a few other capabilities that are useful in certain situations. In the extensibility direction, you can add arbitrary string/object pairs via AttachMetadata(), and look up said objects later using FindMetadata(). This is a bit of a hack, frankly, but it means that if absolutely necessary, you can attach data to a mesh as it is passed from one place to another. For example, when working with a custom mesh format, you can use AttachMetadata() to hang on to any format-specific mesh attribute data, without having to subclass or duplicate every mesh processing function you need to call. Note, however, that metadata is not copied/transferred by the DMesh3 copy constructors.

It is often useful to know if a mesh has changed. We find this happens frequently in interactive contexts, where we need to build caches/buffers to render a mesh, and we want to rebuild these caches if the mesh changes. Rather than events, DMesh3 has timestamps which are updated when the mesh is modified. These are not actually date/times, but rather just integers that are incremented on any mesh update. DMesh3.Timestamp is incremented when any mesh attribute changes, while DMesh3.ShapeTimestamp is only incremented when the mesh topology or shape changes (so, not when a vertex normal/color/uv or face group is updated).

Most of the functions in DMesh3, and the code in the rest of g3Sharp, assumes that the mesh is internally consistent - ie no valid triangle references invalid vertices, that sort of thing. However, particularly when loading mesh files or constructing them from external index buffers, this may not be the case. The function CheckValidity() can be used to verify that the mesh is well-formed. If you are encountering weird issues, it is a good idea to throw in a few calls to this function. Note that by default it will consider bowtie vertices to be invalid, this is configurable via the first argument and may not be desirable in certain contexts. 

The IsSameMesh() function will tell you if two meshes are "the same", and is useful primarily for testing. By default it only checks that the vertices and triangles are the same, checking of other mesh elements can be enabled with the many arguments.

Finally, if you need to serialize a DMesh3, you can use the functions gSerialization.Store() and gSerialization.Restore(). The restored mesh will preserve all vertex/triangle/edge indices and allocated vertex/triangle attributes. However if you don't care about these things, you can get a much more compact serialization by just storing the vertex coordinates and triangle indices yourself (although reconstructing the DMesh3 from the deserialized buffers will be more expensive).

Questions Answered

Why an indexed mesh?

Many mesh libraries that aim to support similar dynamic-mesh capabilities use pointer-based meshes, where a level of indirection allows for the "invalid-index" problem to be avoided. However, such approaches tend to not scale well to huge meshes. If each vertex and triangle is a full object, then the memory allocator must manage millions of tiny objects, which is not ideal. Other clever pointer-like schemes can be used, but if taken to the extremes of efficiency, the result is often essentially an indexed mesh, but without the advantages of being able to make assumptions about indices.

Having indices means we can iterate over them, or over subsets. Even when the index space has gaps, it can be beneficial to iterate over indices and simply test-and-skip invalid indices - particularly in multi-threaded code. An index iteration doesn't become invalid if we modify the mesh during an iteration. We can do math on indices, and serializing index-based data structures is much simpler. And finally, trying to debug pointer-based mesh code is sheer madness, in the author's humble opinion.

Is this a Winged-Edge Mesh?

No. Although DMesh3 edges do connect two vertices and have two adjacent faces, we do not store the other topological connectivity links common in Winged Edge meshes, and we do not guarantee anything about the ordering of faces. 

Why not Half-Edge?

Half-Edge mesh data structures have the advantage that all elements have fixed size, ie our per-vertex variable-sized list is not necessary. They also have other benefits, and are more efficient for various kinds of element-adjacency iterations. However, Half-Edge is generally a pointer-based mesh data structure, and so inherits some of the problems described above. In addition, half-edge mesh code, although conceptually elegant, can be quite difficult to read. 

Can DMesh3 store non-manifold meshes?

DMesh3 does allow for bowtie vertices, ie non-manifold vertices that are connected to more than two boundary edges. However, some functions in DMesh3 will fail to operate properly on edges connected to bowtie vertices, in particular CollapseEdge(). 

Non-manifold edges, where more than two faces meet at an edge, cannot be represented because the DMesh3 edge elements only reference two triangles. Functions like AddTriangle() will return an error if you try to add a non-manifold triangle. The NTMesh3 class is a variant of DMesh3 that can store non-manifold topology, however it currently does not have many of the other DMesh3 operations implemented. 

3D Bitmaps, Minecraft Cubes, and Mesh Winding Numbers

As a follow-up to my Signed Distance Fields tutorial, a reader asked about how to voxelize a mesh. The MeshSignedDistanceGrid that we computed is a kind of voxelization, but this reader was (I assume) asking about binary voxels - ie the blocky, minecraft-y kind - which can be represented with a Bitmap3 object, where each (i,j,k) entry is true if it is inside the mesh and false if it is outside.

There are several ways to create this Bitmap3 voxelization of a mesh. If you start with the MeshSignedDistanceGrid from the SDF Tutorial, then you can convert it to a binary bitmap like so:

// create SDF
MeshSignedDistanceGrid levelSet = ...

Bitmap3 bmp = new Bitmap3(levelSet.Dimensions);
foreach(Vector3i idx in bmp.Indices()) {
    float f = levelSet[idx.x, idx.y, idx.z];
    bmp.Set(idx, (f < 0) ? true : false);
}

This block creates a Bitmap3 with the same dimensions as the SDF, and then for each index, sets the voxel as "inside" (true) if the distance is negative. 

Creating a Minecraft-Style Surface Mesh

If you would like to see what the binary voxelization looks like, you can use the VoxelSurfaceGenerator class to create a Minecraft-style mesh of the voxel faces:

VoxelSurfaceGenerator voxGen = new VoxelSurfaceGenerator();
voxGen.Voxels = bmp;
voxGen.ColorSourceF = (idx) => {
    return new Colorf((float)idx.x, (float)idx.y, (float)idx.z) * (1.0f / numcells);
};
voxGen.Generate();
DMesh3 voxMesh = voxGen.Meshes[0];
Util.WriteDebugMesh(voxMesh, "your\\path\\mesh_file.obj");

View fullsize

Click to enlarge

The ColorSourceF function I am setting here is used to provide a solid color for each block. This is helpful for visualization, but might also be useful if for example you had some spatial coloring function you wanted to visualize. You can also assign colors to the mesh afterwards, of course.

The last line writes out the mesh to an OBJ file, you'll have to provide your own path. The result is shown to the right, for our standard bunny mesh. This image is a screen shot from Autodesk Meshmixer, with boundary edges shown in blue. Note that the mesh generated by VoxelSurfaceGenerator is actually a bunch of small squares, that are simply adjacent. So, many mesh processing techniques will not work on this mesh.

We could try to weld these borders together, but if we aren't careful this will result in non-manifold topology where more than two faces meet along an edge or at a vertex. We'll cover that in a future tutorial.

Voxelization with a Point-Containment Queries

Generating an SDF is one way to voxelize a mesh, and perhaps the fastest, because we only have to resolve inside/outside near the surface. A fast-sweeping algorithm is then used to fill the rest of space. However, we have some other options, which do have some benefits. Here is an alternative that uses DMeshAABBTree3.IsInside() to set the inside/outside value at each voxel:

DMesh3 mesh = (load mesh...);
DMeshAABBTree3 spatial = new DMeshAABBTree3(mesh, autoBuild: true);

AxisAlignedBox3d bounds = mesh.CachedBounds;
int numcells = 32;
double cellsize = bounds.MaxDim / numcells;
ShiftGridIndexer3 indexer = new ShiftGridIndexer3(bounds.Min, cellsize); 

Bitmap3 bmp = new Bitmap3(new Vector3i(numcells,numcells,numcells));
foreach (Vector3i idx in bmp.Indices()) {
    Vector3d v = indexer.FromGrid(idx);
    bmp.Set(idx, spatial.IsInside(v));
}

View fullsize

Basically the same code as above, the main difference is that we have to create a ShiftGridIndexer3 to map between grid coordinates and 3D space. In this example we only need to go from the grid (i,j,k) to 3D (x,y,z), using FromGrid(). However if in your application you want to map from 3D coordinates into the grid, you can use ToGrid(). There are also more advanced Indexer options, for example if your object has a full 3D position (origin + rotation), you can use a FrameGridIndexer3 to do the mapping.

This code uses a smaller grid resolution - 32 - so the result is blockier, as you can see on the right. There are not a lot of benefits to using the mesh IsInside() in this context, however you might find the code above useful if you have some kind of geometry that is hard to get into the level set format.

Voxelization with the Mesh Winding Number

There is a third function we can use to determine inside/outside of a mesh at a point, that is pretty awesome. Here is the code:

spatial.WindingNumber(Vector3d.Zero);  // seed cache outside of parallel eval
Bitmap3 bmp = new Bitmap3(new Vector3i(numcells+2, numcells+2, numcells+2));
gParallel.ForEach(bmp.Indices(), (idx) => {
    Vector3d v = indexer.FromGrid(idx);
    bmp.SafeSet(idx, spatial.WindingNumber(v) > 0.5);
});

Ok, the main thing is that we are using DMeshAABBTree3.WindingNumber(), which computes a hierarchical evaluation of the Mesh Winding Number. This is something that was just recently invented, and published in a SIGGRAPH paper in 2013 by Alec Jacobson, Ladislav Kavan, and Olga Sorkine-Hornung. If you have ever used the Polygon Winding Number to check if a point is inside a polygon, this is the same thing, but for 3D meshes. You just compute a simple function over the mesh triangles, and if the mesh is closed, you get an integer if you are inside the mesh, and 0 if you are outside. Kind of amazing.

The function DMesh3.WindingNumber() will do this computation, and for small meshes or single queries (eg like checking if a single 3D point is inside a mesh in a VR user-interface), this is sufficient. However if the mesh is large and/or you are doing lots of queries (like to fill a 64^3 voxel grid), it is too slow. However there is a neat trick to do a hierarchical computation based on a bounding-box tree, which is implemented in DMesh3AABBTree, and that's what I'm using above (see the paper for more details).

Since each voxel is independent, we can trivially parallelize this evaluation. The WindingNumber() function in DMesh3AABBTree does a precomputation the first time it is called, so the first line does one evaluation to seed this cache. Then we use gParallel.ForEeach, which does a multi-threaded iteration over the IEnumerable we provide (here the indices of the grid), and calls the lambda function for each index. Note that we also use Bitmap3.SafeSet() (instead of Set), which internally uses a SpinLock to make sure we aren't writing to the Bitmap3 from multiple threads. This is necessary because internally a BitArray is used, which stores the bits packed into 32-bit integers. Since we cannot read-and-flip bits independently in an atomic operation, we might end up with race conditions without the lock.

Ok, enough of that - why bother with this much more expensive computation? Because it is magic. Below is another example, where I have cut a few large holes in our venerable bunny. Also, that sphere stuck on it's back, is in fact only half a sphere, that is just overlapping - it is not connected to the bunny mesh. Look what happens when we use IsInside() (middle) or the SDF version (right). In both cases, those open boundaries are a disaster. 

View fullsize

View fullsize

Now, the interesting thing about the Mesh Winding Number (MWN) is that unlike the binary IsInside(), or the distance-field-based SDF, it is a real-valued computation that is well-defined over space. If the mesh is closed the MWN is an integer, but when the mesh contains holes, the winding number smoothly diffuses around the open boundaries. As a result, we can use a non-integer threshold to determine the range of MWN values we consider to be "inside". In the code above I used > 0.5, which produces a great result shown below-left. This value is important though - if I use 0.8, I get the result on the right - not a catastrophic failure, but there are still clearly big chunks missing. 

View fullsize

The Mesh Winding Number is a very powerful tool, and is also extremely simple to implement - my brute-force implementation is about 20 lines of code (the hierarchical version is harder, but not /that/ hard). The hierarchical evaluation is critical if you want to fill a grid. On my 6-core/12-thread machine, in Release build, computing the 64^3 voxelizations above takes a second or two. With the non-hierarchical version, it took well over a minute.

So, go forth and voxelize!

[Update] A reader asked about splitting up a mesh into 64k chunks, which is a hard constraint in the Unity Mesh class. There is a way to do this for any DMesh3, but that's a topic for a future tutorial. The VoxelSurfaceGenerator has a field MaxMeshElementCount, if you set this to 65535, then once the growing mesh hits that many vertices or triangles, a new mesh will be started. The resulting meshes will be accumulated in the VoxelSurfaceGenerator.Meshes List.

[Second Update] If you want to try using the Mesh Winding Number to repair a mesh, my new tool Cotangent uses this algorithm to repair meshes in the Solidify Tool. However it doesn't produce chunky voxels, it produces a smoother surface.

Merging Meshes with Signed Distance Fields

Left: lots of overlapping spheres, YOUR SLICER's NIGHTMARE
Right: a single continuous surface OF ULTIMATE PRINTABILITY

[Update July 6, 2018] My new tool Cotangent exposes the mesh-to-SDF-to-mesh operation I describe below in the Solidify Tool, if you want to try it without writing C# code! [/EndUpdate]

In this tutorial I'll show you how to use a few of the tools in geometry3Sharp to create solid approximations to an input mesh. We'll create a Signed Distance Field (SDF) approximation for an input DMesh3, and then use MarchingCubes to extract a new mesh from the SDF. These basic techniques can be used for an enormous number of cool things, from voxelizing and mesh repair (similar to the Make Solid tool in Autodesk Meshmixer), to data structures for spatial queries, and even for 3D modeling things like Mesh Booleans.

As a teaser, by the end of this tutorial, I'll have explained how to turn that mess of overlapping spheres on the right into a closed surface that you could safely send to any 3D printing software.

By the way, if you would like to experiment with g3Sharp, it's now available as an official NuGet package - you can find it by searching for "geometry3Sharp" in your favorite package manager.

I'll start with a basic code sample and then we'll step through it:

DMesh3 mesh = StandardMeshReader.ReadMesh("c:\\demo\\bunny_solid.obj");

int num_cells = 128;
double cell_size = mesh.CachedBounds.MaxDim / num_cells;

MeshSignedDistanceGrid sdf = new MeshSignedDistanceGrid(mesh, cell_size);
sdf.Compute();

var iso = new DenseGridTrilinearImplicit(sdf.Grid, sdf.GridOrigin, sdf.CellSize);

MarchingCubes c = new MarchingCubes();
c.Implicit = iso;
c.Bounds = mesh.CachedBounds;
c.CubeSize = c.Bounds.MaxDim / 128;
c.Bounds.Expand(3 * c.CubeSize);

c.Generate();
DMesh3 outputMesh = c.Mesh;

StandardMeshWriter.WriteMesh("c:\\demo\\output_mesh.obj", c.Mesh, WriteOptions.Defaults);

That's it. If you run this code on this solid bunny mesh, then open the input and output meshes, you'll see that they look quite similar. The SDF version is a bit smoother in some places, and it has more triangles so the shading is different. But if you overlay the two, you'll see that they solid is a very close approximation (right image).

View fullsize

Lets step through the code. After loading in the mesh, I first decide on num_cells. This defines the density of the grid we will compute the SDF on. Larger numbers mean better shape approximation, but also more memory and computation time. Internally, the SDF will be based on a dense 3D grid of floats - think of a solid block of Minecraft voxels. Each block is a cube cell_size wide.

Next we create the MeshSignedDistanceGrid object for the mesh and compute the result, which comes out in sdf.Grid. Then we create a DenseGridTrilinearImplicit based on this grid. This class will use trilinear interpolation to turn the discrete grid values (ie the blocky cubes / voxels) into a continuously-varying 3D scalar field. So, based on our Signed Distance Grid, we have created a Signed Distance Field.

We can call iso.Value(Vector3d) at any point in space, and it will return the (approximate) signed distance to the (approximated) mesh surface. If the distance is negative, then that point is inside the surface. Positive is outside, and if the value is zero, then the point is on the surface (this surface is known as the iso-surface). Of course we rarely get to exactly zero, but if we had point A just inside the surface (ie negative), and point B just outside (positive), then we know that at some point on this line, the function will evaluate to zero. So, we can do root-finding along this line, using something like Bisection or Newton's method, to converge on the zero value (wikipedia). 

This is exactly how we will get a mesh back out of our SDF. Remember, at this point our SDF is completely decoupled from the original mesh. All we have is the function iso.Value(). So what we are going to do is fill a bounding-box with smaller boxes, and evaluate the SDF at the corners of all the boxes. Then when we find a box where some corners are inside and some are outside, we know the surface cuts through that box. We'll do root-finding along the box edges to (approximately) find the zeros, and then make a patch of triangles. This is the famous Marching Cubes algorithm. Paul Bourke has an excellent page with more information, and you can find a PDF of the original paper here - compared to a modern SIGGRAPH paper it is incredibly readable.

In g3Sharp the MarchingCubes class implements this method, and you can give it an arbitrary function to surface via the Implicit member. This way of representing a 3D shape - as a scalar function over space - is often called an Implicit Surface, hence the naming. We also have to provide a bounding box to search inside of (ie to fill with smaller cubes), and the CubeSize we wish to use. Note the small expansion of the bounds - if you don't do this, the most extreme edges of the shape might be clipped off (3 cells is probably overkill).

After calling Generate(), the mesh is built and we can write it out. Easy!

You're not impressed? Ok, how about this one. Here's the same bunny with an intersecting sphere stuck on it, and I did a bit of sculpting to create a self-intersection (download). If you wanted to turn this into a solid non-self-intersecting shell (say, to 3D print it), well, you're in trouble. These are hard problems to solve. But not for an SDF - run this file through the code above, and the output mesh is a closed, manifold shell. The trade-off for this simplicity is that we have to accept some resampling artifacts around the sharp edges.

View fullsize

(click to enlarge)

In the examples above, what is "inside" vs "outside" is defined by something called the winding number. We'll explore this concept more in a future post. But, basically, in this context it means that for any given point in space, we can count up how many "times" the point is inside the input surface. So, points inside both the sphere and the bunny, have winding number 2. Similarly, points inside that bit that is self-intersecting (which you can't see) also have winding number 2 - they are inside the bunny "twice". Points outside have winding number 0.

But what about cavities on the inside of the surface? Well, the winding number depends on the orientation of the mesh. If we flip a mesh inside-out, then the points inside it have negative winding numbers. In the SDF mesher, we will define any point with positive winding number as inside. This means we can use inside-out meshes to define holes, and also to do Boolean subtraction. Here's an example below. I am using Meshmixer to view the output meshes, and in Meshmixer the red/white stripey pattern means you are looking at the "back-side" of the mesh surface. I cut away in the SDF+MC mesh to show that there is also a fully-enclosed hole.

View fullsize

click to embiggen

In the description above, I mentioned two parameters - the cell_size we passed into MeshSignedDistanceGrid, and the MarchingCubes.CubeSize. The cell_size of the Signed Distance Grid defines how accurate our approximation of the input mesh can be. Even if we mesh at a very high resolution, if the grid doesn't capture the shape well, we'll have approximation error.

In the image below, I set num_cells to 16, 32, 64, 128, and 256, and used a CubeSize of 128. At the lower resolutions we clearly don't have enough values in the grid to capture the shape. However it is quite interesting to mesh a low-resolution grid at high resolution. The trilinear interpolation produces a smoothly-varying patch inside each cell, but you can clearly see the discontinuities at the cell boundaries, where the interpolation is only C0 continuous. At the higher 128 and 256 resolutions, the grid is as or more accurate than the Marching Cubes triangulation, so you don't see any difference.

View fullsize

click for big

Varying the CubeSize is not so nice at lower resolutions - again I went from 16-256 below, this time with num_cells=256 for the SDF grid. The only reason you might use lower-resolution marching cubes is to reduce memory (Marching Cubes will produce huge meshes very quickly!). At the highest resolution below, you can start to see the original triangles - clearly our SDF approximation is quite accurate in this case! However even at this resolution, the sharp edge around the border of our intersection is not particularly clean. This is caused by both the SDF and the Marching Cubes, but even if it were a nice, smooth sharp edge in the SDF, Marching Cubes will not be able to capture it.

View fullsize

bigbig

View fullsize

So, to capture shape details we want to use high MC resolutions, but then we end up with huge meshes. What  to do? Use another tool in our mesh processing toolbox, of course. The Reducer class, which I described in a previous tutorial, can help us get back to reasonable mesh resolutions. In this case you only need a few lines:

Reducer r = new Reducer(outputMesh);
r.ReduceToTriangleCount(50000);

In the 256-SDF-grid, 256-MC-grid case above, the initial MC mesh has about 450k triangles. The code above will reduce this mesh to 50k triangles. This takes about 3 seconds on my 4-core desktop computer. This is actually more time that it takes to generate the 450k mesh in the first place! The result, shown in the middle on the right, is much lower-density but clearly there is still a lot of redundant geometry. If we go further, down to 10k triangles (far right), the mesh starts to get better.

View fullsize

You'll also notice that in the 10k-triangles version, the sharp edge around the intersection has started to get a bit cleaner. I have (experimentally) found that using a slight modification to the Reducer setup will do an even better job at recovering these sharp edges. Instead of reducing to a specific triangle count, the Reducer also supports reducing to a target edge length. The following code:

r.ReduceToEdgeLength(2*c.CubeSize)

resulted in the mesh on the right, which has a very crisp sharp edge around where the sphere was subtracted. This doesn't always work, but it does work sometimes! 

So, we can combine a multiple overlapping meshes into a single SDF solid, mesh it at a crazy high resolution, and then use Mesh Simplification to get it back to a closed shell we could actually use in other software. And maybe even get sharp edges out. What to do? Generate some shapes, of course! Geometry3Sharp has lots of different kinds of Mesh Generators built in - Spheres, Cylinders, Boxes, Tubes, Surfaces of Revolution, and more. Look in the mesh_generators/ folder to find all the generator classes. You can do procedural shape generation in two steps - first generate a bunch of small closed meshes, then combine them all and send through the code above. It literally is that easy.

As an example, here is a bit of code that generates a new mesh from an input mesh, by adding a sphere for each vertex, and a rectangular box along each edge:

Sphere3Generator_NormalizedCube gen = new Sphere3Generator_NormalizedCube() { Radius = sphere_radius, EdgeVertices = 5 };
DMesh3 sphereMesh = gen.Generate().MakeDMesh();

DMesh3 latticeMesh = new DMesh3();
MeshEditor editor = new MeshEditor(latticeMesh);
foreach ( int vid in mesh.VertexIndices() ) {
    DMesh3 copy = new DMesh3(sphereMesh);
    MeshTransforms.Translate(copy, mesh.GetVertex(vid));
    editor.AppendMesh(copy);
}
foreach ( Index4i edge_info in mesh.Edges() ) {
    Vector3d a = mesh.GetVertex(edge_info.a), b = mesh.GetVertex(edge_info.b);
    Frame3f f = new Frame3f((a + b) * 0.5, (b - a).Normalized);
    editor.AppendBox(f, new Vector3f(box_width, box_width, (b - a).Length*0.5));
}

I set the sphere_radius and box_diam to something appropriate for the scale of my mesh, and ran it on a bunny reduced to 512 triangles, with the SDF-grid cell_size and Marching Cubes CubeSize both set to 512. This crazy resolution is required to capture the fine details. After about 30 seconds, the set of overlapping meshes on the left is turned into the single solid on the right:

View fullsize

You really want to click on this one!

Hopefully this gives you some ideas =)

One caveat about Marching Cubes should be mentioned, and is illustrated in the low-res MC image further up the page. I mentioned that we figure out the mesh patch that should be inside each "cube" based on whether the corners of the cube are inside or outside the surface. Most of the time, this works well, but there are cases where it is ambiguous. Currently, the Marching Cubes implementation in g3Sharp does not properly handle these cases. It is mostly a problem when the shape varies much more rapidly than the MC mesh. In our case these failures will leave small holes in the mesh, as certain triangles will be discarded (in other implementations these triangles would produce non-manifold geometry, but DMesh3 doesn't allow that). We'll be fixing this in the future.

To give credit where credit is due, the super-fast Mesh to SDF conversion I have implemented in g3Sharp is based on a C++ implementation by Christopher Batty, which is on github. And he tells me this code was a cleaned-up version of an initial implementation by Robert Bridson. My C# version has been extensively refactored and modified so that some steps can be multi-threaded. I also added parity-counting to properly handle overlapping shells. 

Mesh Simplification with g3Sharp

[Update July 6, 2018] If you would like to test this Reducer implementation without writing C# code, you can try it in my new tool Cotangent, in the Simplify tool [/EndUpdate]

Recently a user posted a github issue asking for a mesh simplification example. It just so happened that I had recently finished writing an implementation of Garland and Heckbert's Quadric Error Metric (QEM) Simplification algorithm. If you want to learn more about this technique, the original papers and several later articles are available on Michael Garland's Website, and are very readable. I will give the broad strokes below, but first here is an example of what we are talking about - automatic reduction of a bunny mesh from 13,000 to 500 triangles:

View fullsize

An easy way to Simplify or Reduce a mesh (which is the terminology I use, because...well I don't have a good reason, but it's how I think of it!) is to iteratively collapse edges in the mesh. Each collapse removes one edges and the two (or one at the boundary) triangles connected to that edge, as well as one vertex. Just repeat until you hit your target triangle count, and you're done. Easy! 

Except, which edge should you collapse first? And, when you collapse the edge, should you just keep the existing vertex position? In most cases it would at least make more sense to move the remaining vertex to the edge midpoint. But could we do better? This is where QEM comes in. Basically, the Quadric Error gives us a way to (1) "score" edges, so we know which edge collapses will have the smallest impact on the shape, and (2) predict a position for the new vertex that will minimize the score after the collapse. 

Ultimately, the Quadric Error is a measurement of the sum-of-distances from a point to a set of planes. If you think of the ring of triangles around a vertex, each triangle makes a plane.  The distance from the vertex to that plane is zero. But if we start moving the vertex, this distance increases. So we can "score" an a vertex movement (like an edge collapse) by measuring all the distances from the new vertex to all the input planes (of the original triangles). Each point-plane distance measurement can be expressed as a matrix multiply with the point, and since Ap+Bp = (A+B)p, we can combine all the error measurements into a single matrix multiplication!

Even better, after an edge collapse, we can think of that vertex as having a total error measured relative to the input planes of both vertices (still just one matrix). So as we do sequential collapses, we accumulate all the plane-distance-functions of the original mesh triangles that were (at some point in the past) connected to the remaining vertex. And it's still just one matrix. In the '99 paper linked from the site above [PDF], Garland showed how the QEM error is in some sense a measure of surface curvature, and produces "optimal" triangulations, under a reasonable definition of optimal. Amazing!

But, ok, you're probably just here for the code, right? To use the g3sharp implementation you need to get your mesh to be a DMesh3, see my previous tutorial for how to do that. Then you just need a couple lines to create a Reducer object and run the simplification:

DMesh3 mesh = load_my_mesh_somehow();
Reducer r = new Reducer(mesh);
r.ReduceToTriangleCount(500);

In the code above, 500 is the target triangle count. This takes a fraction of a second to run. I have not done extensive profiling, but on a relatively fast machine I can reduce a 350k mesh to 100k in 2 to 3 seconds. So, it's pretty fast.

Mesh Validity Checking

Most of the mesh processing algorithms in g3Sharp require that the input meshes be manifold. This term has lots of meanings, in this context it means that at minimum each mesh edge is connected 1 or 2 triangles. Inside DMesh3, edge triangles are stored in an Index2i object, so DMesh3 can't even represent a non-manifold edge. In most cases we also require that there are no bowtie vertices, which are vertices connected to disjoint sets of triangles. The simplest example of this would be two triangles connected only at one vertex (hence the name "bowtie"). 

If these conditions are not met, then some mesh operations - like an edge collapse - can produce undefined results, result in exceptions, and so on. So, to test that your mesh is internally consistent, you can use the DMesh3.CheckValidity() function. You can configure this function to have different behavior if the mesh is not valid, ie it can assert, throw an exception, just return false, and so on. By default it will consider bowtie vertices to be invalid, but you can also configure this behavior with the bAllowNonManifoldVertices argument. 

Note that this function also does very thorough testing of the internal mesh data structures to make sure everything is consistent. So, it is relatively expensive, and you probably do not want to be calling it all the time in production code. One exception is when loading meshes from a file, in that case you really should check the meshes after reading, it can save you a lot of headaches trying to track down garbage-in/garbage-out type problems!

Preserving Boundaries

In some cases, for meshes with boundaries you might need to preserve the boundary loops exactly. For example if you are actually reducing a sub-region of a larger mesh, or a mesh split along UV boundaries. This just takes a few more lines, before your call to ReduceToTriangleCount():

r.SetExternalConstraints(new MeshConstraints());
MeshConstraintUtil.FixAllBoundaryEdges(r.Constraints, mesh);

The MeshConstraints object in the code above is in fact a very powerful facility, that allows you to constrain much more than just boundary edges. But that is a topic for a future tutorial. You can poke around the data structure, or the MeshConstraintUtil helper class, to find out more. The images below compare reducing a bunny-with-boundary to 500 triangles without (left) and with (right) a preserved boundary. 

View fullsize

Here is a closeup of the boundary around the bunny's front paws. You see on the left that there are significantly shorter edges along the boundary loop, because it has been exactly preserved. However, you might also note if you look closely (or click to enlarge) that on the front-left paw that there are some thin sliver triangles. This is a current limitation of boundary preservation - it may result in a bit of ugly stuff at the border. This will hopefully be improved in future updates.

Project to Target

Finally, one last thing that you might want to do when Simplifying a mesh. By default, the "new" vertex position after an edge collapse is computed by minimizing the QEM error for that vertex. Compared to something like edge midpoints, this produces nicer shapes and actually results in the algorithm running much faster. However in some cases you may require that the vertex positions lie on the original mesh surface. This is also supported. First you build a spatial data structure, like the DMeshAABBTree3 we built in the Spatial Query tutorial, and then set that as a "Projection Target" for the Reducer. This causes the vertex positions to be mapped to the nearest points on the input mesh surface. Here is the code:

DMeshAABBTree3 tree = new DMeshAABBTree3(new DMesh3(mesh));
tree.Build();
MeshProjectionTarget target = new MeshProjectionTarget(tree.Mesh, tree);
r.SetProjectionTarget(target);
r.ProjectionMode = Reducer.TargetProjectionMode.Inline;

The last line is optional. This causes the Reducer to compute the projection each time it wants to evaluate the QEM error for that vertex. This is "more correct" but many of these vertices will eventually be discarded, so the work is in some sense wasted (projections are expensive). If you leave this line out, then the projection is computed after the reducer is finished, for just the vertices that were ultimately kept. The image below compares no projection (left) and with inline projection (right), overlaid on the original surface (dark grey). The simplified meshes don't actually look very different, but you can see that on the right, most of the mesh is "inside" the original surface, while on the left it is roughly half-and-half inside/outside.

One thing to keep in mind with Projection is that for thin parts, the projection can easily end up on the "wrong" side. So, for most simplification problems you probably don't need it. Which is great because it's quite a bit slower!

Now, go save some triangles! Next up is Remeshing, which works in much the same way, only it's also much more complicated...